PSİKROMETRİ – I – Bölüm 1 – Başlık 2 – KURU VE NEMLİ HAVANIN TERMODİNAMİK ÖZELLİKLERİ

2. KURU VE NEMLİ HAVANIN TERMODİNAMİK ÖZELLİKLERİ

2.1 Giriş

Atmosfer azot, oksijen, küçük miktarlarda başka gazlar, su buharı ve duman, polenler, ve havayı kirleten atık gazlardan oluşmaktadır.  Bu karışım bazı kitaplarda “atmosferik hava” veya “nemli hava” olarak adlandırılmaktadır. Biz kitabımızda “atmosferik hava” tabirini hiç kullanmayacağız. Çünkü bu tabir Dünya’mızın tamamını saran, troposfer ve stratosferden oluşan hava kütlesine de verilen isimdir. Halbuki psikrometri yalnızca troposferin alt seviyelerindeki hava ile ilgilenmektedir. Bu nedenle yanıltıcı olabileceğini düşündüğümüz “atmosferik hava” tabiri yerine “hava” tabirini kullanacağız. Bu tabiri “nemli hava”, “kuru hava” ve “su buharı” olarak genişletebiliriz. “Nemli hava”  havadan içerdiği iki elemanla ayrılmaktadır. Bunlar “kuru hava” ve “su buharı”ndan oluşmaktadır. Kuru hava ise içindeki su buharından, havayı kirleten duman, polen ve atık gazlardan arındırılmış teorik bir kavramdır.

Psikrometrinin üzerinde çalıştığı eleman havadır ve bu hava daima iki komponentin, su buharı ile kuru havanın karışımından oluşmaktadır. Bu karışım oranı sabit olmayıp , kuru termometre sıcaklığı, deniz seviyesinden yükseklik gibi şartlara bağlı olarak değişiklik göstermektedir.

2.2 Kuru havanın yapısı

Birinci komponent olan kuru hava hacimsel olarak %78 Azot, %21 Oksijen, %1 Argon, küçük ve değişik oranlarda asgari sekiz ayrı gazın oluşumundan oluşmaktadır.

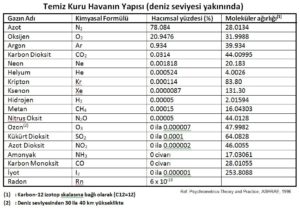
Yukarıdaki tabloda adı geçen gazların tamamı kendi kritik sıcaklıklarının çok üstündedirler. Bu gazların normal atmosferik şartlarda -100^oC ortam sıcaklığının üstünde yoğuşmaları, havayı oluşturan karışımdan ayrılmaları , dolayısıyla havanın oluşumunda bir değişiklik olması söz konusu değildir. Bu nedenle kuru hava tek bir gaz gibi mütalaa edilebilir, psikrometrik proseslere ve psikrometrik tablonun oluşumuna yönelik hesaplara esas alınabilir. Çünü yıllardır yapılan araştırmalar havanın karışımında ve dolayısıyla moleküler kütlesinde çok küçük değişikliklerin olduğu ve bu değişikliklerin psikrometrik değerlerin oluşumunda çok az etki yarattıkları tespit edilmiştir. 1983 yılında Hyland ve Wexler 28.9645 kg/kmol değerini, 2001’de de Nelson ve Sauer 28.95849 kg/kmol’ü havanın molar kütlesi olan olarak hesaplamışlardır. Bizim verdiğimiz “Temiz Kuru Havanın Yapısı” tablosundaki değerler kullanıldığında ise 28.964 kg/kmol bulunmaktadır.

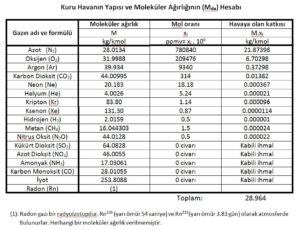
Hesap tarzı aşağıdaki formülde gösterilmiştir.

∑M.x_i= M_N2.x_iN2+ M_O2.x_iO2+ …… + M_I2.x_iI2       ………………. (kg/kmol)

Yukarıdaki tablonun oluşumunu daha iyi anlayabilmek için kullanılan tabirlerin açıklanması gerekmektedir. Bunlardan ilki moleküler ağırlık ve gaz sabitesidir.

2.2.1. Mole (Mol) ve Moleküler Ağırlık:

Mol ve moleküler kütle, bir maddenin (kitlenin yapısına bağlı olarak ve hangisi daha uygunsa) gram-atom veya gram-molekül ağırlığı, 12 gram karbon izotopundaki atom sayısı kadar temel yapıtaşı içeren bir sistemin madde miktarıdır. Temel yapıtaşları atom, molekül, iyon, elektron ve benzeri taneciklerden oluşan gruplar olabilir ve mol kullanılırken belirtilmelidir. Diğer bir anlatımla Bir mol ağırlığındaki bir maddenin kütlesel ağırlığı 6.022×10²³molekül içermektedir. Bu sayı Avogadro Sayısıolarak bilinmektedir. Bir mol da karbon 12 gram ağırlığındaki Karbon 12 örneğinde bulunan atom sayısı olarak ta tarif edilmektedir.

Önceleri 16 olarak kabul edilen oksijen izotopunun ağırlığı esas alınıyordu. Ancak oksijenin değişik izotoplara sahip olması nedeniyle bu sistem terk edildi. 159/60 yıllarında Uluslararası Teorik ve Uygulamalı Fizik Birliği (IUPAP) ile Uluslararası Teorik ve Uygulamalı Kimya Birliği (IUPAC) karbon izotopunun kullanılması konusunda anlaştılar. Her iki kuruluş kütle numarası 12 olan karbon elementi izotopunun (Karbon-12, C¹²) atom ağırlığı, yani atom kütlesi tam olarak 12 olan bu izotopun esas alınması konusunda anlaştılar. Böylece tüm elementler için birleştirilmiş bir bağıl atomik kütlr skalası belirlenmiş oldu.

2.2.2. Mol Oranı:

“x” ile gösterilen mol oranı bir karışımda bulunan bir gazın mol miktarının o karışımda bulunan tüm gazların mol miktarlarının toplamına bölünmesi ile elde edilen sayıdır. Örneğin iki elemanlı bir karışımdaki birinci elemanın mol oranı aşağıdaki gibidir:

x₁=n₁/(n₁+ n₂)

Burada “n₁” ve “n₂” karışımı oluşturan elemanların her birinin mol miktarlarıdır. Bir gaz karışımını oluşturan eleman sayısı kaç olursa olsun mol oranlarının toplamı daima 1’e eşittir.

x₁+x₂+…………….. x_n= 1

2.2.3. Üniversal Gaz Sabiti:

Universal gaz sabiti ideal bir gazın basıncıyla hacminin basıncıyla çarpımının mutlak sıcaklığa bölünmesiyle elde edilen değerdir. Diğer bir deyişle, basınç ile hacmin çarpımının mutlak sıcaklığa olan oranıdır.

P.V= R . T

“R”  ile gösterilen bu sabite bütün gazlar için geçerli olup değeri:               

8.31441 kJ/(kg.mol.^oK)’dir.

2.2.4. Kuru Hava ve Su Buharının Gaz Sabitleri:

Herhangi bir gazın gaz sabiti, üniversal gaz sabitinin o gazın moleküler ağırlığına bölünmesi ile elde edilir.

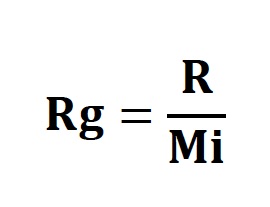 Bu duruma göre azot, oksijen ve kuru havanın gaz sabitleri şu şekilde bulunur:

2.2.5. İdeal Gaz Karışımları :

İdeal gaz karışımları ile ilgili iki temel kanunu hatırlamakta büyük yarar vardır. Bu kanunlar:

• Dalton’un toplanan basınçlar kanunu ve
• Amagat’ın toplanan hacimler kanunu’dur.

Dalton Kanunu’na göre bir gaz karışımının basıncı, karışan gazların karışım sıcaklığında olmaları ve ayrı ayrı toplam hacmi kaplamaları durumunda sahip olacakları basıncın toplamıdır. Amagat Kanunu’na göre de bir gaz karışımının hacmi, karışan gazların karışım sıcaklığı ve basıncında olmaları durumunda yarı ayrı kaplayacakları hacimlerin toplamıdır.

2.3 Su buharı

Psikrometriyi tam olarak anlayabilmek için için H₂O olarak ifade edilen suyun katı, sıvı ve gaz halindeki özelliklerini bütünüyle bilmek gerekir. Birçok madde de olduğu gibi su da üç fazda bulunmaktadır: katı (buz), sıvı (su) ve gaz (buhar veya su buharı). Suyun en büyük özelliği bu her üç fazın da günlük yaşamımızda görülebilmesi ve izlenebilmesidir. Örneğin Yazın bir bardak suya birkaç küp buz koyduğunuzda iki fazı bir arada izlersiniz. Bir müddet sonra bardağın dış sathında su zerrecikleri belirmeye başlar. Bu da yoğuşmakta olan su buharıdır. Bunun nedeni de bardağın dış sathının yoğuşma sıcaklığının altındaki bir sıcaklığa kadar soğumuş olmasıdır. Daha ilerideki bahislerde detaylı olarak ele alacağımız bu konu ile ilgili olarak kısaca şunu söyleyebiliriz: Normal atmosferik şartlarda (STP, Deniz seviyesi, 101.325 Pa basınç) hava içinde bulunabilen maksimum su buharı kuru termometre sıcaklılığna bağlı olarak değişiklikler gösterir. Sıcaklık düştükçe hava içinde bulunabilecek su buharı miktarı azalmaktadır. Bunu da yukarıda bardak örneğinde gördüğümüz gibi satıh yoğuşması ile kendini belli etmektedir. Atmosferik olaylarda ise bu durum kendini yağmur ve kar yağışı olarak belli eder.

Aşağıdaki diyagramda, beher kilogram kuru hava içinde bulunabilecek maksimum su buharı miktarı kilogarm olarak gösterilmektedir.

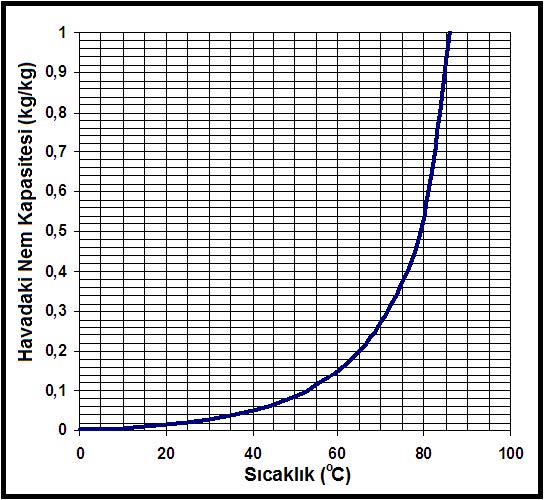
Suyun faz değişiklikleri termodinamik açıdan büyük önem taşır. Katı halden sıvı hale, buzdan suya dönüşmesine “erime” deriz. 0^oC sıcaklıktaki buzun aynı sıcaklıktaki suya dönüşmesi için gerekli ısı ilavesi 333.47 kJ/kg’dır. Bu işlemin tersi de mümkündür buna da donma deriz.

Keza aynı şekilde suyun sıvı halinin gaz haline, suyun buhar haline dönüşmesi için de ısı ilavesi gerekmektedir. Bu miktar da 15^oC muhit sıcaklığında 2465.38 kJ/kg, 100^oC’ta ise 2256.47 kJ/kg’dır. Bir kilogram suyun buharlaşması  için gerekli ısı miktarı 0^oC’ta 2500.93 kJ/kg ile 100^oC’ta 2256.47 kJ/kg arasında değişir.  Su için logP-H diyagramındaki çan eğrisinin içi buharlaşma prosesini göstermektedir. Burada değişik sıcaklıklarda ve basınçlarda suyun buharlaşması için gereken ısı miktarını hesaplamak mümkündür.

Buzun hiç sıvı hale dönüşmeden gaz haline geçmesi de mümkündür. Bu işleme depozisyon tersine de sublimasyon denir. Bu işlem için gerekli olan ısı miktarı da doğal olarak 0^cC’taki erime ısısı ile aynı sıcaklıktaki buharlaşma ısısının toplamına eşittir.

                    H_sub= h_fg1 + h_fg2=333.47 + 2500.93=2834.4 kJ/kg

Burada:

                     h₌ Antalpi (kJ/kg)

                     h_fg1 = Suyun erime antalpisi (kJ/kg)

 h_fg2= Suyun buharlaşma antalpisi (kJ/kg) ‘dır.

Bu değerler aşağıdaki “Doymuş Haldeki Suyun Termodinamik Özellikleri”nde görülmektedir.

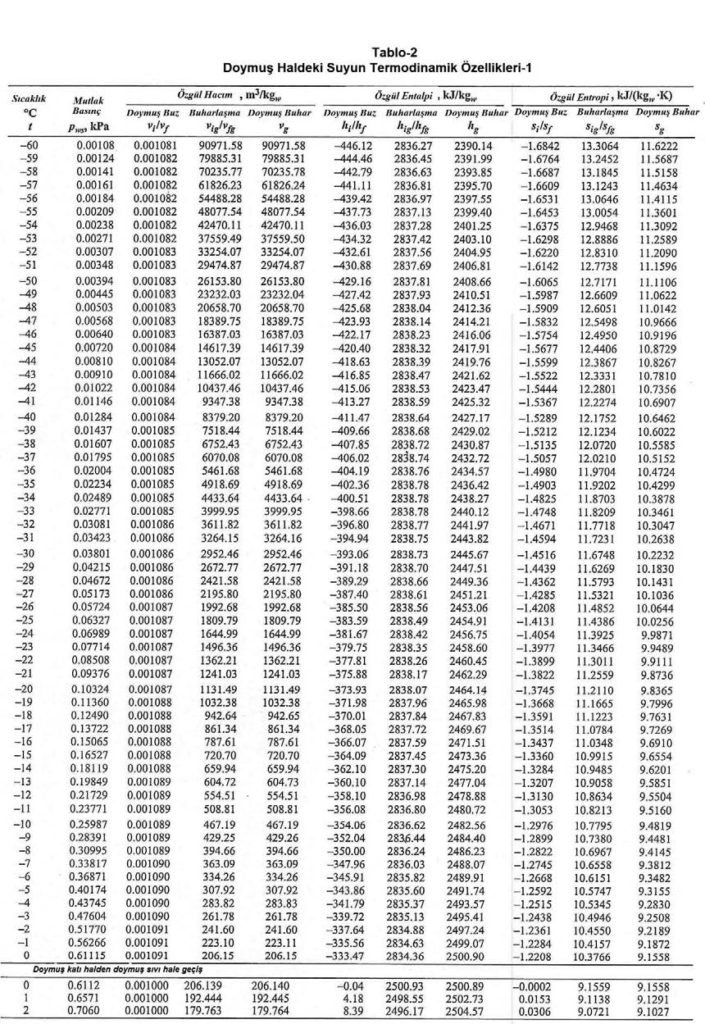
Ref: ASHRAE Fundamentals-2013

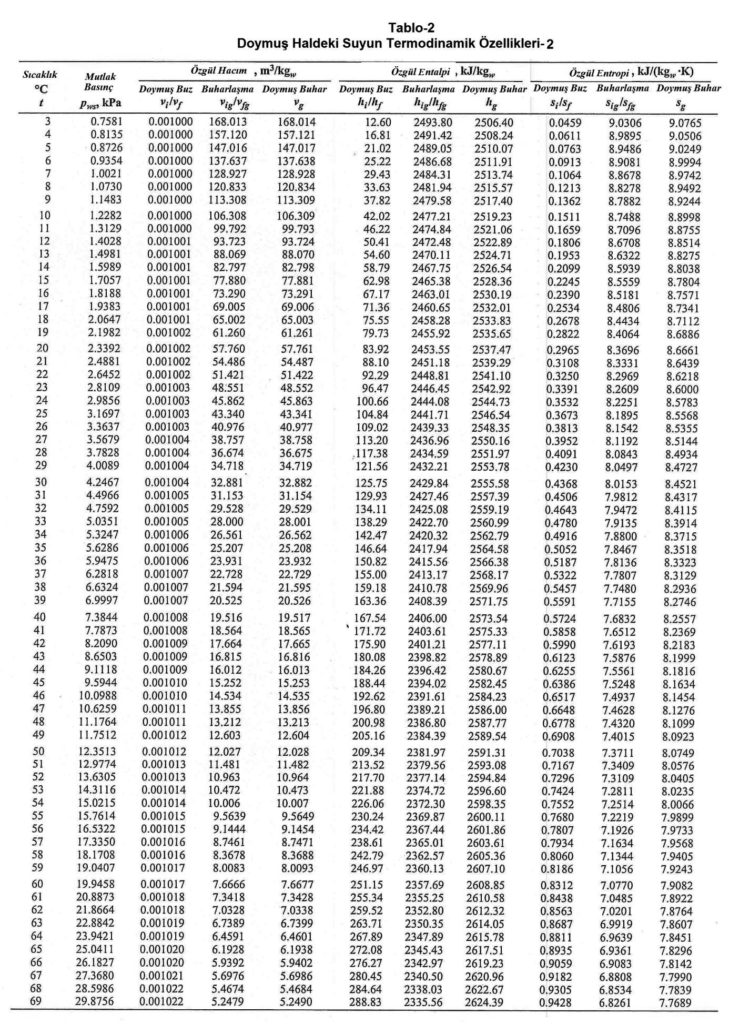
Ref: ASHRAE Fundamentals-2013

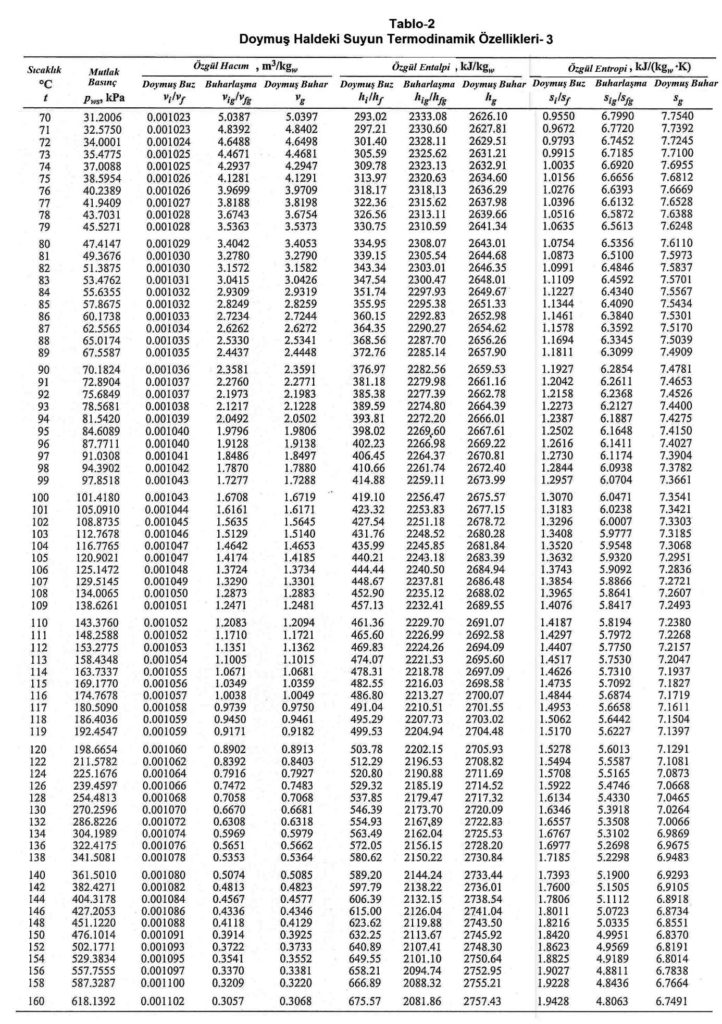
Ref: ASHRAE Fundamentals-2013

2.3.1. Su buharının molerküler ağırlığı ve gaz sabiti

Su buharı iki hidrojen ve bir oksijen atomundan oluşmaktadır. Bu gazların her birinin Karbon-12 skalasına göre moleküler ağırlıkları aşağıdaki gibidir.

M_H2= 2.0159 kg/kmol

M_O2= 31.9988 kg/kmol

M_{H20 (buhar)}= (1 x 2.0159) + ( 0.5 x 31.9988) 

M_{H20 (buhar)}= 18.01534 kg/kMol

2.4. Kuru hava ile su buharının karışımı

Nemli hava, veya bu kitapta kullandığımız tabiriyle hava su buharı ile kuru havanın ikili karışımından oluşur. Kuru havanın homojene yakın karışımına karşılık su buharı ve kuru havanın karışımından oluşan hava homojen değildir. Sıcaklık ve irtifaya göre farklılıklar gösterir.  Örneğin -40^oC’tan daha düşük sıcaklıklarda hava içindeki su buharı oranı sıfıra yakındır. Sıcaklık ve basınca bağlı olarak çok yüksek değerlere ulaşabilir.  Saturasyon veya doyma noktası gaz durumundaki su (buhar)  ile yoğuşarak sıvıya dönüşmüş sıvı (su) arasındaki dengedir.

Teknik tabir olarak yaygınca kullanılan saturasyon kelimesinin kökeni Latince “satar” kelimesidir; “dolu” veya “doyum” manasına gelmektedir. Ancak biz kitabımızda “doyma noktası”tabirini kullanacağız. Su buharı ile kuru hava atmosferde aynı hacmi paylaşmaktadır. İkisinin kısmi basınçlarının toplamı da atmosferik basıncı oluşturmaktadır.  Doyma noktası da belirli bir basınç ve sıcaklıkta birim atmosferik hacim içinde bulunabilecek maksimum su buharı molekülü miktarını ifade etmektedir. Bu  tabir de “gr_{su buharı}/kg_{kuru hava}” veya  “kg_{su buharı}/kg_{kuru hava}” olarak gösterilir.

 

2.4.1. Standart Atmosfer

Atmosferik havanın sıcaklık ve barometrik basıncı irtifa ile ve buna ilaveten mahallin coğrafik ve meteorolojik koşullarına bağlı olarak değişiklik gösterebilir. Standart atmosfer deniz seviyesinde 15^oC ve 101.325 kPa barometrik basınç olarak ifade edilmektedir. Sıcaklığın troposferde irtifaya bağlı olarak lineer bir değişiklik göstereceği, azalacağı, stratosferde ise sabit olacağı belirlenmiştir.

Aşağıdaki tabloda deniz seviyesinden olan irtifaya bağlı olarak sıcaklık ve basınç değişiklikleri gösterilmektedir.

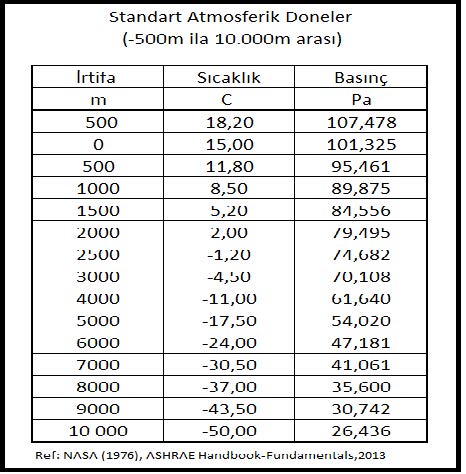
“Standart Atmosferik Doneler” tablosundaki basınç değerleri aşağıdaki şekilde hesaplanabilir:

p= 101.325 (1-2.25577 x 10^-5x Z)^5.2559……….(kPa)

Sıcaklık değerlerinin hesaplanmasında ise şu formül kullanılabilir:

t= 15 – 0.0065 x Z………………………………………(^oC)

Bu formüller 2013-ASHRAE Handbook Fundamentals’da yer almakta olup hatasız bir şekilde -5000 metre ila 11000 metre irtifa arasında kullanılabileceği belirtilmektedir.”Z” deniz seviyesinden olan yüksekliği belirtmektedir.

 

2.4.2. Havanın Termodinamik Özellikleri:

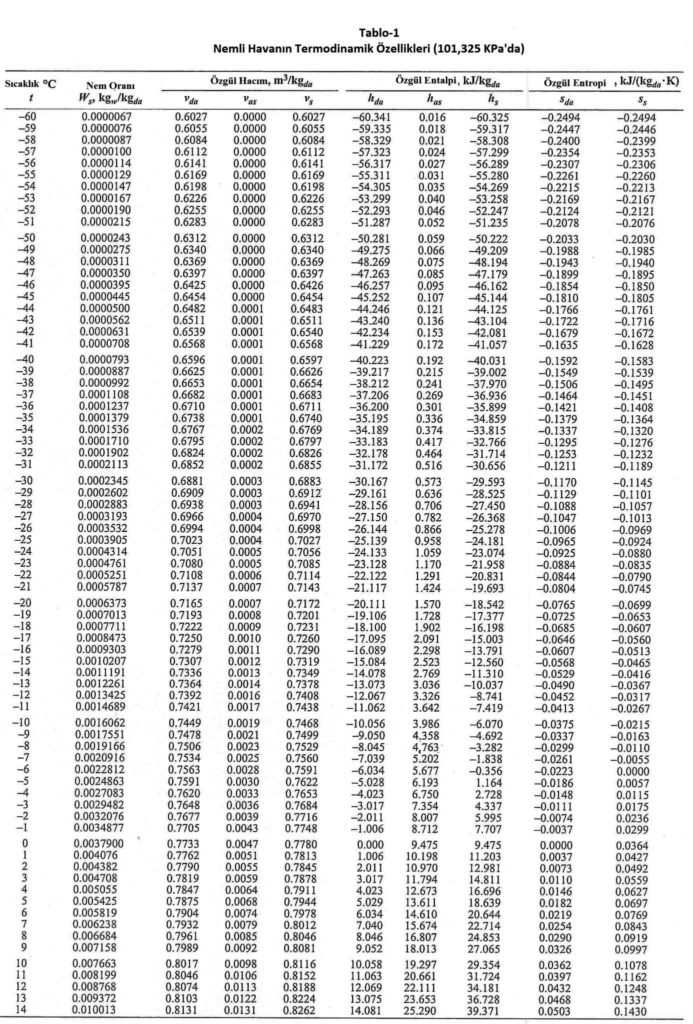
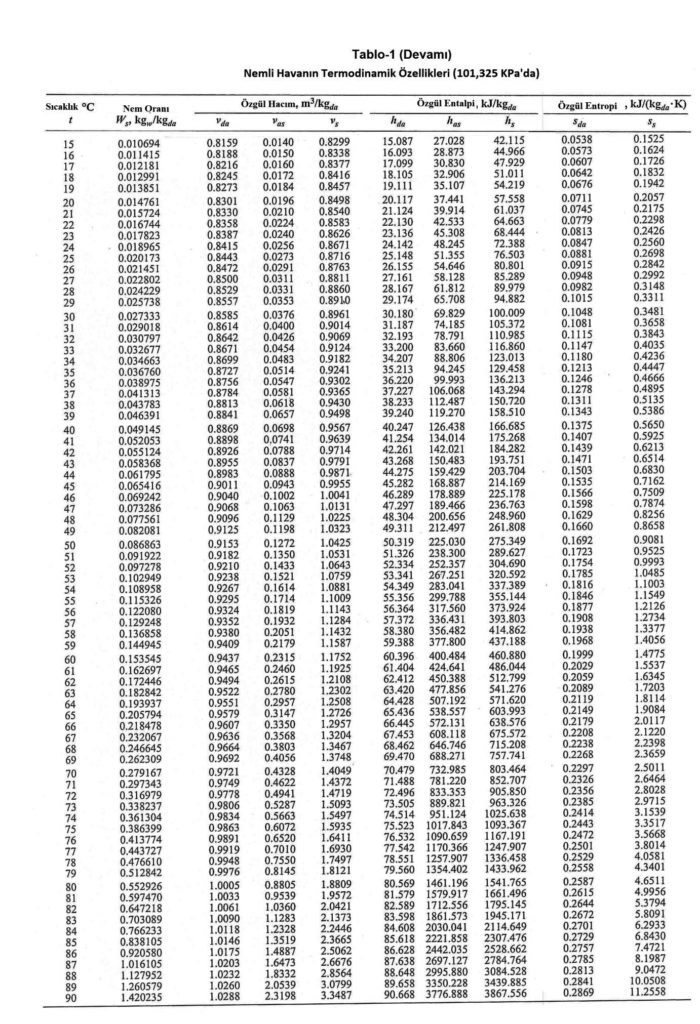
Aşağıdaki tablolarda havanın termodinamik özellikleri verilmektedir. Hermann, Kretzchmar ve Gatley  tarafından 2009 yılında yayınlanan araştırmadaki formüller esas alınarak hesaplanan havanın termodinamik özellikleri aşağıdaki tablolarda verilmektedir. Bu tabloda kullanılan birimler aşağıdadır

t= “Celcius” skalasına göre sıcaklık. “T”olarak gösterilen “Kelvin”

      skalası ile bağlantısı aşağıdaki gibidir:

    T =t + 273.15……………………… (^oK)

Ref: ASHRAE Fundamentals-2013

Ref: ASHRAE Fundamentals-2013

Tabloda kullanılan sembollerin açıklamaları da aşağıdadır:

W_s= Doyma noktasındaki su buharı miktarının kuru havaya oranı.

       “kg_w/kg_da” olarak ifade edilir.

v_da= Kuru havanın özgül hacmı  “m³/kg_da” olarak ifade edilir.

v_s   = Doyma noktasındaki havanın özgül hacmı “m³/kg_da” olarak ifade

         edilir.

v_as = Doyma noktasındaki kuru havanın özgül hacmı ile kuru havanın

        özgül hacımları arasındaki fark, “m³/kg_da” olarak ifade edilir.

h_da = Kuru havanın özgül antalpisi. “kJ/kg_da” olarak ifade edilir.

h_s  = Doyma noktasındaki kuru havanın özgül antalpisi. “kJ/kg_da” olarak

        ifade edilir.

h_as = Doyma noktasındaki kuru havanın özgül antalpisi ile kuru havanın

        antalpisi arasındaki fark, “kJ/kg_da” olarak ifade edilir.

s_da = Kuru havanın özgül antropisi, “kJ/(kg_da. K)” olarak ifade edilir.

s_s   = Doyma noktasındaki kuru hava ile kuru havanın özgül antropisi

        arasındaki fark, “kJ/(kg_da. K)” olarak ifade edilir.

2.4.3. Doyma Eğrisi ve Hesaplanması

Psikrometrik proses ve hesaplarda doyma eğrisi çok önemli bir yer işgal eder. Bu eğri aynı zamanda su buharı basıncını ve su buharı doyma sıcaklığını da belirler. Birçok eserde bu şartların belirlenmesi için ASHRAE Handbook-Fundamentals’a refere olunur ve oradaki tabloların kullanılması önerilir. Bu tablolar kitabımızda da verilmektedir. Ancak bu değerlerin hesap yoluyla da bulunabileceğinin bilinmesinde fayda vardır. Çünkü mühendislik bir şeyi olduğu gibi kabul etmek değil, bunun nedenlerini bilmek, empirik te olsa formüller ile bu değerlere ulaşabilmektir. Kullandığımız tabloların çoğu da bu yollarla hesaplanarak bulunmuştur. Buna örnek olarak kanal hesap abaklarını, ısıtma ve soğutma hidronik hesaplarında kullanılan boru hesap abaklarını gösterebiliriz.

Günümüzde en doğru yaklaşımları veren formül IAPWS (International Association for the Properties of Water and Steam) -IF97’de belirtilen formüllerdir.  Sıvı haldeki su sathı üzerindeki doyma basıncının sıcaklığa bağlı olarak hesaplanması aşağıdaki formülle belirlenmiştir.

p_ws=1000 x (2 x C/(-B+(B²-4 x A x C)^0.5))⁴………..(kPa)

Bu formülde :

A= Q²+ (N₁x Q) + N₂

B= (N₃x Q²) + (N₄x Q) + N₅

C= (N₆x Q²) + (N₇x Q) + N₈

“Q” değeri ise aşağıdaki formülle hesaplanır:

Q= T + N₉/(T-N₁₀)

T= t_C+273.15 

“t_C” Celcius skalasına göre doyma sıcaklığıdır.      (^oC)

N₁=  1167.05214527670            N₂= -724213.167032060

N₃= -17.0738469400920            N₄= 12020.8247024700

N₅= -3232555.03223330            N₆= 14.9151086135300

N₇= -4823.26573615910           N₈= 405113.405420570

N₉= -0.238555575678490         N₁₀= 650.175348447980

Bu hesap tarzı (0^oC ≤  t_c ≤ 373^oC için geçerlidir. Aynı şekilde “ters denklem” tabir edeceğimiz işlemle de doyma basıncından hareketle doyma sıcaklığını hesaplayabiliriz.

t_Cdp= (0.5 x (N₁₀+ D –((N₁₀+ D)²-4(N₉+N₁₀x D))^0.5))-273.15

Bu formülde :

D= 2G/(-F-(F²-4E x G)^0.5)

E= β²+ N₃x β + N₆

F= (N₁x β²) + (N₄x β) + N₇

G= (N₂x β²) + (N₅x β) + N₈

“β” değeri ise aşağıdaki formülle hesaplanır:

β= ( p_ws/1000)^0.25………………….. (p_ws= kPa)       

2.4.4. Mutlak Nem Miktarının (Nem Oranının) belirlenmesi

Havadaki mutlak nem miktarı (nem oranı) “W” bir kilogram kuru hava içinde bulunan nem miktarının orantı olarak belirtilmesidir. Bu orantı (kg_wv/kg_da) olarak ifade edilir.

Bağıl nem ise belirli bir kuru termometre sıcaklığındaki mutlak nem miktarının aynı sıcaklıkta doyma noktasındaki mutlak nem miktarına oranıdır. Bu tabir “%” olarak ifade edilir.

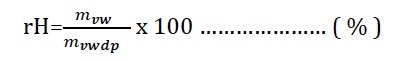
Mutlak nem miktarının hesaplanmasını da aşağıdaki tar-zda ve Dalton Kanunu’ndan yararlanarak yapabiliriz.

p.V = m . R . T

Bu formülü “m” değerini hesaplamak üzere tekrar düzenlersek:

m = (p . V)/( R . T ) 

 bulunur. Aynı formülü su buharı ve kuru hava için düzenlediğimizde aşağıdaki denklemlere ulaşırız.

m_vw= (p_vws. V_vws)/( R_wv. T )  …….. su buharı için

m_da= (p_da. V_da)/( R_da. T )  ………kuru hava için

 m_vw/m_da=((p_wvs. V_wvs)/( R_wv. T ))/( (p_da. V_da)/( R_da. T )) 

 Dalton Kanunu’na göre su buharı ile kuru hava aynı hacmı paylaşmaktadır. Bu nedenle:

V_vws= V_da

 Keza aynı şekilde her iki gazın ortam sıcaklığı da birbirlerine eşittir. Bu nedenle eşit değerler birbirini götüreceği için denklem aşağıdaki şekle dönüşür.

m_vws/m_da=(p_vws/ R_wv )/(p_da/ R_da) 

 R_wv= 461.52 kJ/kg

R_da= 287.06 kJ/kg

 Bu değerleri yerine koyduğumuzda

m_vw/m_da=0.621945 . p_vw/p_da       bulunur.

p_da= P – P_{vws                                      olduğundan aşağıdaki sonuç formül karşımıza çıkar.}

m_vw/m_da=0.621945 . p_wvs/(p– p_wvs)

 2.4.3 No’lu bahiste doyma nokta sıcaklığındaki buhar basıncını ve o noktadan hareketle doyma noktası sıcaklığının hesaplanacağını incelemiştik. Şimdi de o sıcaklığa tekabül eden mutlak nem miktarını buhar basıncına bağlı olarak nasıl hesaplanacağını görmüş olduk.

 2.4.5. Havanın Özgül yoğunluk ve özgül hacminin belirlenmesi

 P.v_{da_0C}= m . R . T

 Bu denklemde :

P          = Atmosferik basınç, 101325 Pa

v_{da_0C}  = Özgül hacım. 0^oC kuru hava için (m³/kg_da)

m         =Havanın moleküler ağırlığı. 28.964 kg/kmol

R          = Üniversal gaz sabiti . 8314.41 J/(kmol.K)

T          = havanın sıcaklığı ( ^oK)

Değerleri denklemde yerlerine koyup, “v_{da_0C}”için çözdüğümüzde:

v_{da_0C}=((8314.41)x(273.15 + 0))/(28.964×101325)

 v_{da_0C}= 0.773851 …………………………….  (m³/kg_da-0C)

 Havanın özgül yoğunluğu: δ_{da_0C}= 1/ v_{da_0C} olduğuna göre:

δ_{da_0C}= 1/ 0.773851=1.2922 … (kg_da-0C/m³) bulunur.

Bu formülü genelleştirdiğimiz zaman, derğişik sıcaklıklardaki kuru havanın özgül hacmini aşağıdaki formülle hesaplayabiliriz.

v_da= 0.0028333 (273.15 + t_da)

 Kuru havanın hesapla bulunan özgül ağırlığına aynı sıcaklıktaki doyma noktasındaki havanın içinde bulunan su buharının ağırlığının ilavesi ile doyma noktasındaki havanın özgül hacmi ve özgül ağırlığı bulunur.

δ_a= δ_da+ W_wv