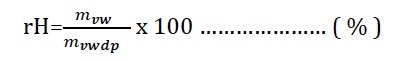Ay: Aralık 2018

4. PSİKROMETRİK DİYAGRAMLAR

4.1. GENEL

İlki 1904 yılında Willis Carrier tarafından yapılan ve günümüze kadar, araştırmalar neticesi devamlı gelişme gösteren Psikrometrik Diyagramlar nemli havanın termodinamik özelliklerinin yansıtıldığı tablolardır. Ancak bu tablolarda entropi ve buhar basıncı gösterilmez. Ancak buhar basıncının mutlak nem oranı ve doyma noktası ile olan matematiksel ilişkisi nedeniyle biz psikrometrik diyagramlarımıza buhar basıncını mutlak nem oranı ordinatına paralel bir çizgi olarak ekledik.

-40^oC ile +120^oC aralığı ve 101.325 kPa atmosferik basınç için tek bir diyagram hazırlamak mümkündür.

Ancak bu diyagramda normal ve düşük sıcaklıklardaki değerleri, örneğin A4 veya A3 ölçülerindeki bir psikrometrik diyagramda okumak çok zor olacağından ASHRAE bunu üçe bölerek kolaylaştırmıştır. Birinci tablo 0^oC ila 50^oc arasındaki sıcaklıklara, konfor klimasının genelde uygulamasının yapıldığı şartlara hitap etmektedir. Bunu tamamlayıcı mahiyette iki psikrometrik diyagram daha bulunmaktadır. Bu diyagramlardan biri -40^cC ila +10^oC aralığına hitap eden “düşük sıcaklık” psikrometrik diyagramıdır. Diğeri ise “yüksek sıcaklık”diyagramıdır. Bu diyagram +10^oC ile +120^oC aralığını kapsamaktadır. Yüksek sıcaklık psikrometrik diyagramı özellikle yüksek sıcaklıklarda ısı geri kazanımı prosesleri ile absorbsiyonlu nem alma proseslerinin etüdü açısından çok faydalı olmaktadır. Bu diyagramların tamamı 101.325 kPa basınca tekabül eden deniz seviyesi içindir. Birinci bölümde bahsedilen konulardaki formüllerle değişik irtifalar için de psikrometrik diyagramların çizimi mümkündür.

Bu durum karşımıza psikrometrik diyagramlarda üçüncü bir ekseni ortaya çıkarmaktadır. “Z” ekseni olarak adlandırabileceğimiz bu eksen deniz seviyesinden olan yüksekliktir. Aşağıdaki resimde 0 ve 1500m irtifalarda birçok değerin değişimi izlenmektedir.

Örneğin kuru havanın özgül hacmi artmakta, kuru termometre sıcaklıklarının doyma noktalarındaki mutlak nem oranları da keza artmaktadır. Bunların yanı sıra özgül entalpilerde de farklılıklar meydana gelmektedir. Buradan da klima proseslerinin en doğru ve/veya irtifa açısından en yakın psikrometrik diyagramlara işlenmesi, örneğin ısıtma-soğutma yükleri, nemlendirme miktarı, nem alma işlemi için gereken soğutma yüklerinin bu diyagramlarda belirlenmesi şarttır. Aksi halde diyagram üzerinden yapılacak hesaplamalar belirli hata oranlarına sahip olacaktır.

4.2. DENİZ SEVİYESİ PSİKROMETRİK DİYAGRAMLARI

4.2.1. Normal Sıcaklık Psikrometrik Diyagramı

-10^OC ila +50^oC arasındaki sıcaklıklara hitap eden, İMEKSAN A.Ş.’nin kullandığı psikrometrik diyagramı burada sunuyoruz. Çünkü bu sayede dış hava sıcaklığı 0^oC’ın altında olan yerlerde de ısıtma yüklerini diyagram üzerinde belirlemek mümkün olmaktadır. Ayrıyeten bu diyagramda buhar basınçları da kırmızı bir koordinat  ile gösterilmektedir.

4.2.2. Düşük Sıcaklık Psikrometrik Diyagramı

  

4.2.3. Yüksek Sıcaklık Psikrometrik Diyagramı

4.3. DENİZ SEVİYESİNDEN YÜKSEK MAHALLER İÇİN PSİKROMETRİK DİYAGRAMLAR

4.3.1. Genel

ASHRAE’in  geliştirdiği psikrometrik diyagramlar arasında üç tane de yüksek irtifalar için psikrometrik diyagramlar bulunmaktadır. Bu diyagramlar 750 metre, 1500 metre ve 2250 metre içindir. Ancak ülkemiz dikkate alındığında bu diyagramların 500 metre, 1000 metre, 1500 metre ve 2000 metre irtifalar için yapılmasında büyük faydalar vardır.

İrtifaya bağlı değişkenler içinde başta barometrik basınç gelmektedir. Barometrik basınç deniz seviyesinden olan yükseklik arttıkça, buna bağlı olarak düşüş göstermektedir. Bu değişikilk 2.4.1’deki tabloda gösterilmiştir. Aynı tabloyu burada bir daha veriyoruz.

Yukarıdaki tablodaki atmosferik basınç değerleri , aşağıdaki formülle hesaplanmıştır.

P_bar=101,325 (1- 2,25577 x 10^-5 x Z)^5,2559

                                Z=Deniz seviyesinden irtifa (m)

Buhar basıncı da 3.9’da aşağıdaki gibi ifade edilmişti.

P_wv=1.6077W(101.325(1 – 2.25577 x 10^-5x Z )^5.2559-P_wv)

Bu formüllerden hareketle psikrometrik diyagramı oluşturabilmemiz için gerekli doneleri aşağıdaki gibi formülize edebiliriz:

Mutlak nem oranı: ( bkz.konu 3.8 )

W=0.622P_wv/(P_bar-P_wv)…………………………………………. (g/kg)

 Özgül hacım:

γ= V/m_a=(R_a.T)/(P_bar-P_wv) =(R_a.T)/(1+ w/622).(m³/kg)

 Özgül Entalpi:

h= h_da+ W.h_wv=1,005t + W(2,501 + 0,001805 x t )..(kJ/kg)

 Bu formüller esas alınarak hesaplanmış olan 0, 500, 1000, 1500 ve 2000 metre irtifaların psikrometrik tabloları  üçüncü bölüm, konu-8 “Tablolar”da verilmektedir.  Ayrıca ASHRAE psikrometrik diyagramları esas alınarak geliştirilmiş 750m, 1500m ve 2250m irtifalara ait psikrometrik diyagramlar da aşağıda gösterilmektedir.

4. PSİKROMETRİK ÖZELLİKLER VE TERİMLER

3.1. Giriş

Üç temel piziki öge belirlendiği ve sabit olduğu sürece kuru hava ile su buharının karışımı sabittir ve değişemez. Bu ögeler şunlardır:

a) Barometrik basınç (veya irtifa)…………………………..( P_atm)
b) Kuru termometre sıcaklığı………………………………….( t_db)
c) Aşağıdaki üç değişkenden herhangi biri

• Yaş termometre sıcaklığı veya…………………( t_wb )
• Bağıl nem veya………………………………………(rH )
• Çiy noktası………………………………………………( t_dp)

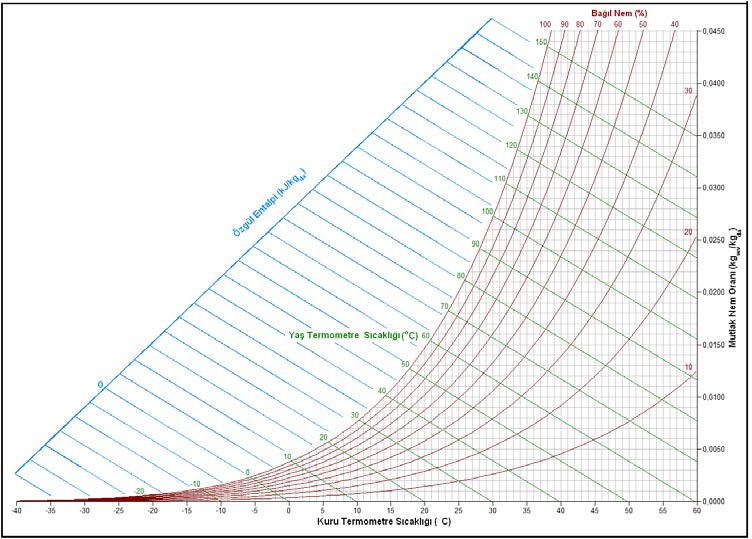
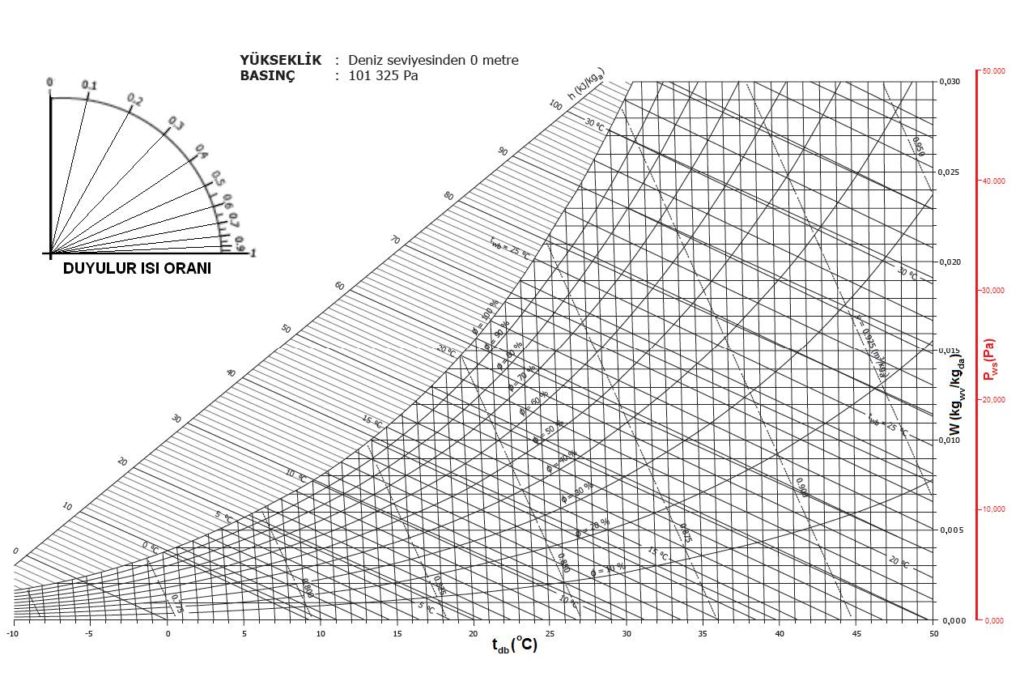
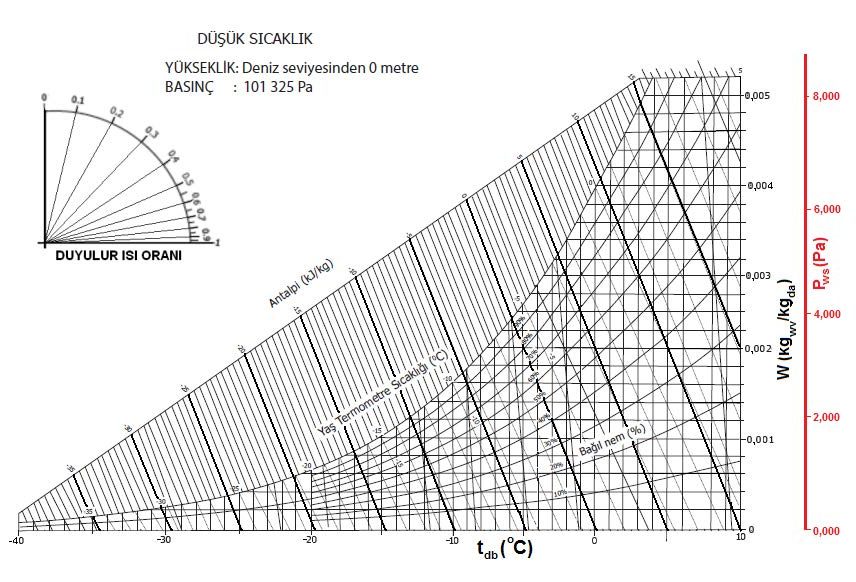
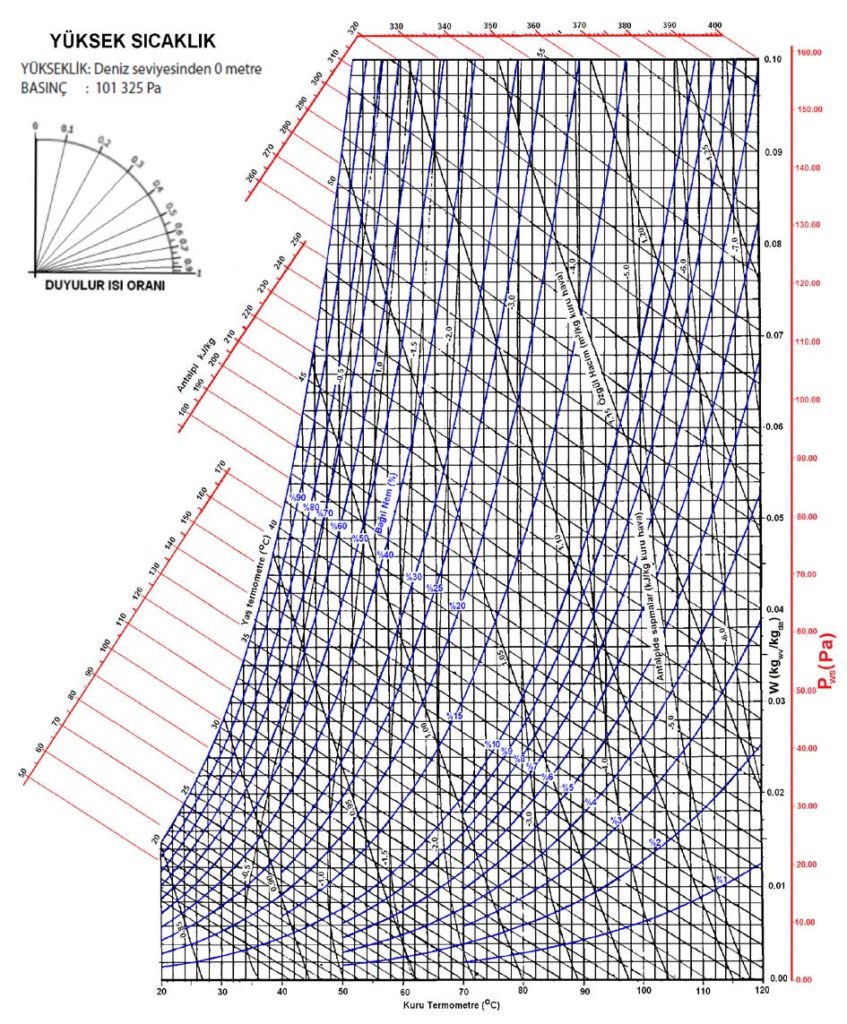
“c” şıkkındaki üç unsur birbirine bağlı olduğu için “a”,”b” deki ögelerle “c” deki ögelerden birinin belli ve sabit olması  kuru hava ile su buharı karışımının durumunu da belirler ve sabitler. Bu husus aynı zamanda “c” şıkkındaki diğer iki değişkeni de belirler ve sabitler. Bu özellikler aşağıdaki psikrometrik diyagramda gösterilmiştir.

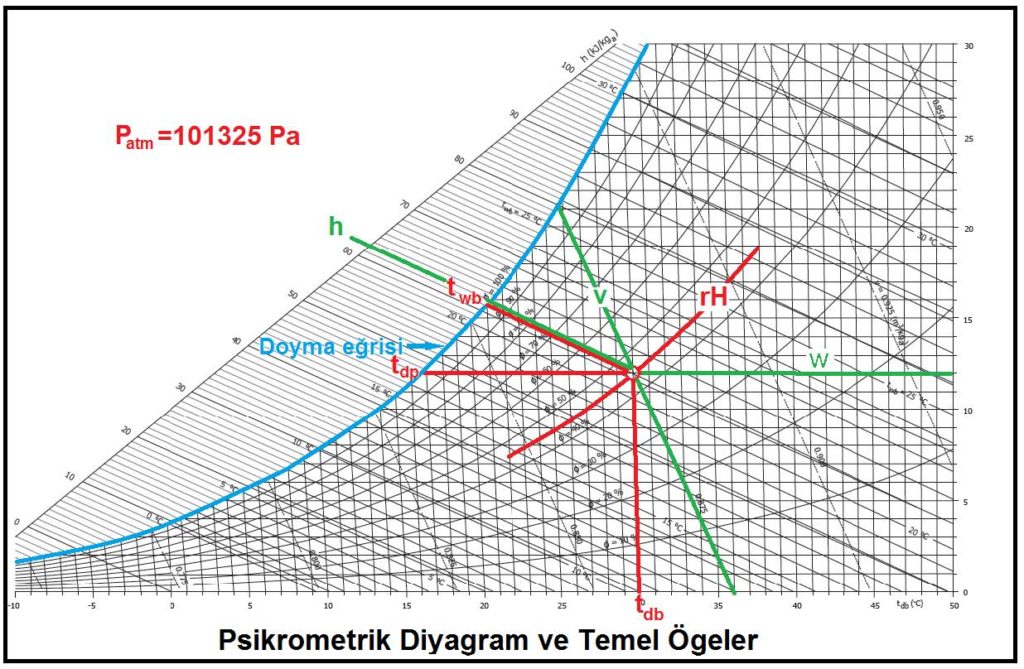
Bu diyagramda temel psikrometrik konumu belirleyen ögeler kırmızı renkte gösterilmiştir. Bu ögelerin yardımıyla diğer önemli üç doneyi de psikrometrik diyagramdan okumak mümkündür. Bu doneler şunlardır:

• Entalpi ……………………………………………………( h)
• Mutlak nem…………………………………………….(w )
• Özgül hacım……………………………………………( v )

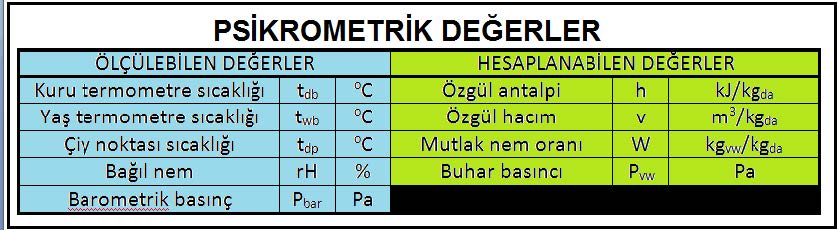
Bu sayede dokuz temel nokta belirlenmiş olmaktadır. Bu noktalardan beşine ölçülebilen değerler, diğer dördüne de hesaplanabilen değerler diyebiliriz. Bu husus aşağıdaki tabloda özet olarak gösterilmektedir.

 3.2. Kuru Termometre Sıcaklığı

Kuru termometre sıcaklığı herhangi bir alkollü ve civalı termometre ile veya aynı değerlere kalibre edilmiş hissedici+transduser ile ölçülen mahal veya çevre sıcaklığıdır. Bu sıcaklık “t_db” sembolü ile gösterilir. Birimi ise “^oC”veya “K”dir. Daha önceki bahislerde anlatıldığı gibi “^oC” Celsiyus skalası olup bu skalada 0^oC deniz seviyesinde suyun donma sıcaklığına, 100^oC ta deniz seviyesinde suyun kaynama noktasına tekabül etmektedir. “K” ile gösteriklen Kelvin ölçeği ise mutlak sıfırı esas almıştır, bu sıcaklık Selsiyus skalasında -273.15^oC’a eşittir.

Kuru termometre sıcaklığı psikrometrik diyagramda “^oC” olarak diyagramın altında , absisinde yer alır ve düşey hatlar ile gösterilir.

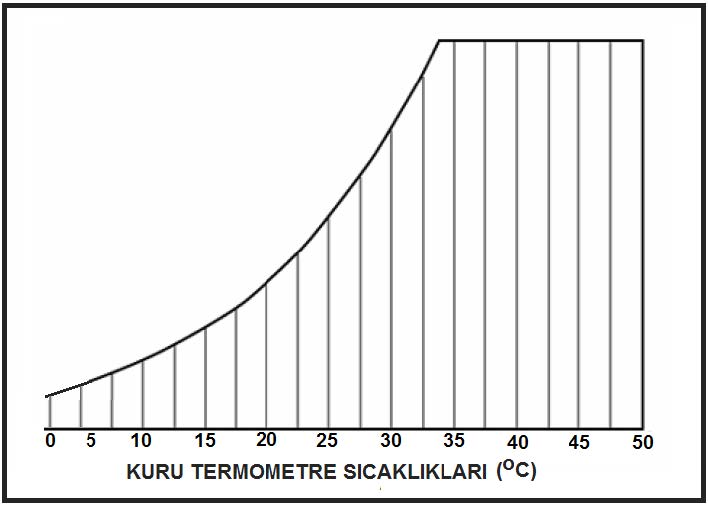
Kuru termometre sıcaklığı gösteren absiste 0^oC kuru hava sıcaklığı aynı zamanda entalpik değerlerin başlangıç, yani referans noktası olarak kabul edilir ve bu noktadan itibaren kuru havanın entalpik değerleri hesaplanır. Bu hesaplamayı aşağıdaki formüller ile gösterebiliriz.

Q=M. C_p-da(t_2db-t₀)

Bu denklemde “t₀” havanın entalpik hesaplamada referans noktası olan  0^oC sıcaklığı, “t₂”iseentalpisinin ölçülmesi istenen kuru havanın sıcaklığını göstermektedir. “C_p-da” değeri ise havanın özgül ısısıdır; birimi “kJ/kg”dır.

C_p-dakuru havanın özgül ısısıdır. Özgül ısı bir kilogram ağırlığındaki bir nesnenin ısısını 1^oC arttırmak için gerekli olan ısıdır. Bu değer 15^oC’taki bir kilogram suyun ısısını bir derece arttırmak için gerekli olan ısıya orantılı olarak belirlenir. Bu değer kCal/h birimleriyle su için 1.00 kCal/kg, kuru hava için 0.24 kCal/kg’dır. Uluslararası kullanımda olan “SI” birimleriyle ifade edildiğinde kuru havanın özgül ısısı 1.00483 kJ/kg’dır. Su buharının özgül ısısı da 1.83’dür. Havanın özgül ısısı kuru termometre sıcaklığına bağlı olarak çok az değişiklik göstermektedir. 1.00483 kJ/kg değeri esas alındığında -10^oC ile +50^oC arasında yapılacak hesaplarda hata payı %0.2’den küçük olmaktadır. Aşağıdaki tabloda “C_p” değerindeki değişmeler gösterilmektedir.

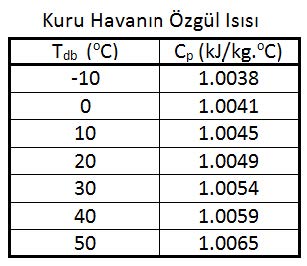
Aynı şekilde su buharının özgül ısısında da aynı sıcaklık aralığında çok küçük, kabili ihmal farklılıklar olmaktadır.

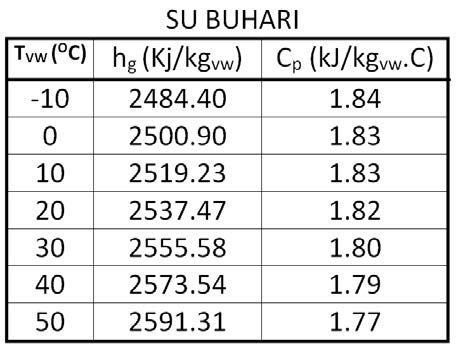
Dolayısıyla su buharının özgül ısısını 1.82 kJ/kg.C olarak kabul edebiliriz.

Bir önceki sayfadaki formülü birim kitle, 1 kg kuru hava için yaptığımızda kuru havanın “t₂” sıcaklığındaki antalpisini hesaplamış oluruz.

h_2da=C_p-da(t_2db-t₀)

Doymuş havanın entalpisini de kuru havanın entalpisi ile doyma noktasındaki mutlak nem oranının buharın özgül ısının çarpımının toplamı olarak bulabiliriz.

h_2sa=C_p-da(t_2db-t₀) + C_p-vw.W(t_2db-t_o)

 h_2sa=t_2-da(C_p-da+ C_p-vw.W)  …………………………(kJ/kg)

3.3. Yaş Termometre Sıcaklığı ve Adyabatik Doyma

Yaş termometre ile ilgili birçok tarif vardır. Bunlardan biri yaş termometre sıcaklığını “buharlaşma sıcaklığı” olarak, diğer bir tarif  te  “%100 doyma noktasına gelinmesi ile neticelenen evaporatif soğutma neticesi elde edilebilen en düşük sıcaklık” olarak tarif eder.  Termodinamik yaş termometre sıcaklığına aynı zamanda adyabatik doyma sıcaklığı da denmektedir.

Yaş termometre sıcaklığı “termodinamik yaş termometre sıcaklığı” ve “psikrometrik yaş termometre sıcaklığı”olarak ta tarif edilmektedir. Termodinamik yaş termometre sıcaklığı suyun buharlaşması ile havanın adyabatik olarak soğuması sonucu elde edilebilen en düşük sıcaklıktır. Sıvı haldeki su doymamış hava ile temas ettiğinde kısmi buhar basıncı farkı nedeniyle buharlaşır (bu konu ileriki bahislerde detaylı bir biçimde incelenecektir) . Bu buharlaşma işlemi adyabatik bir prosestir. Çünkü dışarısıyla hiçbir ısı alış-verişi yoktur. Buharlaşma için gerekli ısı havadan temin edilir ve bunun neticesi olarak hava soğur ama içindeki mutlak nem oranı artar. Neticede hava-buhar karışımının antalpik değeri sabit kalır.

Termodinamik yaş termometre sıcaklığı adyabatik doyurucudaki kitle ve enerji balansları dikkate alınarak ölçülür. Bu nedenle termodinamik yaş termometre sıcaklığına adyabatik doyma sıcaklığıda denir.  Adyabatik doyurucu olarak adlandırılan enstruman aslında teoretik bir enstruman olup mutlak izolasyona sahip olması ve çok uzun (sonsuza yakın) bir boyda olması gerekir.

Mollier Diyagramı’nda ve 1963’den itibaren ASHRAE’in Psikrometrik Diyagramları’nda izometrik çizgiler halinde gösterilen yaş termometre sıcaklığı çizgileri bu ölçme tekniği ile belirlenen termodinamik veriler esas alınarak tanzim edilmiştir. Aşağıdaki resimde adyabatik doyurucunun şematik bir çizimi yer almaktadır.

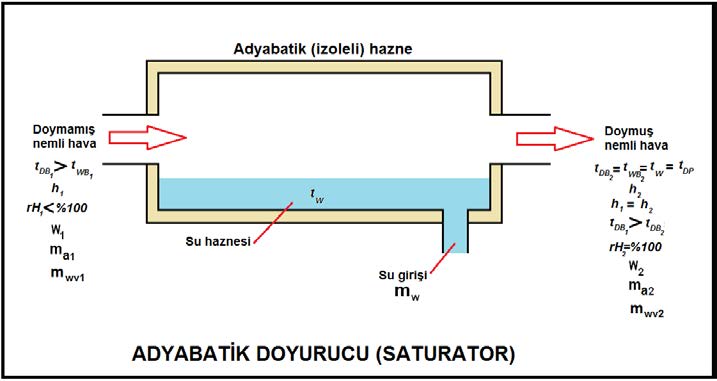
Kuru hava ve su buharı karışımı ile belirlenen psikrometrik yaş termometre sıcaklığı klasik bir termometrenin, örneğin cıva veya alkollü cam termometrenin hissedici ucunun yumuşak ve temiz bir pamuk sarılması, pamuğun iyice ıslatıldıktan sonra 3 ila 5 m/s hava hızına tabi tutulması ile ölçülür. Islatılmış uç üzerinden geçen hava akımı suyun buharlaşmasına ve termometrede gösterilen sıcaklığın düşmesine neden olacaktır. Bir müddet sonra ölçme kararlı rejime giriiecek, termometrede görünen değer sabitlenecektir. Bu değer psikrometrik yaş termometre sıcaklığıdır. Bu ölçme işlemi esnasında termometrenin ve özellikle ucunun güneş radyasyonuna maruz bırakılmaması gerekir. Ölçme ucunu kaplayan pamuk devamlı ıslak tutulmalıdır. Bunun için pamuğun fitil tarzında uzatılması ve bir su haznesine batırılmış olması gerekir (bkz. Bölüm-1 HYDRODEIK). Benzer bir yaş termometre psikrometresi aşağıdaki resimde gösterilmektedir.

Kuru termometre ile yaş termometre sıcaklıkları rarsındaki farkın (t_db-t_wb) 10^oC’tan büyük olması  fitilin hareket halindeki hava ile teması esnasında ısınmasına ve bu ısının hazneye iletilerek suyun bir miktar ısınmasına neden olur. Böyle durumlarda ölçülen yaş termometre sıcaklıkları olması gereken değerlerden biraz yüksek çıkabilir.

Buradaki işlem adyabatik doyurucudaki işlemin birebir aynı değildir. Ancak psikrometrenin uygun bir yere yerleştirilmesi koşuluyla iki ölçüm arasındaki sapmalar ihmal edilebilecek minimum seviyelerde tutulabilir.

Adyabatik Doyurucu’da yapılan işlemi termodinamiğin iki temel kanununun ışığı altında inceleyebiliriz. Adyabatik doyurucuya giren kuru havanın debisi “m_a1”, çıkan havanın debisi de “m_a2” gösterilmektedir. Buharlaşan su miktarı da “m_w” dir. “w₁”ve “w₂” giriş ve çıkıştaki havanın içindeki mutlak nem oranını göstermektedir. Kitlenin korunumu kanununa göre denklemimizi kurarsak:

m_a1=m_a2=m_a……………………………..(kuru havanın debisi)

m_wv1+m_w=m_wv2…………………………..(havadaki buharın debisi)

Bu denklemi su buharı için aşağıdaki gibi de yazabiliriz.

m_a.w₁+ m_w= m_a.w₂

Böylece:

m_w=m_a(w₂-w₁)…………………………….. (buharlaşan suyun debisi)

Benzer denklemleri de enerjinin korunumu kanununa göre yazabiliriz.

∑m₁.h₁=∑m₂.h₂

Bu denklemde “m₁” girişteki doymamış nemli havanın kütlesini, “m₂”ise çıkıştaki doymuş nemli havanın kütlesini, “h₁” ve “h₂”ise aynı havaların giriş ve çıkıştaki antalpilerini, “h_wv1” ve “h_wv2”  su buharının giriş-çıkıştaki entalpilerini, “h_w”ise suyun entalpisini göstermektedir. göstermektedir. Buradaki eşitliğin nedeni prosesin adyabatik olmasından, dışarı ile herhangi bir enerji transferi olmamasından kaynaklanmaktadır.

Aynı denklemi şöyle de yazabiliriz:

m_a.h₁+ m_w.h_wv2 = m_a.h₂

m_a.h₁+ m_a(w₂-w₁).h_wv2 = m_a.h₂

Bu denklemi “m_a” kemiyetine böldüğümüzde aşağıdaki denklemi buluruz.

h₁+ (w₂-w₁).h_wv2 = h₂

(C_p.t_db1+ w₁.h_wv1)+(w₂-w₁)h_w2=(C_p.t_db2+w₂.h_vw2)

w₁=(C_p(t_dp1-t_dp2)+w₂.h_vw2)/(h_wv1-h_w2)……bulunur.

Daha önceki hesaplarımızda “m_wv/m_da”mutlak nem oranını aşağıdaki gibi hesaplamıştık:

m_wv/m_da=0.621945. P_wvs/(P- P_wvs) 

m_wv2/m_da=w₂ olduğuna göre yukarıdaki denklemde “w₁”değerini yerine koyduğumuzda “w₁” değerini de hesap yoluyla bulmuş oluruz.

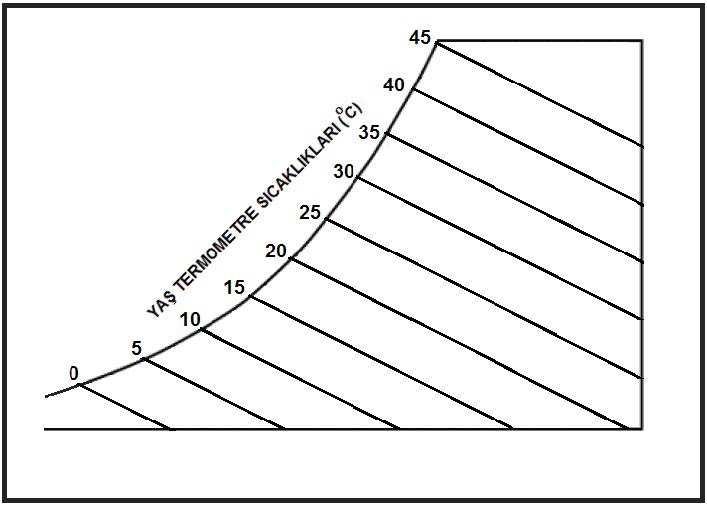
Yaş termometre sıcaklıkları ASHRAE’in psikrometrik diyagramlarında ve Mollier’in i-x diyagramında birbirine paralel eğimli düz çizgiler olarak gösterilir. Bu çizgiler sabit antalpi çizgilerine de paraleldir.

• Çiy Noktası ve Çiy Noktası Sıcaklığı

Çiy noktası sıcaklığını satıh kondansasyonunun oluşmaya başladığı sıcaklık olarak tarif edebiliriz. Benzeri bir tarif ile, çiy noktasını havanın doyma noktasına eriştiği, daha fazla buhar kabul edemeyeceği sıcaklık olarak ta tanımlayabiliriz. Eğer buhar ilave edilmeye devam edilirse sis, satıh yoğuşması veya bulutlar oluşmaya başlar.

Çiy noktasının daha ilmi bir tarifi de yoğuşabilir herhangi bir buharın sabit basınçta yoğuşma başlamadan önce erişebileceği sıcaklıktır. Dolayısıyla doyma sıcaklığı ile çiy noktası sıcaklığı birbirine eşit anlamdaki tabirlerdir.

Çiy noktası sıcaklığını  basit bir deneyle kendimiz de yapabiliriz.

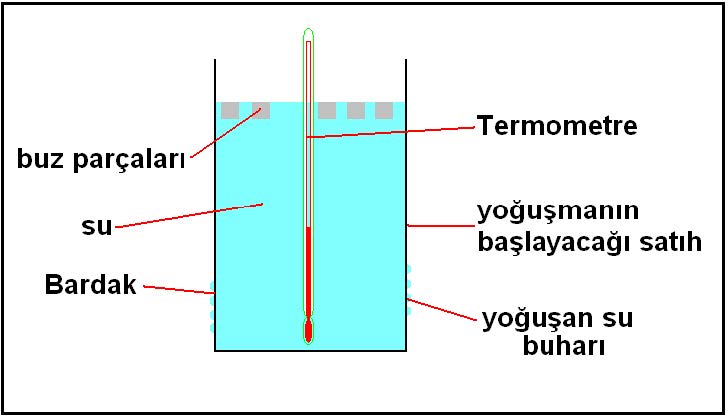
Bir bardağın içine oda sıcaklığında su kouyn. İçine de bir termometre daldırın. Bardağın içine azar azar buz ilave edip termometredeki düşmeyi izleyin. Bir süre sonra bardağın dış sathında su zerrecikleri belirmeye başlayacaktır. Bu zerrecikler yoğuşan havadaki su buharıdır. Yoğuşmanın başladığı andaki sıcaklık değeri de odanızın çiy noktasıdır.

Herhangi bir kuru termometre ve yaş termometre sıcaklıkları ile belirlenen ortam soğutulmaya başlandığında önce duyulur soğutma işlemi gerçekleşir (Bkz. Bölüm-5, konu 5.4.1 ve 5.4.2). Belirli bir sıcaklığa gelindikten sonra mahal havasının içindeki buhar da yoğuşmaya başlar ve bu noktadan itibaren duyulur ve gizli soğutma işlemleri beraber devam eder.

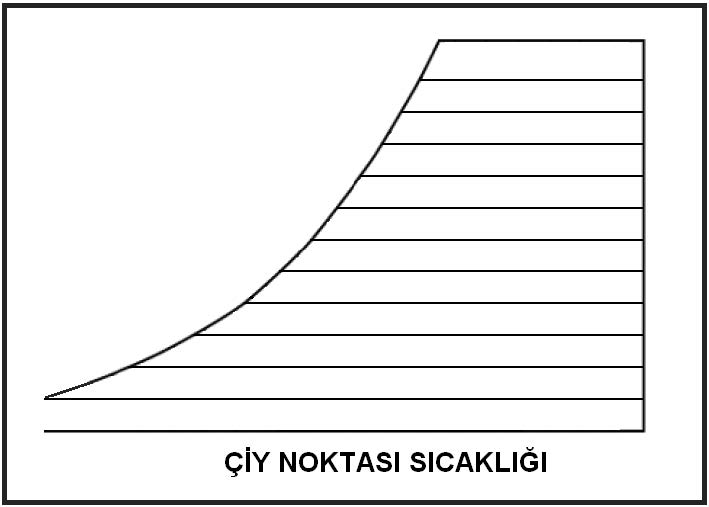
Çiy noktası mahal şartlarından kuru termometreyi belirleyen absise paralel bir çizginin çizilmesi ile bulunur. Bu çizginin doyma eğrisini kestiği nokta o ortamın çiy noktası sıcaklığıdır. Bu sıcaklık doyma noktası sıcaklığına eşittir.

Aynı zamanda bu noktanın kuru termometre ve yaş termometre sıcaklıkları da eşittir.

3.5. Bağıl Nem

-40^oC ila +65^oC arasındaki sıcaklıklarda yapılan deneyler su buharının ideal gaz karakteristiklerine sahip olduğunu göstermiştir. Bu görüş açısından hareketle bağıl nemi ortam şartlarında mevcut mutlak nem oranının aynı kuru termometre sıcaklığındaki mutlak nem oranına oranı olarak ifade edebiliriz. Bağıl nem için kulanılan simge “rH” olup “%” olarak ifade edilmektedir ve birimsiz bir kemiyettir.

rH (%)= (W_t1/Wdp._t1).100

Aynı orantıyı (kısmi) buhar basınçlarının oranı olarak ta ifade edebiliriz.

rH (%)=(P_wv-t1/P_wv-dp-t1).100

 

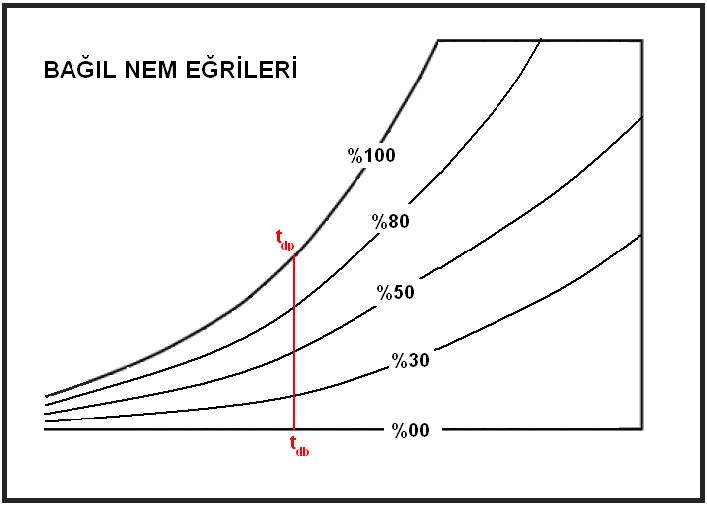
Yukarıdaki psikrometrik diyagramdan da anlaşılacağı gibi “t_db”kuru termometre şartlarındaki bir ortamda olabilecek mutlak nem oranı (miktarı) sıfır ile “t_dp”nin tekabül ettiği nem oranı arasında değişiklik gösterebilmektedir. Belirtilen sıcaklıktaki mutlak nem miktarının yüzde ellisi “rh%50”i,yüzde sekseni “Rh%80”i, yüzde otuzu da “Rh%30”a tekabül etmektedir.

Burada bilinmesi gereken bir olay vardır. Gün batımına yakınlaştıkça bağıl nem oranı artar. Bu işlem havanın duyulur soğuma işlemine tabi olmasından kaynaklanmaktadır. Havadaki mutlak nem değişmediğinden soğumaya bağlı olarak bağıl nem oranı artış gösterir. Bu soğuma devam eder ve çiy noktası sıcaklığının altına düşerse, örneğin arabalarımızın camlarında gördüğümüz su zerreciklerini görürüz. Eğer sıcaklık 0^oC’ın altındaysa çiy yerine kırağı ile karşılaşırız.

3.6. Barometrik Basınç 

Basınç bir birim alana onun üzerindeki kütlenin ağırlığı ile tatbik olunan kuvvete verilen isimdir. Aynı şekilde barometrik basıncı da herhangi bir belirgin konumda birim alana üzerindeki havanın ağırlığı ile tatbik olunan kuvvet olarak tarif edebiliriz. Psikrometrik proseslerde barometrik basınç ile atmosferik basınç eş anlamlı olarak kullanılmaktadır.

Barometrik basınç deniz seviyesinden olan irtifa ile değişmektedir. Atmosferin belirli bir kalınlığı olduğu kabulü ile barometrik basıncın deniz seviyesinden derinlere inildiğinde artacağı, yükseklere çıkıldığında da azalacağı kolaylıkla anlaşılabilir. Barometrik basınç “barometre” olarak adlandırdğımız, genelde cıva içeren bir ölçme aleti ile ölçülür. ASHRAE STP tarifine göre deniz seviyesindeki basınç 29.92 inHg, 760mmHg veya 101.325 kPa (kilopaskal)’dır. Günümüzde cıvalı barometrelere ilaveten körüklü “aneroid” tipi veya spiralli mekanik barometreler ve elektronik dijital barometreler de kullanılmaktadır.

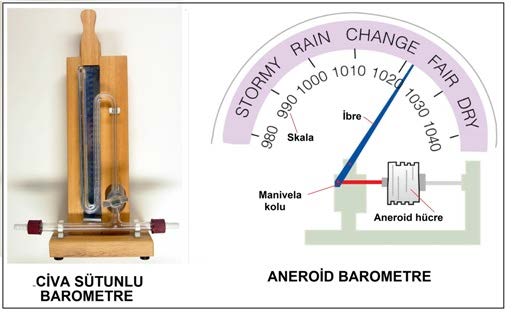
Eğerbelirli bir noktadaki barometrik basınç bilinmiyorsa, basıncı ICAO (Uluslar arası Sivil Havacılık Kurumu)’nun 1925 yılında yayınlamış olduğu formüle göre hesaplamak mümkündür. Konu 2.4.1’de vermiş olduğumuz formülü tekrar veriyoruz.

P_bar= 101.325 (1-2.25577 x 10^-5x Z)^5.2559……….(kPa)

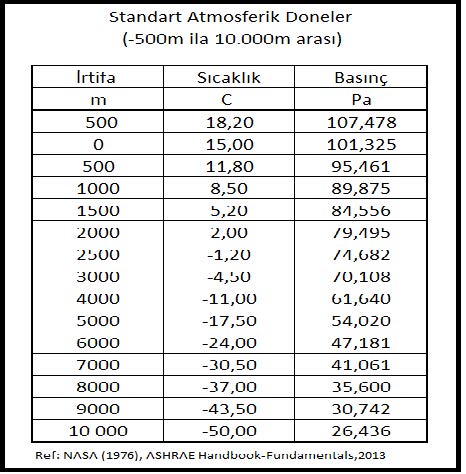
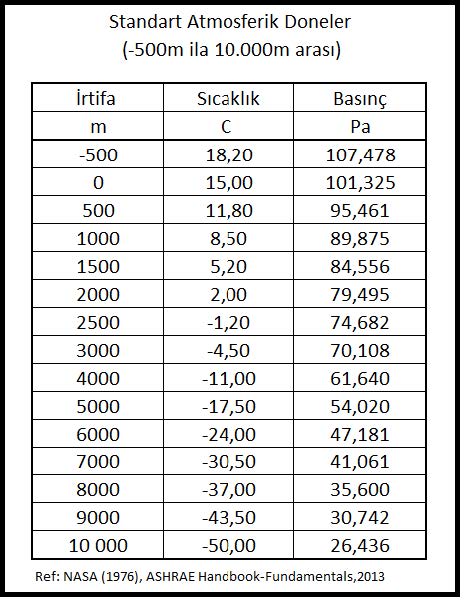
 Buformülde “Z” metre cinsinden irtifayı göstermektedir. İrtifaya bağlı olarak basınç ve sıcaklık değerlerinin değişimi Konu-2.4.1’deki “Standart Atmosferik Doneler” tablosunda -500m ila 10 000m arasındaki irtifalar için gösterilmektedir.

Barometrik basınç kuru havanın basıncıyla su buharının basıncının toplamından oluşmaktadır. Herhangi bir belirgin konumdaki barometrik basıncı  birim alan üzerindeki havanın ağırlığı ile tatbik olunan kuvvet olarak tarif etmiştik. Ancak havanın özgül hacminin artması ki bu genellikle sıcaklık artışına bağlı olarak meydana gelir, kuru hava basıncının azalmasına neden olur. Barometrik basınç sabit olduğuna göre eksilen kısmi basıncı su buharı tamamlayacaktır.

P_bar= P_da + P_wv

Diğer bir yaklaşımla, kuru havanın basıncındaki değişikler barometrik basıncı oluşturan ikinci ögeyi etkilediğini, bu nedenle kuru hava kısmi basıncının azalması su buharı kısmi basıncının artmasına neden oluşturduğunu söyleyebiliriz. Aynı şekilde kısmi kuru hava basıncındaki artışlarda kısmi buhar basıncında eksilmelere neden oluşacağı, bu işlemin de havadaki su buharının yoğuşması suretiyle gerçekleşeceği psikrometrinin temel oluşumlarından biridir.

Psikrometrik prosesler esnasında barometrik basıncın sabit olduğu kabul edilir. Tüm klima hesaplarında bu husus aynen kabul edilmekte, meteorolojik olaylar neticesi barometrik basınçta meydana gelebilecek küçük değişmeler kabili ihmal kabul edilmektedir.

 Barometrik basınç psikrometrik özelliklerin belirlenmesi ve sabitlenmesi için gerekli üç temel ögeden biridir. Diğer ögelerin başında kuru termometre sıcaklığı ile yaş termometre sıcaklığı gelir. Yaş termometre sıcaklığı yerine mutlak nem oranını veya bağıl nemi de kullanabilirsiniz. Barometrik basınç psikrometrik diyagramlarda bir koordinat olarak yer almaz. Ancak her barometrik basınç için ayrı bir psikrometrik diyagramın çizilmesi gerekir. Bu nedenledir ki ASHRAE deniz seviyesi (101.325 kPa) için ayrı, 750 metre (92.834 kPa) için ayrı, 1500 metre (84.556 kPa) için ayrı ve 2250 metre (77.058 kPa) için ayrı psikrometrik diyagramlar tanzim etmiştir. Bu diyagramlar 4. Bölüm’de detaylı olarak incelenecektir.

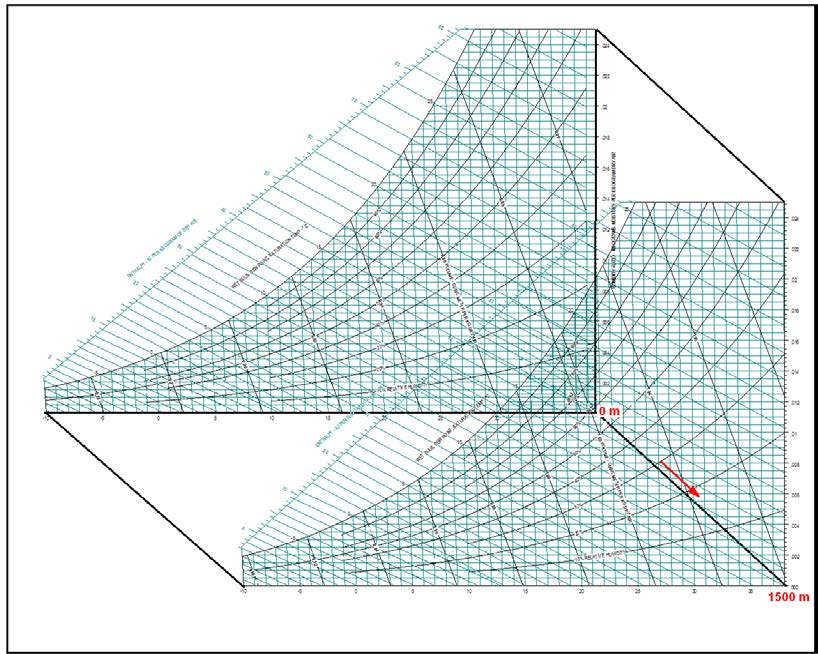
Barometrik basıncın irtifa nedeniyle azalması da hava içinde bulunabilecek mutlak nem oranını etkilemektedir. Basıncın düşmesi neticesi kısmı buhar basıncı ve buna bağlı olarak mutlak nem oranı artmaktadır. Bu değişikliği aşağıdaki diyagramda görebiliriz.

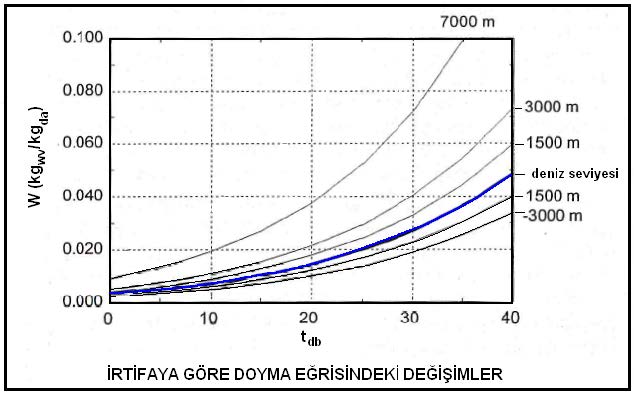
Ref.:Understanding Psychrometrics, Donald P. Gatley, ASHRAE

3.7. Özgül Hacim

Özgül hacim psikrometride kuru havanın birim kitlesinin işgal ettiği hacim olarak tarif edilir. Birimi beher kilogram başına düşen metreküp olup “m³/kg_da” olarak gösterilir sembolü de “v” harfidir. Dalton Kanunu’na göre kuru havanın, su buharının ve nemli havanın işgal ettikleri hacimler birbirine eşittir. Bu nedenle salt “v” ile iktifa edilir ve alt simge kullanılmaz.

Psikrometrik diyagramda özgül hacim eğimli düz çizgiler olarak gösterilir.

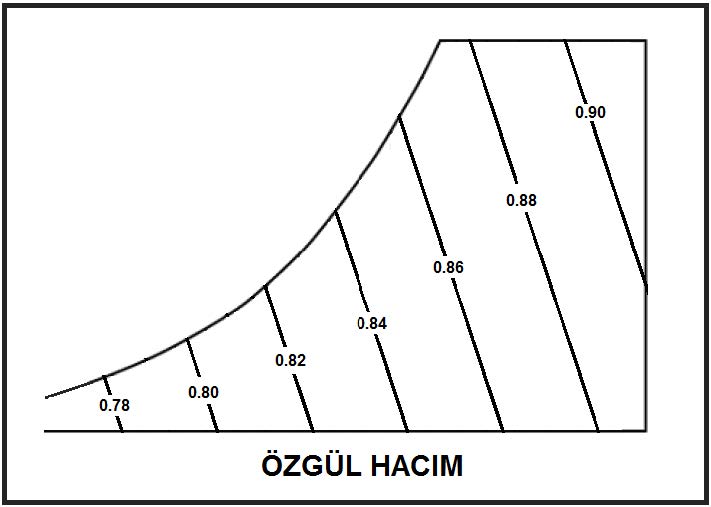
Psikrometrik özgül hacmin tarifi içinde kuru hava ile su buharından başka gazlar dikkate alınmamaktadır. Bu nedenle psikrometrik özgül hacim bilimsel özgül hacim tarifinden az da olsa farklılık içermektedir. Psikrometride özgül hacim nemli havanın hacminin kuru havanın kitlesiyle bölünmesiyle bulunur (m³/kg_da). Ancak diğer bilimsel uygulamalar için özgül hacim tüm elemanları içeren hacmin aynı elemanları içeren birim kütleye bölünmesiyle elde edilir.  İdeal gazları Dalton Kanunu’nun ışığı altında incelediğimizde karışımı meydana getiren kuru havanın ve su buharının aynı hacmi işgal ettiklerini görürüz. Bunu denklem olarak yazdığımızda:

V_da/m_da=V_wv/m_da=V_a/m_da

 Bu denklemde:

V= hacim……………………… m³

             M= kitlesel ağırlık…………kg’dır.

 Bu nedenle aynı denklemi özgül hacim açısından aşağıdaki gibi yazabiliriz:

 v_da=v_wv=v_a

Bu eşitlik eşit kuru termometre şartlarında geçerlidir.

 Özgül hacim ideal gazlarla ilgili denklemlerle de ifade edilebilir:

 P_da. v =R_da. T       

 ve

 P_da= P_bar-P_wv

 Bu iki denklemden hareketle aşağıdaki sonuçlara varırız:

v=(R_da.T)/(P_bar-P_wv)

 v=(287.042)(t_celcius+273.15)/(P_bar-P_wv)

 Daha önce,konu 2.4.4’de aşağıdaki eşitlik bulunmuştu

                          W=0.621945 . p_wv/(p_bar – p_wv)

 Bu eşitliği yukarıdaki denkleme yerleştirdiğimizde aşağıdaki sonuca ulaşırız:

v=(287.042)(t_celcius+273.15).(1 +1.60786W)/P_bar….m³/kg_da

3.8. Mutlak Nem Oranı

 Mutlak nem oranı birim hacimdeki kuru hava içinde bulunan nem miktarıdır. Aynı zamanda kısaca mutlak nem olarak ta ifade edilen bu bulgu şu şekilde ifade edilebilir. Mutlak nem oranı deniz seviyesinden olan yüksekliğin bir fonksiyonudur. Bu husus aşağıdaki hesaplarda da görülmektedir.

W=m_wv/m_da……………………………….(kg_vw/kg_da)

Bu formülde:

                W : Mutlak nem oranı

m_wv: Su buharı kitlesi…………………………..kg_vw

                m_da: Kuru hava kitlesi………………………….kg_da

Psikrometrik diyagramda mutlak nem oranı yatay çizgiler olarak gösterilmektedir.

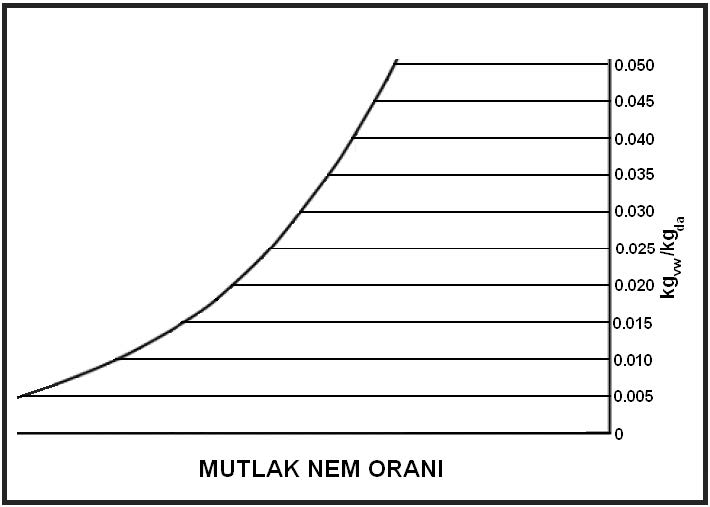
Mutlak nem oranı “W”, su buharı kısmi basıncı “P_wv” ve bağıl nem “rH” arasındaki münasebetleri aşağıdaki gibi belirleyip bu münasebetlerden yola çıkarak mutlak nem oranını hesap yoluyla bulabiliriz. İlk öce ideal gazlarla ilgili genel denklemimizi yazalım, sonra bunlara alt simgeler uygulayarak bu denklemleri su buharı ve kuru hava için tekrarlayalım.

P.V = m.R.T

m= (P.V)/(R.T)

m_da= (P_da.V_da)/(R_da.T_da)

m_wv= (P_wv.V_wv)/(R_wv.T_wv)

R_da= 287.06 J/kg.K)………………   (Bkz. Konu 2.2.4)

R_wv= 461.51 J/kg.K)………………   (Bkz. Konu 2.3.1)

(m_wv/m_da)=W=((P_wv.V_wv)/(R_wv.T_wv))/((P_wv.V_wv)/(R_wv.T_wv))

Bu son denklemde V_wvile V_daDalton kanununa göre eşittirler.Çünkü aynı hacmı paylaşmaktadırlar. Aynı şekilde T_daile T_wvda birbirine eşittir. Bu eşitliklerin birbirini götürmesi halinde formülümüz aşağıdaki şekle döner.

W=((P_wv)/(R_wv.))/((P_wv)/(R_wv))

W=(P_wv.R_da)/(Pda.R_wv)

W=287.06P_wv/461.51P_da

W=0.622 (P_wv/P_da)………………. Bulunur.

P_bar= P_da+ P_{wv……………………….}P_da=P_bar-P_{wv……………}olduğuna göre:

W=0.622 P_wv/(P_bar-P_wv)………………………………bulunur.

Bu son formüle göre mutlak nem oranının, başka bir ifade tarzıyla bir metreküp kuru hava içinde bulunabilecek nem miktarı atmosferik basıncın bir fonksiyonudur. Atmosferik basınç azaldıkça birim kuru hava hacmi içindeki mutlak nem oranı artar. Bu husus Konu 3.9’daki “İrtifaya Göre Doyma Eğrisindeki Değişimler” diyagramında açıkça görülmektedir.

3.9. Buhar Basıncı

Buhar basıncı, atmosferik basıncı meydana getiren kısmi basınçlardan biridir. Bunu daha önceki bahislerde görmüştük. Bu hususu aşağıdaki gibi formülize edebiliriz.

P_bar=P_N2+P_o2+P_Ar+………………………+P_wv

Bu formülde “P_wv” su buharı basıncını, diğerleri ise atmosferi oluşturan sair gazların basıncını ifade etmektedir. Deniz seviyesinde atmosferik basıncın psikrometrik prosesler açısından sabit olduğunun kabul edildiği belirtmiştik. Bu duruma göre deniz seviyesindeki basıncı şöyle de yazabiliriz.

P_bar=P_da+P_wv=101.325 kPa

Bu bağlantıdan iki husus anlaşılmaktadır.

• Kuru havanın basıncındaki artmalar ve eksilmeler buhar basıncını belirler.
• Atmosferik basıncın deniz seviyesinden olan yüksekliğe bağlı olarak değişmesi hem kuru hava kısmi basıncını hem de su buharı kısmi basıncını etkiler.

Kısmi buhar basıncını mutlak nem oranına bağlı olarak şu şekilde hesaplayabiliriz:

W=0.622P_wv/(P_bar-P_wv)…………….(bkz. Bölüm-3, konu 3.8)

P_wv=1.6077W(P_bar-P_wv)

veya

P_wv= W(162.90 – 1.6077P_wv)  …………………….(bulunur)

Deniz seviyesinde doyma noktasındaki buhar basıncı da P_bar’ın yerine 101,325 Pa değerini koymakla bulunur.

Değişik irtifalar için kısmi buhar basıncını değişik bir yöntemle  aşağıdaki gibi hesaplayabiliriz. Bunun için Bölüm-2 , konu 2.4.1’deki basınç hesaplama formülünü “P_wv” formülüne monte etmemiz gerekir.

P_bar=101.325(1 – 2.25577 x 10^-5x Z )^5.2559….dolayısıyla

P_wv=1.6077W(101.325(1 – 2.25577 x 10^-5x Z )^5.2559-P_wv)

Bu formülde “Z” metre cinsinden deniz seviyesinden yüksekliği göstermektedir.

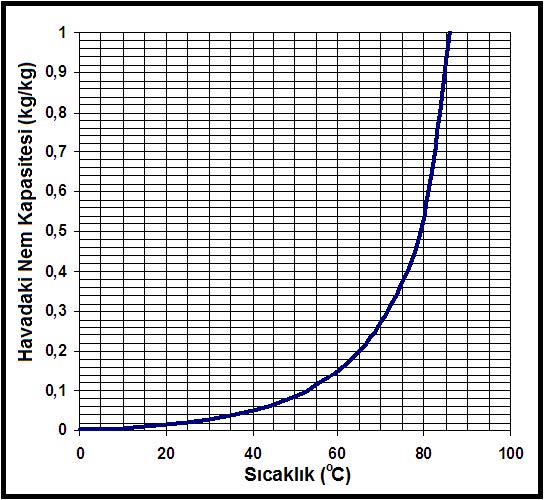
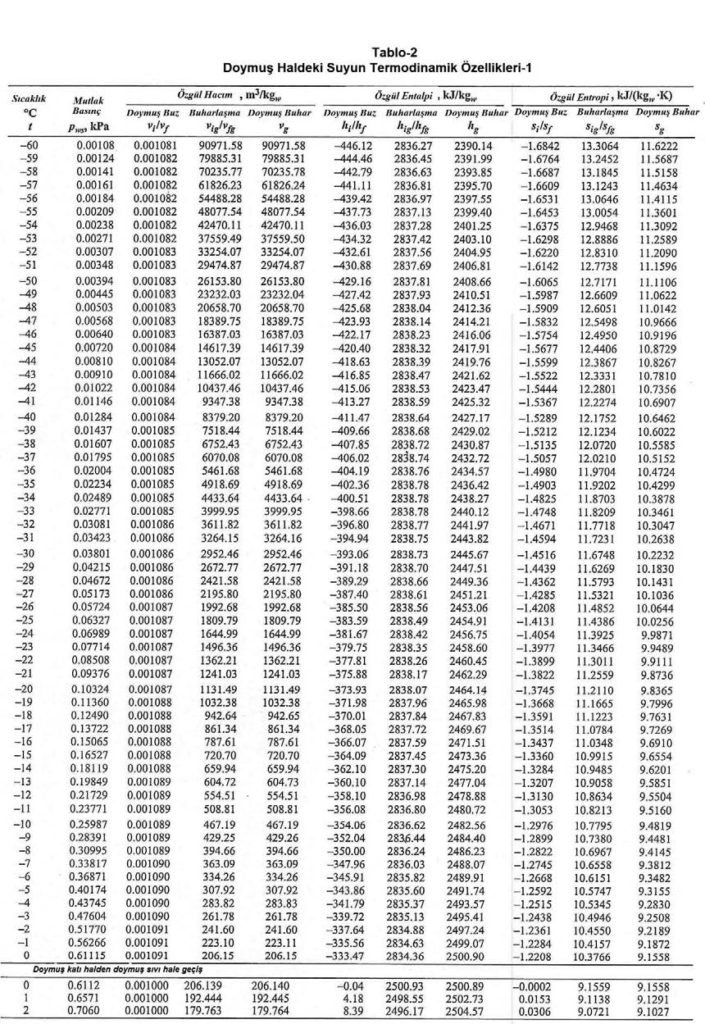
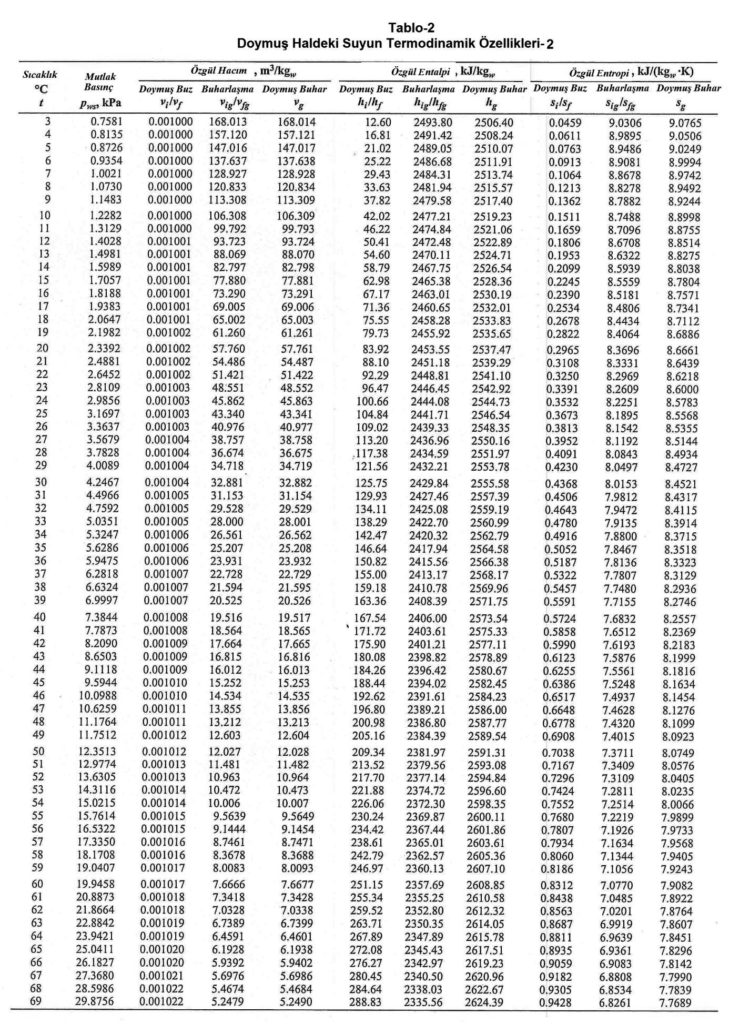
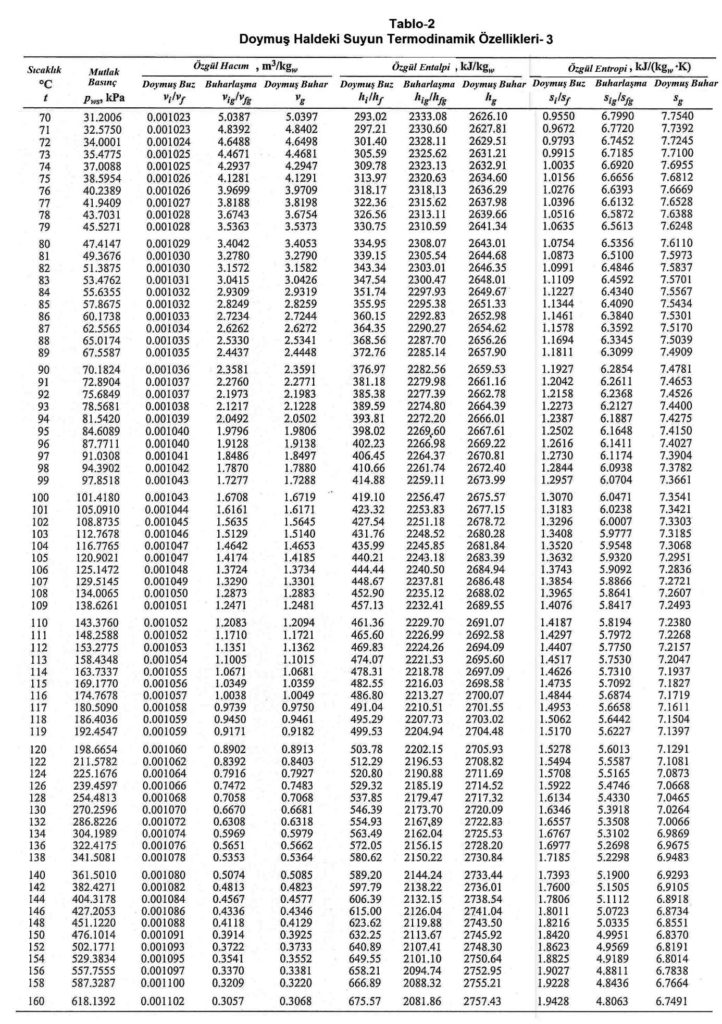
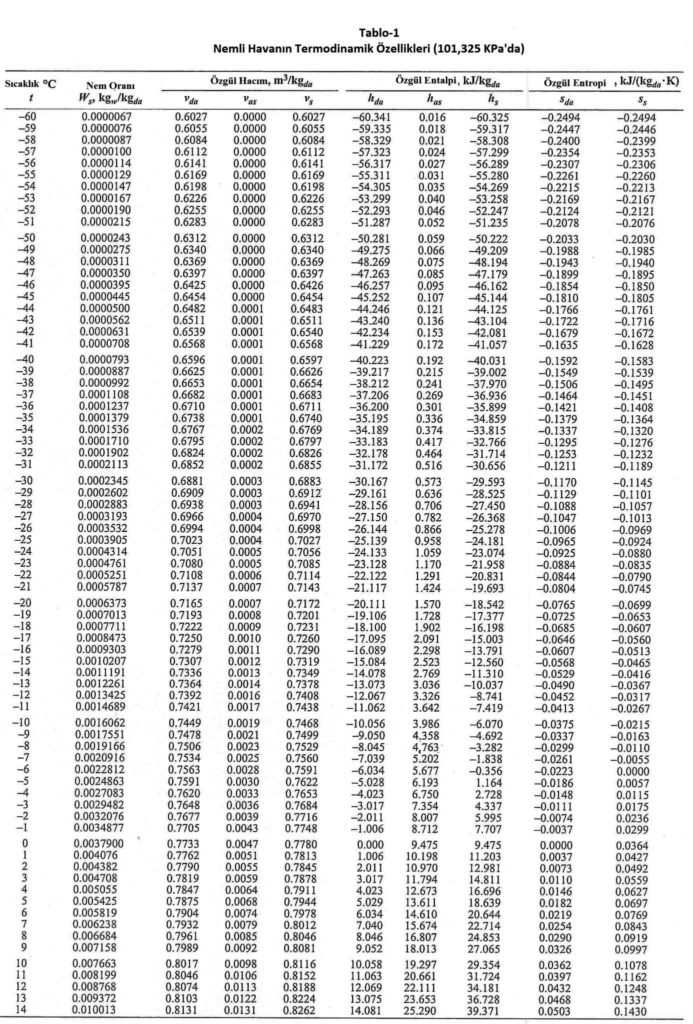
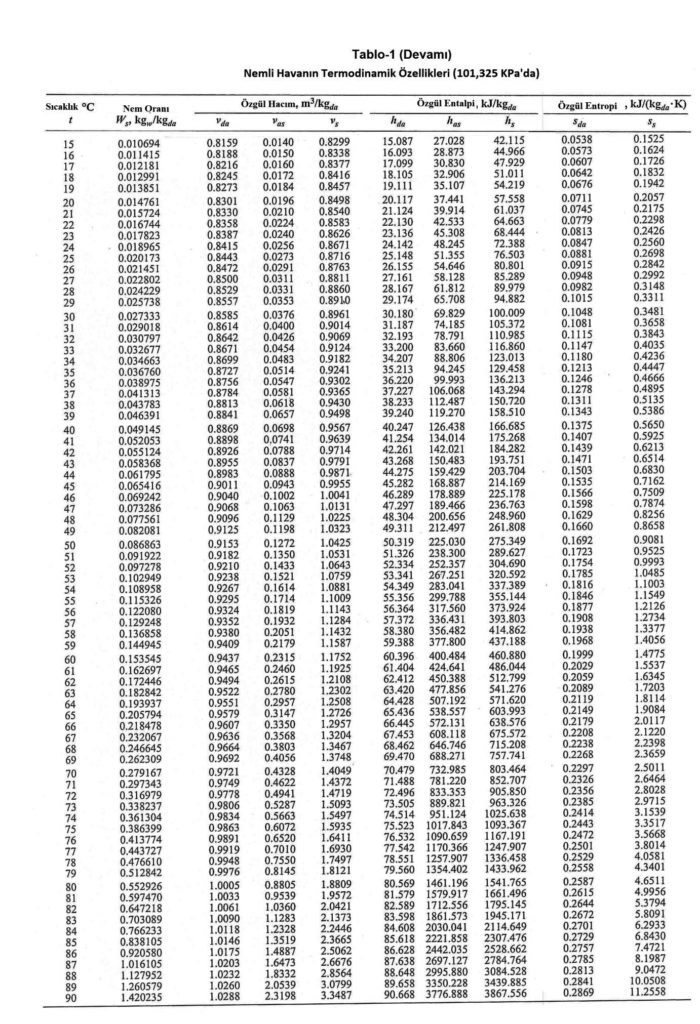
Aynı noktadan hareketle Bölüm-2 konu 2.4.3’deki empirik formülü kullanarak deniz seviyesinde, değişik sıcaklıklardaki doymuş buhar basınçlarını hesapladığımızda aşağıdaki tablodaki değerleri buluruz.

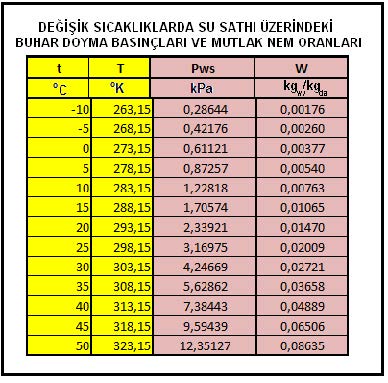
Yukarıdaki tablodan ve formüllerden de görüldüğü gibi buhar basıncı ile mutlak nem oranı birbiri ile birinci dereceden doğru orantılıdır. Bu noktadan hareketle psikrometrik diyagramda buhar basıncı ve mutlak nem çizgilerinin doğrular tarzında, birbirlerinme paralel olduğu, aynı zamanda absise de paralel olduğu anlaşılır. Bu durum aşağıdaki şematik çizimde gösterilmektedir.

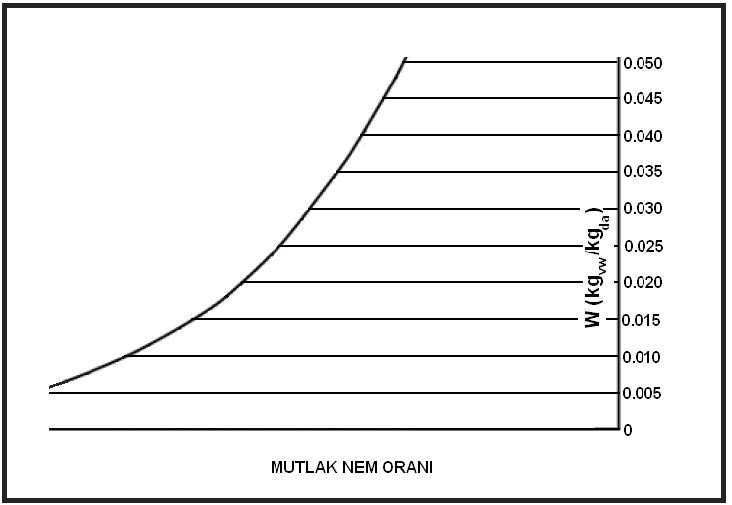
3.10. Özgül Entalpi

Entalpi maddenin yapısında depolanan her türlü enerjinin toplamıdır. Ancak maddelerin kesin entalpilerinin hesaplanması oldukça zordur. Bu yüzden çalışmalarda entalpik değer olarak birim kütledeki maddenin, belirli bir referans noktasından mevcut sıcaklığa yükselebilmesi için gerekli olan enerji ile faz değiştirmesi için gerekli olan enerjinin toplamına denir. Sıcaklık yükselmesi için gerekli entalpi “kJ/kg.” olarak ifade edilir. Keza aynı durum buhar için de gereklidir. Ayrıyeten sabit sıcaklıkta faz birim kitlenin faz değişimi için gerekli ısıya da  prosese bağlı olarak buharlaşma antalpisi veya yoğuşma antalpisi denir.

Birim kütleye sahip maddelerin birim sıcaklık artımı için gerekli ısıyı alabilme kapasitesine “özgül ısı” denir. Önceki yıllarda 1 kilogram suyun sıcaklığının 1^oC artması için gerekli ısı miktarı 1 kCal/^oC.kg kabul edilmiş ve değer arı suyun özgül ısısı olarak kabul edilmişti. Bu kabulden hareket ederek diğer sıvı, katı ve gaz konumundaki maddelerin sabit basınç altındaki özgül ısıları “c_p” belirlenmişti. Günümüzde artık“SI” birimleri kapsamında “kJ/kg.^oC” kullanılmakta ama aynı orantı mantığı devam etmektedir.

Antalpi “h” sembolü ile ifade edilir. Kuru hava için bunu aşağıdaki gibi formülize edebiliriz.

h_da=c_p(Δt)……………………………….kJ/kg

Kuru havanın antalpik ölçümleri için 0^oC noktası referans alınmıştır. Bu sıcaklığıjn altındaki kuru hava antalpileri “-“, üstündekiler ise “+” olarak ifade edilmektedir. Bu açıdan konuya baktığımızda yukarıfaki formül şu şekli alır:

h_da=c_p(t) .……………………………….kJ/kg

Önceki bahislerde, örneğin bu bölümde konu-3.2’de kuru hava ve su buharı için özgül ısı değerleri verilmiştir. Bu değerleri kullanarak kuru havanın entalpisini hesaplamak mümkündür. Ancak psikrometrinin incelediği hava salt kuru hava olmayıp kuru hava ile su buharının karışımından meydana gelmektedir. O zaman havanın antalpisi şu şekilde ifade dilebilir:

h_a= h_da+W.h_wv.……………………………….kJ/kg

Bu formülde:

h_a= Nemli havanın entalpisi……………….kJ/kg

h_da= Kuru havanın entalpisi……………….kJ/kg

h_wv= Su buharının entalpisi…………….….kJ/kg

                       W  = Mutlak nem oranı………………………kg_wv/kg_da

Yaklaşık denklemler olarak, havanın özgül ısısının 1.006 kJ/kg.^oC  kabulü ve “h_wv” değerinin kuru termometre sıcaklığına bağlı  aşağıdaki denklemle hesaplanacağını kabul edersek havanın entalpisini aşağıdaki denklemlerle hesaplayabiliriz (ref. Pyschrometrics, Theory & Practice, ASHRAE, 1996, formül No 1.7.21, 1,7,22 ve 1.7.23=;

h_wv= 2501 + 1.805t   

h_a= 1.006t+W.(2501 + 1.805t)………………………..kJ/kg

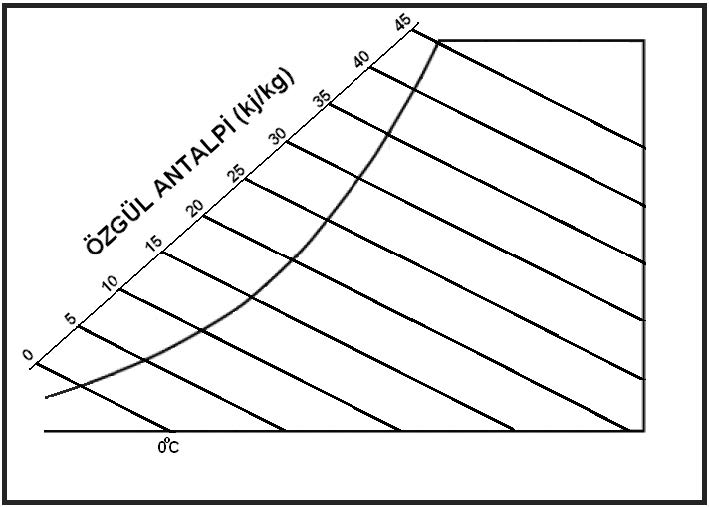
Yaş termometre sıcaklığı ile ilgili bölümde suyun hava içinde buharlaşmasının adyabatik bir proses olduğunu, dışarıdan herhangi bir enerji almadığını, buharlaşmak için gerekli olan ısıyı kuru havadan aldığını belirtmiştik. Başka bir tabirle yaş termometreyi belirleyen işlemlerde su buhar karışımının başlangıçta ve nihayette antalpik değerlerinin aynı kaldığını söylemiştik. Bu nedenle özgül entalpi hatlarının belirli bir eğimde düz çizgiler olduğunu ve bu çizgilerin yaş termometre çizgilerine paralel olduğunu söyleyebiliriz.

Bunun tek istisnası havaya püskürtülen suyun aşırı soğutulması veya aşırı ısıtılmasıdır ki bu durumda proses çizgisi artık sabit entalpi hatlarına paralel olmaz. Bu konuyu 5’inci Bölüm “Psikrometrik Esasların Uygulanması”da detaylı bir biçimde inceleyeceğiz.

 

3.11. Özgül Entropi

Termodinamiğin ikinci yasasına aynı zamanda entropi de denir. Düzensizlik entropi ile eş anlamlıdır. Entropi termal işlemlerde yönü belirler. Örneğin suyun yukarıdan aşağı, ısının sıcaktan soğuğa akması gibi. “s” sembolüyle gösterilen özgül entropi sisteme ilave dilen birim enerjinin “dQ” zamana bölünmesinin integraline eşittir . Gibbs teorisine göre gaz karışımının entropisi onu meydana getiren elemanların entropilerinin toplamına eşittir.

s_a=s_da+ W.s_{wv…………………………………………………………………….}.kJ/kg.^oK

Psikrometrik proseslerde ilmi çalışmalara dışında pek karşılaşmayacağınız bu konuya salt bilgi açısından değinmekle yetineceğiz

2. KURU VE NEMLİ HAVANIN TERMODİNAMİK ÖZELLİKLERİ

2.1 Giriş

Atmosfer azot, oksijen, küçük miktarlarda başka gazlar, su buharı ve duman, polenler, ve havayı kirleten atık gazlardan oluşmaktadır.  Bu karışım bazı kitaplarda “atmosferik hava” veya “nemli hava” olarak adlandırılmaktadır. Biz kitabımızda “atmosferik hava” tabirini hiç kullanmayacağız. Çünkü bu tabir Dünya’mızın tamamını saran, troposfer ve stratosferden oluşan hava kütlesine de verilen isimdir. Halbuki psikrometri yalnızca troposferin alt seviyelerindeki hava ile ilgilenmektedir. Bu nedenle yanıltıcı olabileceğini düşündüğümüz “atmosferik hava” tabiri yerine “hava” tabirini kullanacağız. Bu tabiri “nemli hava”, “kuru hava” ve “su buharı” olarak genişletebiliriz. “Nemli hava”  havadan içerdiği iki elemanla ayrılmaktadır. Bunlar “kuru hava” ve “su buharı”ndan oluşmaktadır. Kuru hava ise içindeki su buharından, havayı kirleten duman, polen ve atık gazlardan arındırılmış teorik bir kavramdır.

Psikrometrinin üzerinde çalıştığı eleman havadır ve bu hava daima iki komponentin, su buharı ile kuru havanın karışımından oluşmaktadır. Bu karışım oranı sabit olmayıp , kuru termometre sıcaklığı, deniz seviyesinden yükseklik gibi şartlara bağlı olarak değişiklik göstermektedir.

2.2 Kuru havanın yapısı

Birinci komponent olan kuru hava hacimsel olarak %78 Azot, %21 Oksijen, %1 Argon, küçük ve değişik oranlarda asgari sekiz ayrı gazın oluşumundan oluşmaktadır.

Yukarıdaki tabloda adı geçen gazların tamamı kendi kritik sıcaklıklarının çok üstündedirler. Bu gazların normal atmosferik şartlarda -100^oC ortam sıcaklığının üstünde yoğuşmaları, havayı oluşturan karışımdan ayrılmaları , dolayısıyla havanın oluşumunda bir değişiklik olması söz konusu değildir. Bu nedenle kuru hava tek bir gaz gibi mütalaa edilebilir, psikrometrik proseslere ve psikrometrik tablonun oluşumuna yönelik hesaplara esas alınabilir. Çünü yıllardır yapılan araştırmalar havanın karışımında ve dolayısıyla moleküler kütlesinde çok küçük değişikliklerin olduğu ve bu değişikliklerin psikrometrik değerlerin oluşumunda çok az etki yarattıkları tespit edilmiştir. 1983 yılında Hyland ve Wexler 28.9645 kg/kmol değerini, 2001’de de Nelson ve Sauer 28.95849 kg/kmol’ü havanın molar kütlesi olan olarak hesaplamışlardır. Bizim verdiğimiz “Temiz Kuru Havanın Yapısı” tablosundaki değerler kullanıldığında ise 28.964 kg/kmol bulunmaktadır.

Hesap tarzı aşağıdaki formülde gösterilmiştir.

∑M.x_i= M_N2.x_iN2+ M_O2.x_iO2+ …… + M_I2.x_iI2       ………………. (kg/kmol)

Yukarıdaki tablonun oluşumunu daha iyi anlayabilmek için kullanılan tabirlerin açıklanması gerekmektedir. Bunlardan ilki moleküler ağırlık ve gaz sabitesidir.

2.2.1. Mole (Mol) ve Moleküler Ağırlık:

Mol ve moleküler kütle, bir maddenin (kitlenin yapısına bağlı olarak ve hangisi daha uygunsa) gram-atom veya gram-molekül ağırlığı, 12 gram karbon izotopundaki atom sayısı kadar temel yapıtaşı içeren bir sistemin madde miktarıdır. Temel yapıtaşları atom, molekül, iyon, elektron ve benzeri taneciklerden oluşan gruplar olabilir ve mol kullanılırken belirtilmelidir. Diğer bir anlatımla Bir mol ağırlığındaki bir maddenin kütlesel ağırlığı 6.022×10²³molekül içermektedir. Bu sayı Avogadro Sayısıolarak bilinmektedir. Bir mol da karbon 12 gram ağırlığındaki Karbon 12 örneğinde bulunan atom sayısı olarak ta tarif edilmektedir.

Önceleri 16 olarak kabul edilen oksijen izotopunun ağırlığı esas alınıyordu. Ancak oksijenin değişik izotoplara sahip olması nedeniyle bu sistem terk edildi. 159/60 yıllarında Uluslararası Teorik ve Uygulamalı Fizik Birliği (IUPAP) ile Uluslararası Teorik ve Uygulamalı Kimya Birliği (IUPAC) karbon izotopunun kullanılması konusunda anlaştılar. Her iki kuruluş kütle numarası 12 olan karbon elementi izotopunun (Karbon-12, C¹²) atom ağırlığı, yani atom kütlesi tam olarak 12 olan bu izotopun esas alınması konusunda anlaştılar. Böylece tüm elementler için birleştirilmiş bir bağıl atomik kütlr skalası belirlenmiş oldu.

2.2.2. Mol Oranı:

“x” ile gösterilen mol oranı bir karışımda bulunan bir gazın mol miktarının o karışımda bulunan tüm gazların mol miktarlarının toplamına bölünmesi ile elde edilen sayıdır. Örneğin iki elemanlı bir karışımdaki birinci elemanın mol oranı aşağıdaki gibidir:

x₁=n₁/(n₁+ n₂)

Burada “n₁” ve “n₂” karışımı oluşturan elemanların her birinin mol miktarlarıdır. Bir gaz karışımını oluşturan eleman sayısı kaç olursa olsun mol oranlarının toplamı daima 1’e eşittir.

x₁+x₂+…………….. x_n= 1

2.2.3. Üniversal Gaz Sabiti:

Universal gaz sabiti ideal bir gazın basıncıyla hacminin basıncıyla çarpımının mutlak sıcaklığa bölünmesiyle elde edilen değerdir. Diğer bir deyişle, basınç ile hacmin çarpımının mutlak sıcaklığa olan oranıdır.

P.V= R . T

“R”  ile gösterilen bu sabite bütün gazlar için geçerli olup değeri:               

8.31441 kJ/(kg.mol.^oK)’dir.

2.2.4. Kuru Hava ve Su Buharının Gaz Sabitleri:

Herhangi bir gazın gaz sabiti, üniversal gaz sabitinin o gazın moleküler ağırlığına bölünmesi ile elde edilir.

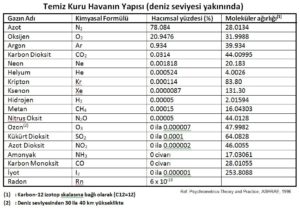
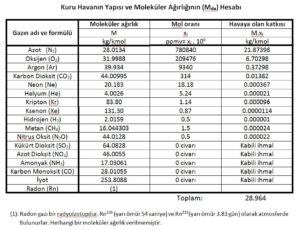
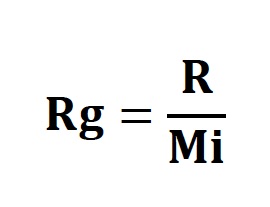 Bu duruma göre azot, oksijen ve kuru havanın gaz sabitleri şu şekilde bulunur:

2.2.5. İdeal Gaz Karışımları :

İdeal gaz karışımları ile ilgili iki temel kanunu hatırlamakta büyük yarar vardır. Bu kanunlar:

• Dalton’un toplanan basınçlar kanunu ve
• Amagat’ın toplanan hacimler kanunu’dur.

Dalton Kanunu’na göre bir gaz karışımının basıncı, karışan gazların karışım sıcaklığında olmaları ve ayrı ayrı toplam hacmi kaplamaları durumunda sahip olacakları basıncın toplamıdır. Amagat Kanunu’na göre de bir gaz karışımının hacmi, karışan gazların karışım sıcaklığı ve basıncında olmaları durumunda yarı ayrı kaplayacakları hacimlerin toplamıdır.

2.3 Su buharı

Psikrometriyi tam olarak anlayabilmek için için H₂O olarak ifade edilen suyun katı, sıvı ve gaz halindeki özelliklerini bütünüyle bilmek gerekir. Birçok madde de olduğu gibi su da üç fazda bulunmaktadır: katı (buz), sıvı (su) ve gaz (buhar veya su buharı). Suyun en büyük özelliği bu her üç fazın da günlük yaşamımızda görülebilmesi ve izlenebilmesidir. Örneğin Yazın bir bardak suya birkaç küp buz koyduğunuzda iki fazı bir arada izlersiniz. Bir müddet sonra bardağın dış sathında su zerrecikleri belirmeye başlar. Bu da yoğuşmakta olan su buharıdır. Bunun nedeni de bardağın dış sathının yoğuşma sıcaklığının altındaki bir sıcaklığa kadar soğumuş olmasıdır. Daha ilerideki bahislerde detaylı olarak ele alacağımız bu konu ile ilgili olarak kısaca şunu söyleyebiliriz: Normal atmosferik şartlarda (STP, Deniz seviyesi, 101.325 Pa basınç) hava içinde bulunabilen maksimum su buharı kuru termometre sıcaklılığna bağlı olarak değişiklikler gösterir. Sıcaklık düştükçe hava içinde bulunabilecek su buharı miktarı azalmaktadır. Bunu da yukarıda bardak örneğinde gördüğümüz gibi satıh yoğuşması ile kendini belli etmektedir. Atmosferik olaylarda ise bu durum kendini yağmur ve kar yağışı olarak belli eder.

Aşağıdaki diyagramda, beher kilogram kuru hava içinde bulunabilecek maksimum su buharı miktarı kilogarm olarak gösterilmektedir.

Suyun faz değişiklikleri termodinamik açıdan büyük önem taşır. Katı halden sıvı hale, buzdan suya dönüşmesine “erime” deriz. 0^oC sıcaklıktaki buzun aynı sıcaklıktaki suya dönüşmesi için gerekli ısı ilavesi 333.47 kJ/kg’dır. Bu işlemin tersi de mümkündür buna da donma deriz.

Keza aynı şekilde suyun sıvı halinin gaz haline, suyun buhar haline dönüşmesi için de ısı ilavesi gerekmektedir. Bu miktar da 15^oC muhit sıcaklığında 2465.38 kJ/kg, 100^oC’ta ise 2256.47 kJ/kg’dır. Bir kilogram suyun buharlaşması  için gerekli ısı miktarı 0^oC’ta 2500.93 kJ/kg ile 100^oC’ta 2256.47 kJ/kg arasında değişir.  Su için logP-H diyagramındaki çan eğrisinin içi buharlaşma prosesini göstermektedir. Burada değişik sıcaklıklarda ve basınçlarda suyun buharlaşması için gereken ısı miktarını hesaplamak mümkündür.

Buzun hiç sıvı hale dönüşmeden gaz haline geçmesi de mümkündür. Bu işleme depozisyon tersine de sublimasyon denir. Bu işlem için gerekli olan ısı miktarı da doğal olarak 0^cC’taki erime ısısı ile aynı sıcaklıktaki buharlaşma ısısının toplamına eşittir.

                    H_sub= h_fg1 + h_fg2=333.47 + 2500.93=2834.4 kJ/kg

Burada:

                     h₌ Antalpi (kJ/kg)

                     h_fg1 = Suyun erime antalpisi (kJ/kg)

 h_fg2= Suyun buharlaşma antalpisi (kJ/kg) ‘dır.

Bu değerler aşağıdaki “Doymuş Haldeki Suyun Termodinamik Özellikleri”nde görülmektedir.

Ref: ASHRAE Fundamentals-2013

Ref: ASHRAE Fundamentals-2013

Ref: ASHRAE Fundamentals-2013

2.3.1. Su buharının molerküler ağırlığı ve gaz sabiti

Su buharı iki hidrojen ve bir oksijen atomundan oluşmaktadır. Bu gazların her birinin Karbon-12 skalasına göre moleküler ağırlıkları aşağıdaki gibidir.

M_H2= 2.0159 kg/kmol

M_O2= 31.9988 kg/kmol

M_{H20 (buhar)}= (1 x 2.0159) + ( 0.5 x 31.9988) 

M_{H20 (buhar)}= 18.01534 kg/kMol

2.4. Kuru hava ile su buharının karışımı

Nemli hava, veya bu kitapta kullandığımız tabiriyle hava su buharı ile kuru havanın ikili karışımından oluşur. Kuru havanın homojene yakın karışımına karşılık su buharı ve kuru havanın karışımından oluşan hava homojen değildir. Sıcaklık ve irtifaya göre farklılıklar gösterir.  Örneğin -40^oC’tan daha düşük sıcaklıklarda hava içindeki su buharı oranı sıfıra yakındır. Sıcaklık ve basınca bağlı olarak çok yüksek değerlere ulaşabilir.  Saturasyon veya doyma noktası gaz durumundaki su (buhar)  ile yoğuşarak sıvıya dönüşmüş sıvı (su) arasındaki dengedir.

Teknik tabir olarak yaygınca kullanılan saturasyon kelimesinin kökeni Latince “satar” kelimesidir; “dolu” veya “doyum” manasına gelmektedir. Ancak biz kitabımızda “doyma noktası”tabirini kullanacağız. Su buharı ile kuru hava atmosferde aynı hacmi paylaşmaktadır. İkisinin kısmi basınçlarının toplamı da atmosferik basıncı oluşturmaktadır.  Doyma noktası da belirli bir basınç ve sıcaklıkta birim atmosferik hacim içinde bulunabilecek maksimum su buharı molekülü miktarını ifade etmektedir. Bu  tabir de “gr_{su buharı}/kg_{kuru hava}” veya  “kg_{su buharı}/kg_{kuru hava}” olarak gösterilir.

 

2.4.1. Standart Atmosfer

Atmosferik havanın sıcaklık ve barometrik basıncı irtifa ile ve buna ilaveten mahallin coğrafik ve meteorolojik koşullarına bağlı olarak değişiklik gösterebilir. Standart atmosfer deniz seviyesinde 15^oC ve 101.325 kPa barometrik basınç olarak ifade edilmektedir. Sıcaklığın troposferde irtifaya bağlı olarak lineer bir değişiklik göstereceği, azalacağı, stratosferde ise sabit olacağı belirlenmiştir.

Aşağıdaki tabloda deniz seviyesinden olan irtifaya bağlı olarak sıcaklık ve basınç değişiklikleri gösterilmektedir.

“Standart Atmosferik Doneler” tablosundaki basınç değerleri aşağıdaki şekilde hesaplanabilir:

p= 101.325 (1-2.25577 x 10^-5x Z)^5.2559……….(kPa)

Sıcaklık değerlerinin hesaplanmasında ise şu formül kullanılabilir:

t= 15 – 0.0065 x Z………………………………………(^oC)

Bu formüller 2013-ASHRAE Handbook Fundamentals’da yer almakta olup hatasız bir şekilde -5000 metre ila 11000 metre irtifa arasında kullanılabileceği belirtilmektedir.”Z” deniz seviyesinden olan yüksekliği belirtmektedir.

 

2.4.2. Havanın Termodinamik Özellikleri:

Aşağıdaki tablolarda havanın termodinamik özellikleri verilmektedir. Hermann, Kretzchmar ve Gatley  tarafından 2009 yılında yayınlanan araştırmadaki formüller esas alınarak hesaplanan havanın termodinamik özellikleri aşağıdaki tablolarda verilmektedir. Bu tabloda kullanılan birimler aşağıdadır

t= “Celcius” skalasına göre sıcaklık. “T”olarak gösterilen “Kelvin”

      skalası ile bağlantısı aşağıdaki gibidir:

    T =t + 273.15……………………… (^oK)

Ref: ASHRAE Fundamentals-2013

Ref: ASHRAE Fundamentals-2013

Tabloda kullanılan sembollerin açıklamaları da aşağıdadır:

W_s= Doyma noktasındaki su buharı miktarının kuru havaya oranı.

       “kg_w/kg_da” olarak ifade edilir.

v_da= Kuru havanın özgül hacmı  “m³/kg_da” olarak ifade edilir.

v_s   = Doyma noktasındaki havanın özgül hacmı “m³/kg_da” olarak ifade

         edilir.

v_as = Doyma noktasındaki kuru havanın özgül hacmı ile kuru havanın

        özgül hacımları arasındaki fark, “m³/kg_da” olarak ifade edilir.

h_da = Kuru havanın özgül antalpisi. “kJ/kg_da” olarak ifade edilir.

h_s  = Doyma noktasındaki kuru havanın özgül antalpisi. “kJ/kg_da” olarak

        ifade edilir.

h_as = Doyma noktasındaki kuru havanın özgül antalpisi ile kuru havanın

        antalpisi arasındaki fark, “kJ/kg_da” olarak ifade edilir.

s_da = Kuru havanın özgül antropisi, “kJ/(kg_da. K)” olarak ifade edilir.

s_s   = Doyma noktasındaki kuru hava ile kuru havanın özgül antropisi

        arasındaki fark, “kJ/(kg_da. K)” olarak ifade edilir.

2.4.3. Doyma Eğrisi ve Hesaplanması

Psikrometrik proses ve hesaplarda doyma eğrisi çok önemli bir yer işgal eder. Bu eğri aynı zamanda su buharı basıncını ve su buharı doyma sıcaklığını da belirler. Birçok eserde bu şartların belirlenmesi için ASHRAE Handbook-Fundamentals’a refere olunur ve oradaki tabloların kullanılması önerilir. Bu tablolar kitabımızda da verilmektedir. Ancak bu değerlerin hesap yoluyla da bulunabileceğinin bilinmesinde fayda vardır. Çünkü mühendislik bir şeyi olduğu gibi kabul etmek değil, bunun nedenlerini bilmek, empirik te olsa formüller ile bu değerlere ulaşabilmektir. Kullandığımız tabloların çoğu da bu yollarla hesaplanarak bulunmuştur. Buna örnek olarak kanal hesap abaklarını, ısıtma ve soğutma hidronik hesaplarında kullanılan boru hesap abaklarını gösterebiliriz.

Günümüzde en doğru yaklaşımları veren formül IAPWS (International Association for the Properties of Water and Steam) -IF97’de belirtilen formüllerdir.  Sıvı haldeki su sathı üzerindeki doyma basıncının sıcaklığa bağlı olarak hesaplanması aşağıdaki formülle belirlenmiştir.

p_ws=1000 x (2 x C/(-B+(B²-4 x A x C)^0.5))⁴………..(kPa)

Bu formülde :

A= Q²+ (N₁x Q) + N₂

B= (N₃x Q²) + (N₄x Q) + N₅

C= (N₆x Q²) + (N₇x Q) + N₈

“Q” değeri ise aşağıdaki formülle hesaplanır:

Q= T + N₉/(T-N₁₀)

T= t_C+273.15 

“t_C” Celcius skalasına göre doyma sıcaklığıdır.      (^oC)

N₁=  1167.05214527670            N₂= -724213.167032060

N₃= -17.0738469400920            N₄= 12020.8247024700

N₅= -3232555.03223330            N₆= 14.9151086135300

N₇= -4823.26573615910           N₈= 405113.405420570

N₉= -0.238555575678490         N₁₀= 650.175348447980

Bu hesap tarzı (0^oC ≤  t_c ≤ 373^oC için geçerlidir. Aynı şekilde “ters denklem” tabir edeceğimiz işlemle de doyma basıncından hareketle doyma sıcaklığını hesaplayabiliriz.

t_Cdp= (0.5 x (N₁₀+ D –((N₁₀+ D)²-4(N₉+N₁₀x D))^0.5))-273.15

Bu formülde :

D= 2G/(-F-(F²-4E x G)^0.5)

E= β²+ N₃x β + N₆

F= (N₁x β²) + (N₄x β) + N₇

G= (N₂x β²) + (N₅x β) + N₈

“β” değeri ise aşağıdaki formülle hesaplanır:

β= ( p_ws/1000)^0.25………………….. (p_ws= kPa)       

2.4.4. Mutlak Nem Miktarının (Nem Oranının) belirlenmesi

Havadaki mutlak nem miktarı (nem oranı) “W” bir kilogram kuru hava içinde bulunan nem miktarının orantı olarak belirtilmesidir. Bu orantı (kg_wv/kg_da) olarak ifade edilir.

Bağıl nem ise belirli bir kuru termometre sıcaklığındaki mutlak nem miktarının aynı sıcaklıkta doyma noktasındaki mutlak nem miktarına oranıdır. Bu tabir “%” olarak ifade edilir.

Mutlak nem miktarının hesaplanmasını da aşağıdaki tar-zda ve Dalton Kanunu’ndan yararlanarak yapabiliriz.

p.V = m . R . T

Bu formülü “m” değerini hesaplamak üzere tekrar düzenlersek:

m = (p . V)/( R . T ) 

 bulunur. Aynı formülü su buharı ve kuru hava için düzenlediğimizde aşağıdaki denklemlere ulaşırız.

m_vw= (p_vws. V_vws)/( R_wv. T )  …….. su buharı için

m_da= (p_da. V_da)/( R_da. T )  ………kuru hava için

 m_vw/m_da=((p_wvs. V_wvs)/( R_wv. T ))/( (p_da. V_da)/( R_da. T )) 

 Dalton Kanunu’na göre su buharı ile kuru hava aynı hacmı paylaşmaktadır. Bu nedenle:

V_vws= V_da

 Keza aynı şekilde her iki gazın ortam sıcaklığı da birbirlerine eşittir. Bu nedenle eşit değerler birbirini götüreceği için denklem aşağıdaki şekle dönüşür.

m_vws/m_da=(p_vws/ R_wv )/(p_da/ R_da) 

 R_wv= 461.52 kJ/kg

R_da= 287.06 kJ/kg

 Bu değerleri yerine koyduğumuzda

m_vw/m_da=0.621945 . p_vw/p_da       bulunur.

p_da= P – P_{vws                                      olduğundan aşağıdaki sonuç formül karşımıza çıkar.}

m_vw/m_da=0.621945 . p_wvs/(p– p_wvs)

 2.4.3 No’lu bahiste doyma nokta sıcaklığındaki buhar basıncını ve o noktadan hareketle doyma noktası sıcaklığının hesaplanacağını incelemiştik. Şimdi de o sıcaklığa tekabül eden mutlak nem miktarını buhar basıncına bağlı olarak nasıl hesaplanacağını görmüş olduk.

 2.4.5. Havanın Özgül yoğunluk ve özgül hacminin belirlenmesi

 P.v_{da_0C}= m . R . T

 Bu denklemde :

P          = Atmosferik basınç, 101325 Pa

v_{da_0C}  = Özgül hacım. 0^oC kuru hava için (m³/kg_da)

m         =Havanın moleküler ağırlığı. 28.964 kg/kmol

R          = Üniversal gaz sabiti . 8314.41 J/(kmol.K)

T          = havanın sıcaklığı ( ^oK)

Değerleri denklemde yerlerine koyup, “v_{da_0C}”için çözdüğümüzde:

v_{da_0C}=((8314.41)x(273.15 + 0))/(28.964×101325)

 v_{da_0C}= 0.773851 …………………………….  (m³/kg_da-0C)

 Havanın özgül yoğunluğu: δ_{da_0C}= 1/ v_{da_0C} olduğuna göre:

δ_{da_0C}= 1/ 0.773851=1.2922 … (kg_da-0C/m³) bulunur.

Bu formülü genelleştirdiğimiz zaman, derğişik sıcaklıklardaki kuru havanın özgül hacmini aşağıdaki formülle hesaplayabiliriz.

v_da= 0.0028333 (273.15 + t_da)

 Kuru havanın hesapla bulunan özgül ağırlığına aynı sıcaklıktaki doyma noktasındaki havanın içinde bulunan su buharının ağırlığının ilavesi ile doyma noktasındaki havanın özgül hacmi ve özgül ağırlığı bulunur.

δ_a= δ_da+ W_wv