Kategori: Psikrometri 1 Kitabı

8. TABLOLAR ve DİYAGRAMLAR

 

SEMBOLLER

 

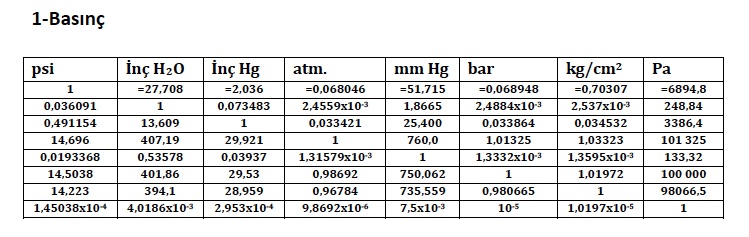
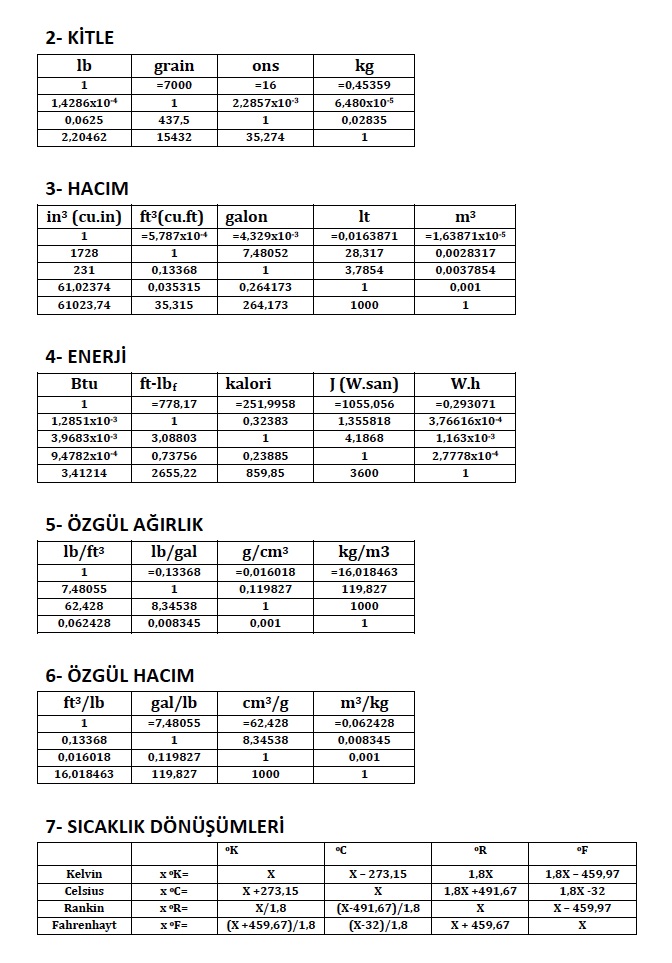
BİRİM DÖNÜŞÜMLERİ 

Birim dönüşümleri için çarpımlar 

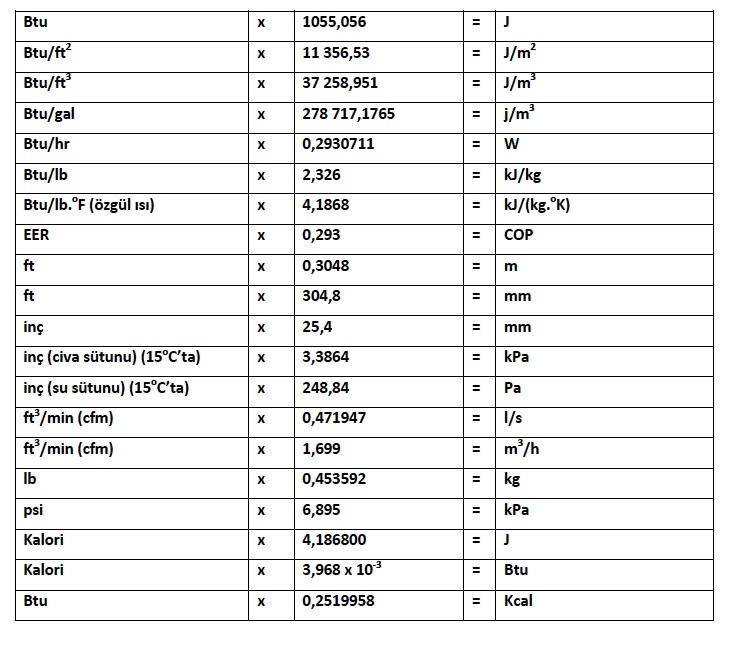
Birim dönüşümleri için çarpımlar

Referanslar

1. ASHRAE Handbook of Fundamentals,

2. Psychrometrics, Theory and Practice, ASHRAE, 1996

3. Understanding Psychrometrics, Donald P. Gatley, ASHRAE, 2013

4. Handbook of Air Conditioning System Design, Carrier Co.,McGraw Hill 1965

5. Trane Air Conditioning Manual, 1974

6. Termodinamik, Y.A.Çengel, Michael A.Boles, McGraw-Hill/Literatür Yay, 1996

7. Isı ve Kütle Geçişinin temelleri, F.P.Incropera,D.P.DeWitt,Literatür Yay 2010

8. Isıtma+Klima Tekniği, 97/98, Recknagel-Sprenger Schramek, TTMD  2003

9. Psychrometric Chart Celebrates 100th Anniversary. D.P.Gatley, ASHRAE Journal 11, 2004

10. Air Conditioning Psychrometrics, A. Bhatya, CED engineering.com

11. Construction of Generalized Chart for Different Pressures, He-Sheng Ren

12. Understanding Humidity and Calculating Humidity Parameters, B.Pragnell

13. IAPWS, Industrial Formulation, 1997 007

14. Engineering Thermodynamics, N.J.Morgan, H.N.Shapiro

15. Steam Tables, Keenan & Keyes, Wiley 969

16. Thermophysical Properties of Humid Air, M. Conde Engineering, Zurich 2007

7. ÖRNEKLER

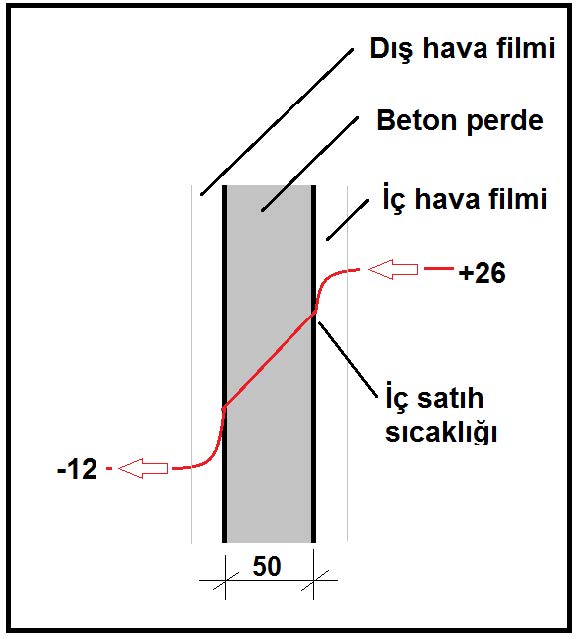
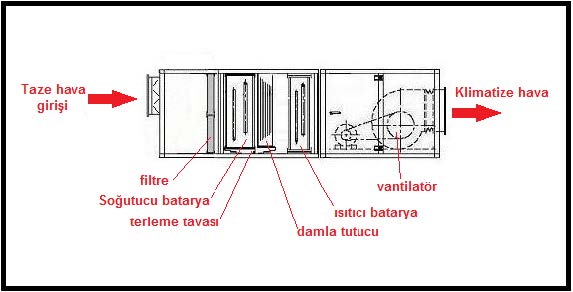
 7.1.YÜZEY KONDANSASYONU ve ENGEL OLMAK  İÇİN GEREKLİ İZOLASYON KALINLIĞI.

 Nem oranı yüksek ve/veya dış hava sıcaklığı çok düşük yerlerde duvar ve pencerelerde yüzey kondansasyonu çok sık karşılaşılan bir sorundur. Buna mani olmak için bu satıhlara paralel sıcak hava üflenir. Bu uygulama bir çözümdür, ancak enerji sarf etmeden de bunun önlenmesi mümkündür. Bu da bir etüd gerektirir. Prosedürü şu şekilde özetleyebiliriz:

• Önce mahal şartları dikkate alınarak oda çiy noktası“DP” psikrometrik diyagram üzerinden belirlenir.
• Separasyonun (duvar, pencere, tavan vb.) satıh sıcaklığı hesap yoluyla bulunur. Bu sıcaklık oda çiy noktası “DP” ile karşılaştırılır. Eğer hesaplanan sıcaklık “DP”den düşükse satıh kondansasyonu oluşacaktır.
• Bu durumda duvar ısı iletim katsayısı izolasyon malzemeleri de dikkate alınarak yenilenir. Yeni hesaba göre satıh sıcaklığı tekrar hesaplanır. Bulunan sıcaklık “DP”den büyükse çalışma başarılı olarak neticelenmiştir. Eğer değilse izolasyon kalınlığı arttırılarak veya cinsi değiştirilerek takrarlanır.

Bunu bir örnekle izah edelim.

Oda şartlarımız 26^oC, %65 rH, dış hava şartlarımız da -12^oC (örneğin Ankara) olan bir mahalde dış duvar kalınlığı 50mm sıvasız beton perdedir. Kondansasyon olup olmayacağını, eğer oluşuyorsa gerekli izolasyon kalınlığını hesaplayın:

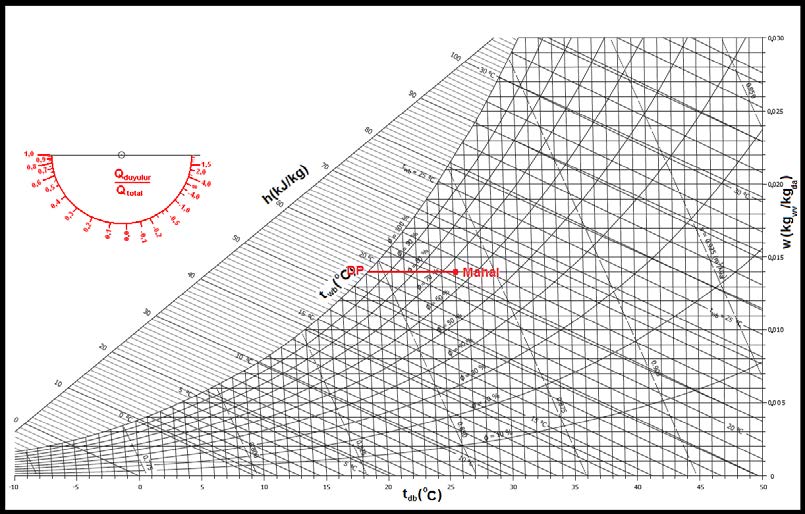
Psikrometrik diyagramdan 26^oC, %65 rH oda şartları için doyma noktası “DP” 19,3^oCKT olarak bulunur.

İkinci olarak beton perde duvarın ısı iletim katsayısını hesaplayalım:

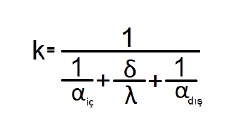
K=Isı iletim katsayısı (W/^oK.m²)

α_iç=İç hava film katsayısı (23,50 W/^oK.m²)

α_dış=Dış hava film katsayısı (8,15 W/^oK.m²)

δ = duvar kalınlığı (0,05 m)

λ = ısı iletkenliği (0,80 W/m.^oK)

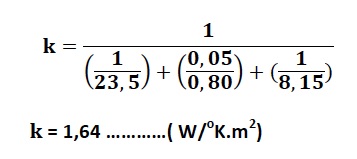
Üçüncü olarak ısı denklemini kuralım. Denklem 1 metrekare yüzey alanı için yapıdığından denklem alan ölçüsü “F” bulunmayacaktır.

q₁= k₁(t_iç-t_dış)

q₁= 1,64 x 38 =62,32 W/m² 

Dördüncü olarak iç sathın sıcaklığını hesaplamak için ısı eşitlik denklemini kuralım.

q₂= k₂(t_satıh-t_dış)

 q₁= q₂

 k₁(t_iç-t_dış)= k₂(t_satıh-t_dış)

 62,32= k₂(t_satıh-t_dış)

Beşinci olarak “k₂” diye adlandırdığımız, iç hava filmini dikkate almayan ısı iletim katsayısını hesaplayalım

 

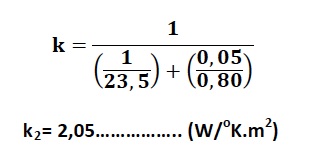
 Bulduğumuz bu değeri ısı eşitliği denklemindeki yerine koyarak satıh sıcaklığını bulalım.

k₁(t_iç-t_dış)= k₂(t_satıh-t_dış)

62,32= 2,05 (t_satıh+12)

t_satıh= +18,4 < 19,3^oC

Bulduğumuz bu sonuca göre satıhta terleme olacaktır. Terlemeye mani olmak için iç sathı poliüretanla izole edeceğimizi kabul edelim ve izolasyon kalınlığını hesaplayalım.

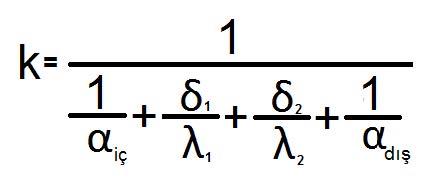
Bu formülde ,

δ = izolasyon kalınlığı (X m)

λ = ısı iletkenliği (0,03 W/m.^oK)

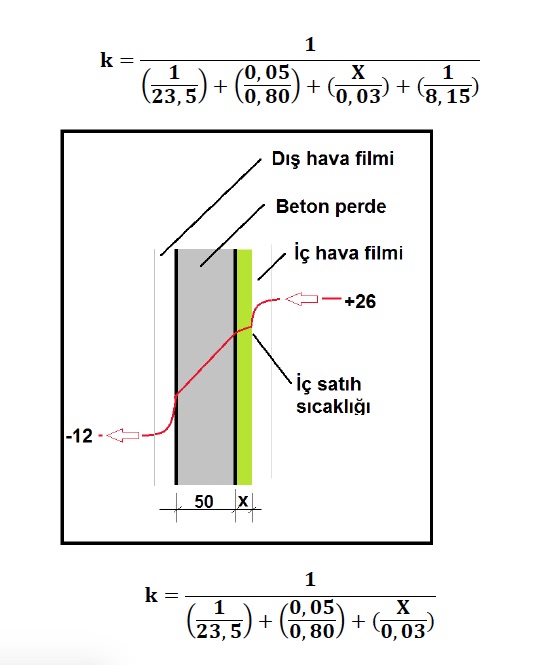
k₁(t_iç-t_dış)= k₂(t_satıh-t_dış)

k₁(26+12)= k₂(19,3+12)

38k₁= 31,3k₂

X= 0,0025m (≃30mm) izolasyon kalınlığı bulunur.

Aynı işlemi pencereler ve vitrin camlar için de yapabiliriz.

sıcaklığı sabittir. Üflenen hava miktarı mahallin maksimum yaz (soğutma) yüküne göre belirlenir. Minimum hava debisi IAQ’ya bağlı olarak mahallin minimum hava debisine, örneğin içerideki insan sayısı ile beher kişi için gerekli olan taze hava miktarının çarpımına eşittir.

İki değişik türde VAV uygulaması yapılmaktadır.

• Yaz ve kış uygulamalarının tümünde değişken hava debisi

7.2. Değişik ve Sabit Sıcaklıklardaki Suyun Havaya püskürtülmesi.

Bölüm-5, konu 5.5.1’de havanın su ile nemlendririlmesi incelenmişti. Ku konuda dışarı ile ısı alış-verişi olmaması nedeniyle gerekli buharlaşma ısısının dahilden, yani su ve havadan karşılanacağı, bu adyabatik proses sonucu su sıcaklığının adyabatik doyma noktası sıcaklığına eşit olacağı, havanın adyabatik soğuma neticesi, verim oranında bu sıcaklığa yaklaşacağı anlatılmıştı. Bu uygulamalar, yukarıda da belirtildiği gibi dışarıdan herhangi bir ısı (sürekli ısıtma veya soğutma) ilavesi yapılmaması durumda geçerlidir. Ancak bu tam olarak ısı ilavesi durumunda doğru değildir. Havanın püskürtülen su sıcaklığına yaklaşacağı doğrudur, ancak proses artık bir adyabatik proses değildir. Bu konunun detaylı incelenmesi başka bir kitabın konusudur. Biz burada kısa bir bilgilendirmeyle yetineceğiz.

Bu işlemler iki değişik uygulama için aşağıda gösterilmiştir.

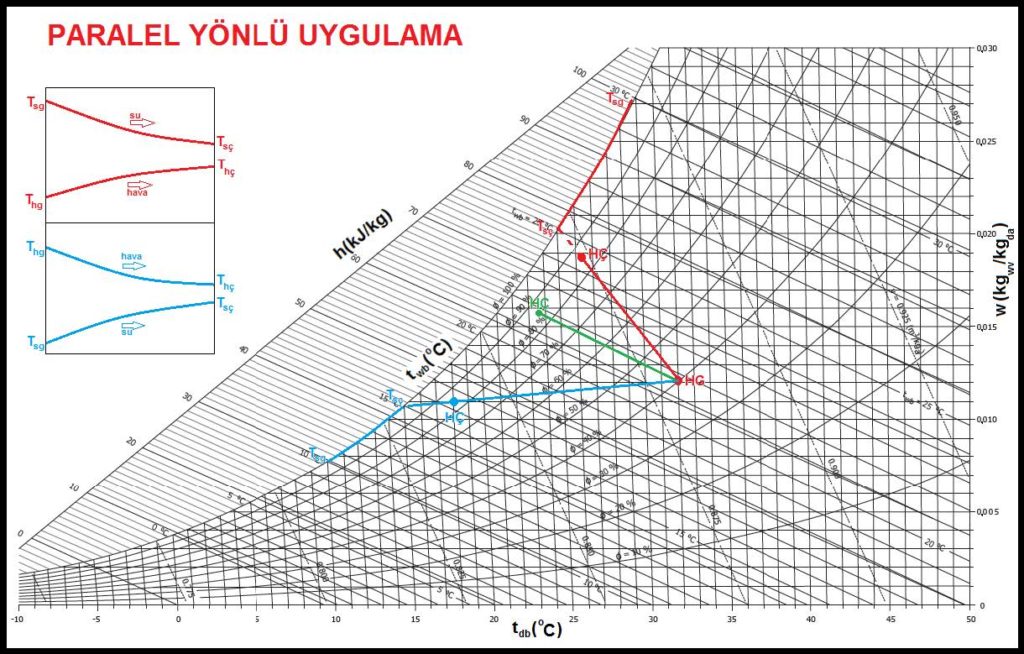
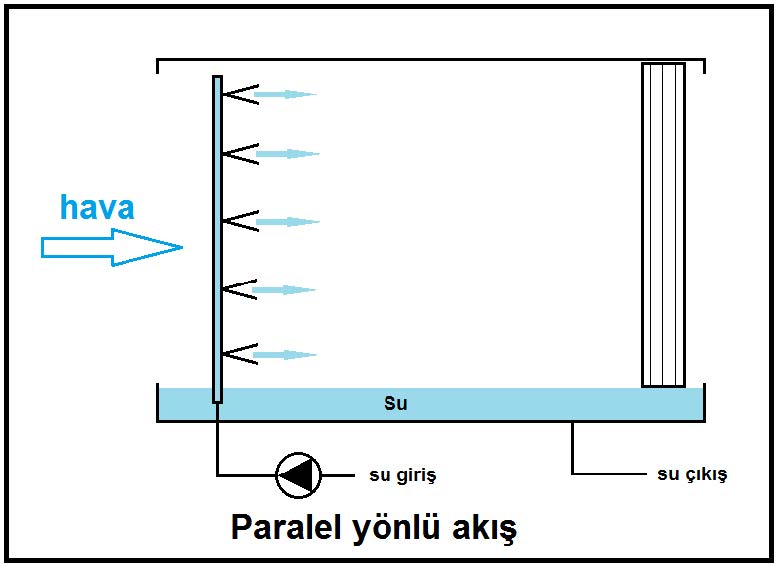
Bu uygulamalardan birincisi paralel yönlü uygulamadır. Buna örnek olarak hava yıkayıcılı klima santralarındaki paralel yönlü püskürtmeyi gösterebiliriz. Ancak bu uygulamanın tek farkı nemlendiriciye gelen suyun devamlı ısıtılması veya soğutulmasıdır.

Paralel yönlü nemlendirici aşağıda şematik olarak gösterilmektedir.

 

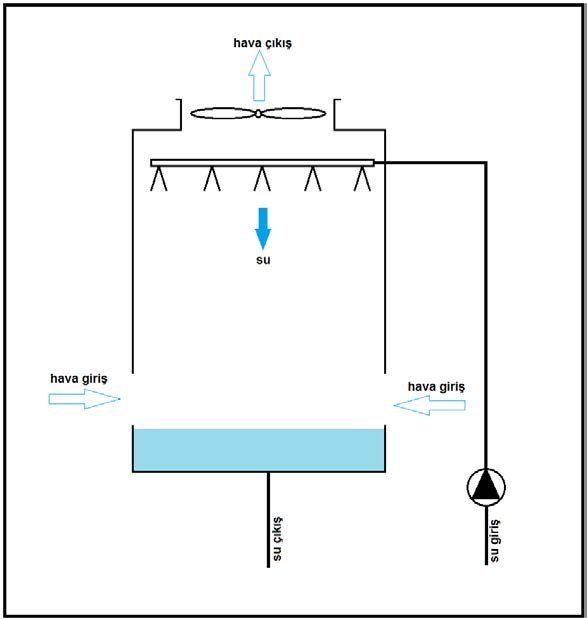
Diğer bir uygulama da ters yönlü akış prensibine göre yapılan uygulamalardır. Bu uygulamaların en tipik örneği dik tip su soğutma kuleleridir. Bunun psikrometrik diyagramını ve diyagramatik çizimini aşağıda görüyorsunuz.

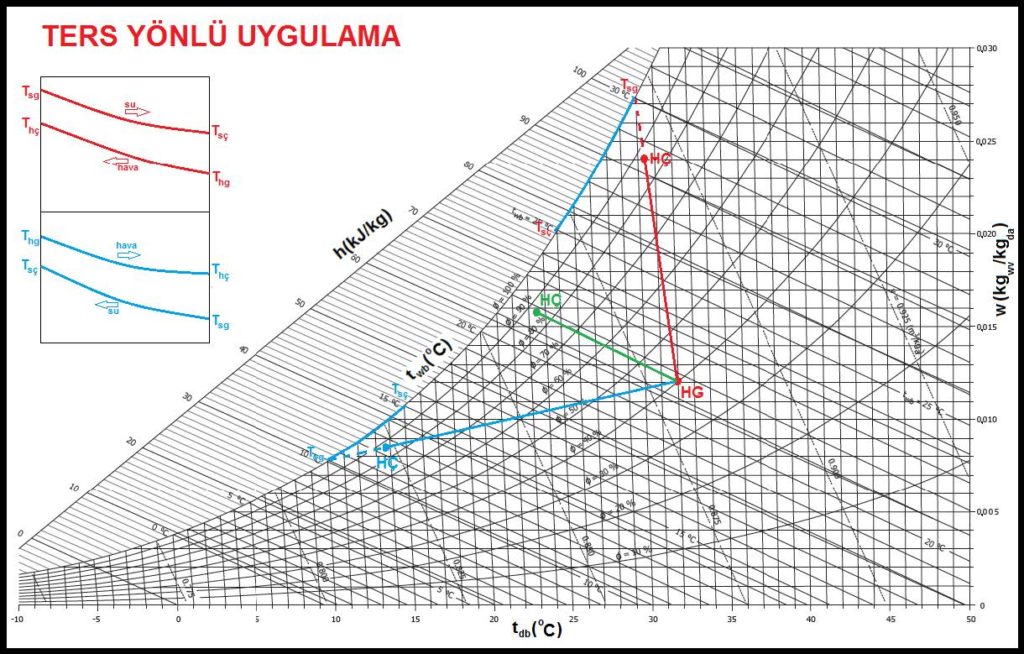
Her iki diyagramda da mavi çizgiler soğutulmuş su ile, kırmızı çizgiler ise ısıtılmış su ile gerçekleştirilen prosesleri temsil etmektedir. Yeşil hat ise herhangi bir ısı ilavesi olmaksızın gerçekleştirilen adyabatik prosesi göstermektedir.

 

6. KLİMA UYGULAMALARININ PSİKROMETRİK OLARAK İNCELENMESİ

6.1. SOĞUTMA YÜKÜNE BAĞLI OLARAK HAVA DEBİSİNİN TAYİNİ

 Bir mahallin soğutma yükünü karşılamak için gerekli hava debisi o mahallin duyulur ısı kazancına bağlıdır. Bunun nedeni de duyulur ısı yükünün kuru termometre sıcaklığının değişimi ile karşılanmasından kaynaklanmaktadır. Bu nedenle mahal için gerekli hava debisi mahallin duyulur ısı kazancının üflenen sıcaklık fakı ile havanın sabit basınçtaki özgül ısısı ve özgül ağırılığının çarpımına bölünmesi ile elde edilir.

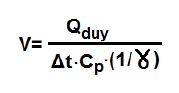
Bu işlemde:

Q_duy= Mahallin duyulur ısı kazancı   (kJ/h)

ɤ    = havanın özgül hacmi  (m³/kg)

Δt   = Oda kuru termometre sıcaklığı ile üflenecek klimatize hava

Arasındaki sıcaklık farkı . Genelde 8^oC ila 10^oC alınır.

C_p    = havanın sabit basınçta özgül ısısı ( 1.00483 kJ/kg) (Havanın özgül ısısı ile ilgili hususlar Bölüm-1, konu 3.2’de geniş olarak anlatılmıştır.)

Bundan sonra yapılacak işlem psikrometrik diyagram üzerine “t_RA”ve “t_sa” değerlerini izotermler halinde işlemektir. İkinci işlem ise “RSHR”ye bağlı proses hattının çizilmesidir.

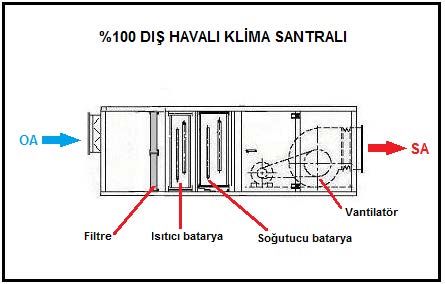
Sisteminiz %100 dış hava ile çalışacaksa “SA” konumu ile “OA” konumu bir doğru ile birleştirmek yeterlidir. Elde edeceğiniz doğru klima santralındaki soğutma prosesidir. Bu hattın eğimi “ESHR” ye eşittir ve hattın doyma eğirisini (%100 bağıl nem eğrisini) kestiği nokta da “ADP” olarak tanımlanan cihaz çiy noktasıdır.

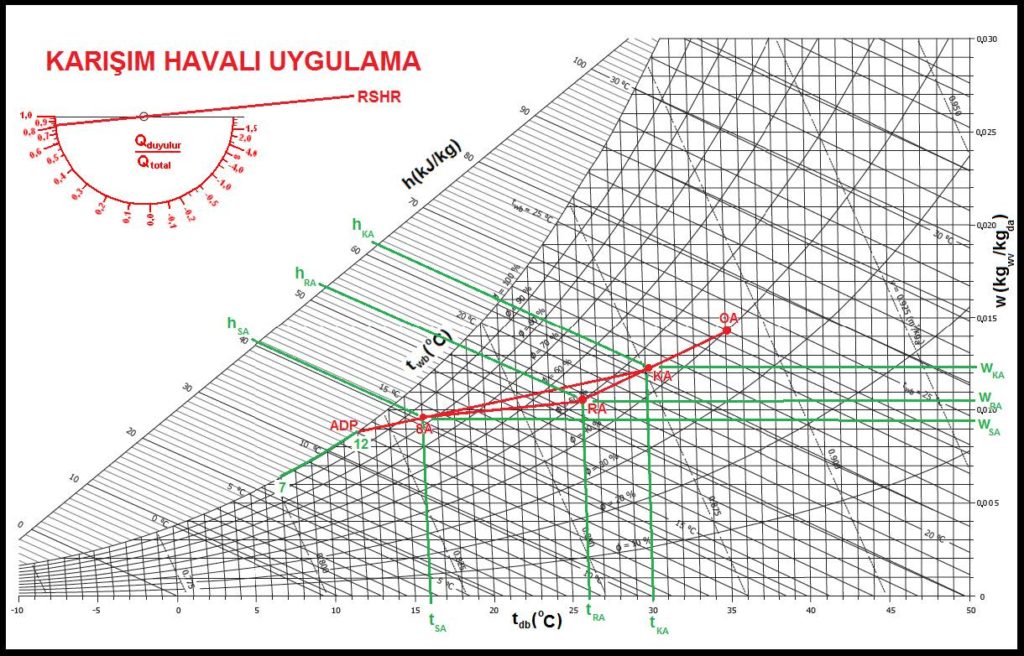
Eğer sistem karışım havası ile çalışacaksa önce “RA” ile “OA” konumlarını düz bir çizgi ile birleştirip bu hat üzerinde karışım noktasını bulmanız gerekir. İkinci işlem ise bulunan bu “KA” noktasını “SA” ile birleştirmektir. Karışım havalı uygulamalardaki soğutma prosesi çizginiz bu olacaktır. Bu çizginin de doyma eğrisini kestiği nokta “ADP” noktanızdır. Bu noktayı soğutucu akışkan dönüş sıcaklığı olarak alabilirsiniz.

%100 dış havalı uygulama aşağıdaki psikrometrik diyagramda görülmektedir.

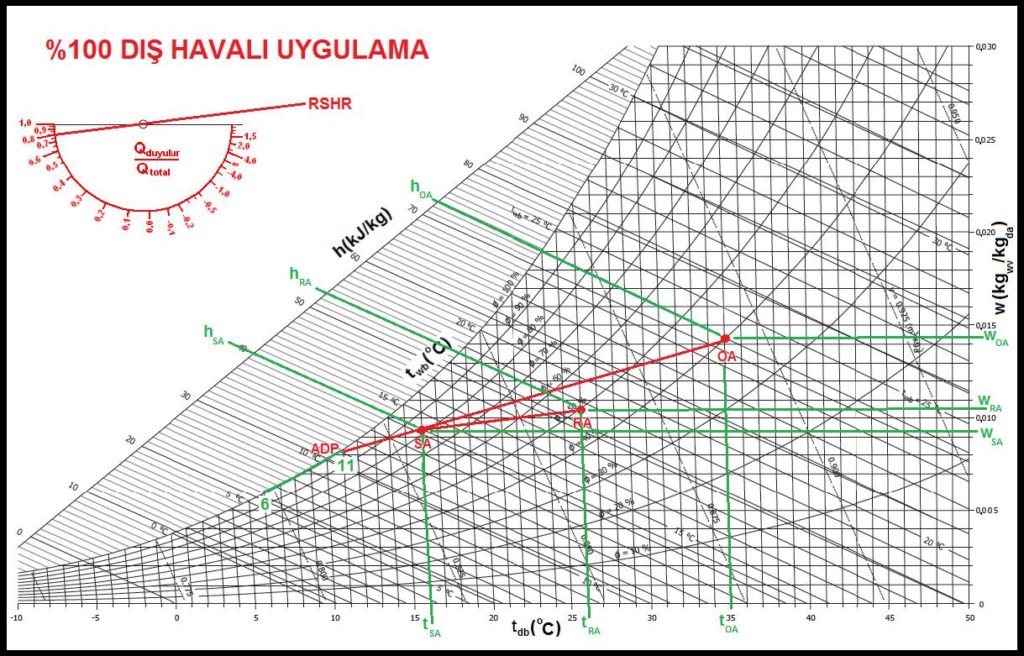
Bu uygulamada:

Q_duy-oda= V.(1/ɤ)c_p(t_RA-t_SA)
Q_giz-oda= V.(1/ɤ)(w_RA-w_SA).h_fg
Q_top-oda= V.(1/ɤ)c_p(t_RA-t_SA) + V.(1/ɤ)(w_RA-w_SA).h_fg
RSHR= Q_duy-oda/ Q_top-oda

Q_duy-sist= V.(1/ɤ)(h_OA-h_SA)= V.(1/ɤ)c_p(t_OA-t_SA)
Q_giz-sist= V.(1/ɤ)(w_OA-w_SA).h_fg
Q_top-sist= V.(1/ɤ)c_p(t_OA-t_SA) + V.(1/ɤ)(w_OA-w_SA).h_fg
ESHR= Q_duy-sist/ Q_top-sist

olmaktadır.

“ADP” sıcaklığı 11^oC olduğu için tercih edilen soğutucu akışkan, istenen “ESHR” soğutma prosesi eğrisini sağlayabilmek için 5/11^oC veya  6/11^oC olmalıdır.

Aşağıdaki psikrometrik diyagramda da karışım havalı bir uygulama görülmektedir. Bu uygulama için aynı denklemlerle mahal ve sistem yüklerini bulabiliriz. Ancak sistem karışım havalı olduğu için sistem yükünün hesabında “OA”ların yerini “KA”lar alacaktır.

 Q_duy-oda= V.(1/ɤ)(h_RA-h_SA)= V.(1/ɤ)c_p(t_RA-t_SA)
Q_giz-oda= V.(1/ɤ)(w_RA-w_SA).h_fg
Q_top-oda= V.(1/ɤ)c_p(t_RA-t_SA) + V.(1/ɤ)(w_RA-w_SA).h_fg
RSHR= Q_duy-oda/ Q_top-oda

Q_duy-sist= V.(1/ɤ)(h_KA-h_SA)= V.(1/ɤ)c_p(t_KA-t_SA)
Q_giz-sist= V.(1/ɤ)(w_KA-w_SA).h_fg
Q_top-sist= V.(1/ɤ)c_p(t_KA-t_SA) + V.(1/ɤ)(w_KA-w_SA).h_fg
ESHR= Q_duy-sist/ Q_top-sist

ADP konumu 12^oC olması nedeniyle seçilen soğuk su rejimi 7/12^oC’dir.

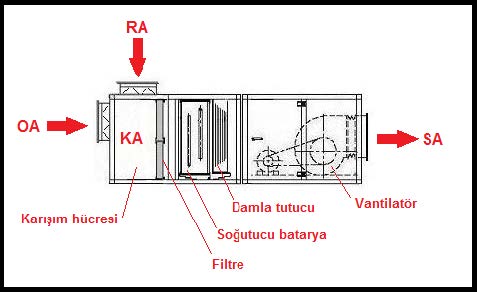
Bu prosese uygun klima santralı aşağıda gösterilmektedir. Şemtik çizim üzerine, takip kolaylığı açısından psikrometrik prosesteki tanımlar da işlenmiştir.

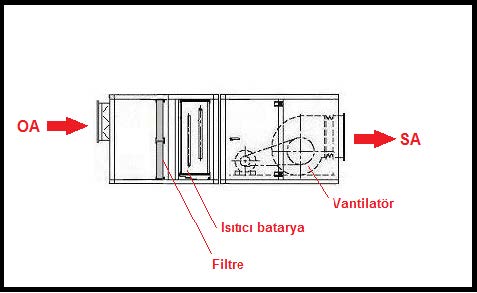
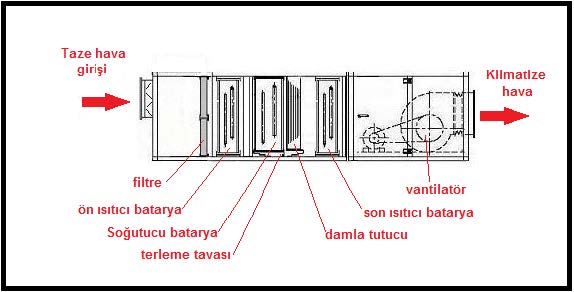
6.2. KIŞ UYGULAMASI İÇİN HAVA DEBİSİ VE ISITMA YÜKLERİNİN TESPİTİ-1, NEMLENDİRMESİZ ve SU İLE NEMLENDİRMELİ ÖRNEKLER.

 Genelde kış uygulaması için gerekli hava debisi yaz klima yükü esas alınarak belirlenen hava debisine eşit alınır. Ancak daha yüksek üfleme sıcaklıklarının arzu edilmesi, veya dış hava yükünün fazla olması gibi  durumlarda enerji tasarrufu açısından değişik debili uygulamalara gidilebilir ve kış uygulamaları için daha düşük hava debileri seçilebilir. Bu tip uygulamaların çift devirli veya frekans konvertörlü vantilatör ve aspiratörlerin kullanılması suretiyle gerçekleştirilmesi mümkündür. Biz örneğimizde sabit hava debili bir klima santralı için psikrometrik prosesi belirlemeye çalışacağız.

Kış uygulamasında karşımıza çıkan en büyük sorun nemlendirmenin yapılıp yapılmayacağıdır. Nemlendirmeye olan ihtiyacı o mahaldeki gizli ısı kazançları belirler. Eğer gizli ısı kazançları neticesi %35’in üzerinde bir bağıl nem “rH” gerçekleştirilebiliyorsa ve özel bir gereksinim yoksa nemlendirme yapılmayabilir (Bkz. Konu 5.7. Oda Efekti) . Ancak %35’in altındaki bağıl nem oranlarının insanları rahatsız edeceği, ciltte ve burun mukozasında kurumalara neden olacağı için nemlendirme yapılmalıdır. Biz sistemlerimizde her ikisini de ele alacağız.

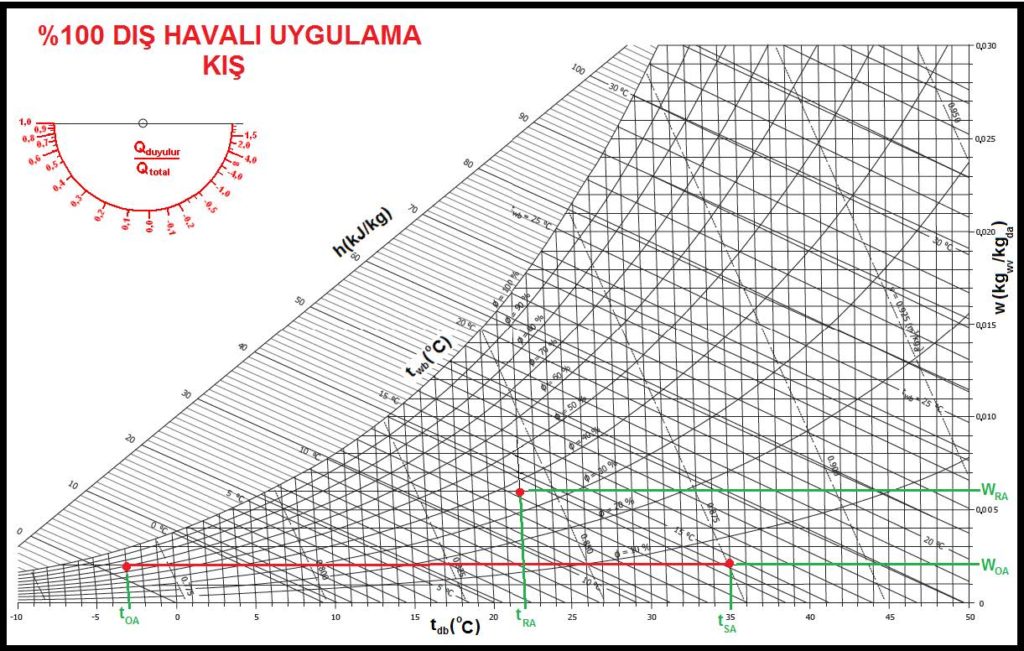
Yukarıdaki örneğimizde 510 harici havalı bir kış kliması uygulaması gösterilmektedir. Bu uygulamada “t_OA-t_RA” arası ısıtma işlemi dış havanın mahal şartlarına kadar ısıtılmasını, “t_RA-t_SA” arasındaki işlem ise mahallin ısı kaybını karşılamak için mahal şartlarına kadar ısıtılmış havanın “SA” şartına kadar aşırı ısıtılmasını içermektedir.

Q_DH= V.(1/ɤ)c_p(t_OA-t_RA)………… dış havanın oda şartlarına kadar ısıtılması

Q_Kış= V.(1/ɤ)c_p(t_RA-t_SA)………… mahal ısı kaybı

∑Q_Kış= Q_DH+ Q_Kış…………………. Toplam ısıtma yükü

Bu uygulamada oda efekti neticesi istenen mahal şartları olan 22^oCKT, %35 rH’ın elde edileceği,  dolayısıyla mahalde birim hava debisi için “W_OA-W_RA”kadar gizli ısı kazancı olduğu varsayılmıştır.

Diğer bir uygulama da ısıtılan dış havanın mahal konfor şartını temin etmek amacıyla nemlendirilmesidir. Bu uygulamada mahalde gizli ısı kazancı olmadığı veya ihmal edilebilecek bir düzeyde olduğu varsayılmıştır.

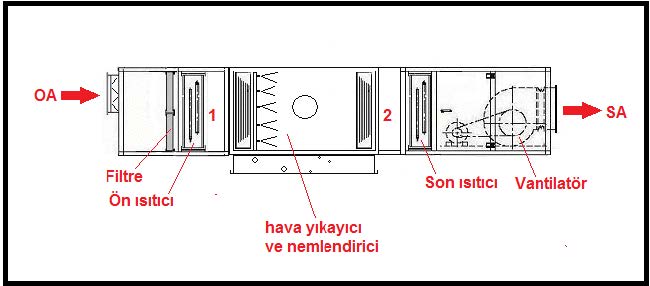
Bu prosese uygun klima santralının şematik çizimi aşağıda gösterilmektedir.

Nemlendirme işlemi, konu 5.5’de anlatıldığı gibi iki şekilde yapılabilmektedir.

• Su ile nemlendirme
• Buhar ile nemlendirme

Biz bunlardan önce su ile nemlendirmeyi ele alacağız.

Sulu nemlendirme daha önceki bahislerde de bahsedildiği gibi hava yıkayıcı püskürtücülerle veya dolgu tipi (matt type) nemlendiricilerle yapılabilir. Bu iki uygulamanın psikrometrik prosesler açısından birbirinden farkı yoktur.

Su ile nemlendirmedeki en önemli özellik havanın içine pulverize su püskürtüldüğü taktirde mutlak nem oranının artmasına ilaveten adyabatik soğutmanın meydana gelmesidir. Isıtılmış havanın nemlendirme işlemi sonucu soğuması, havanın tekrar ısıtılmasını gerekli kılmaktadır. Bu da genelde ikinci bir ısıtıcı batarya gereksinimini ortaya çıkarmaktadır. Bu prosesi belirlerken en doğru yaklaşım oda şartları olan “RA” konumundan işe başlamak olacaktır. Son ısıtıcıda “SA” noktasına kadar ısıtma ve bilahare ısı kaybı nedeniyle mahalde soğuma oda şartları olan “RA” konumundan geçeceği için ilk yapacağımız işlem “RA”dan geçen bir doğru çizmektir. Bu doğru üzerinde “SA” noktasını mahal ısı kayıpları belirler. “2” konumu ise hava yıkayıcı ve nemlendiricinin verimi ile ilgilidir ve proje mühendisi tarafından belirlenir. Konu 5.5.1’de hava yıkayıcı ve nemlendiricilerin verimlerinin %70 ile %95 arsında olduğu belirtilmektedir. Bu nedenle verimi %85 almak doğru bir yaklaşım olur.

“2” noktasını bulduktan sonra bu noktaya ait sabit entalpi çizgisinin “OA” konumundan gelen yatay hat ile kesiştiği “1” noktası da hava yıkayıcı ve nemlendiriciye giriş şartlarıdır.

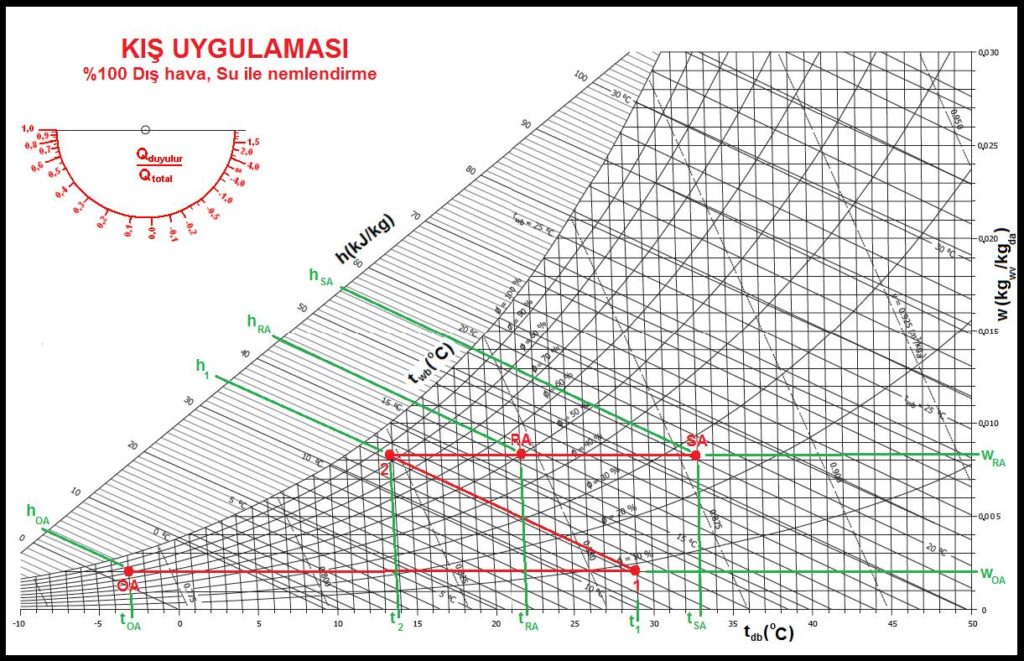
Bu psikrometrik diyagramda görülen OA-1 hattı dış havanın nemlendirmeye uygun koşula kadar ısıtılmasını içermektedir. 2-SA hattı ise adyabatik soğumaya tabi tutulmuş havanın Sa koşuluna kadar ısıtılmasını kapsamaktadır. Bu işlem içinde 2-RA arası havanın mahal şartına kadar ısıtılmasını, RA-SA arası ise mahal ısı kaybını karşılamak için daha da ısıtılmasını içermektedir. Bu prosesleri şu şekilde formülize edebiliriz.

Q_ÖI= V.(1/ɤ)c_p(t₁-t_OA)= V.(1/ɤ)(h₁-h_OA)…………Ön ısıtıcı
Q_SI= V.(1/ɤ)c_p(t_SA-t₂)= V.(1/ɤ)(h_SA-h₂)…………..Son ısıtıcı

Mahal ısı kaybı ise aşağıdaki gibidir.

Q_SI= V.(1/ɤ)c_p(t_SA-t_RA)= V.(1/ɤ)(h_SA-h_RA)………..Mahal ısı kaybı

Bu uygulamaya uygun bir klima santralı örneği aşağıda görülmektedir.

Bu uygulamayı, mahallin taze hava ihtiyacını dikkate alarak %100 dış havalı bir sistem yerine karışım havalı bir sistem olarak ta tasarlamak mümkündür. Psikrometrik diyagramdaki fark OA-RA karışımının ilavesinden ibaret olacaktır. Ancak karışım nedeniyle ısı yüklerinde, özellikle ön ısıtıcı yükünde önemli bir azalma meydana gelecektir.  Karışım havalı uygulamanın psikrometrik diyagramı ve santral şematik çizimi aşağıda yer almaktadır.

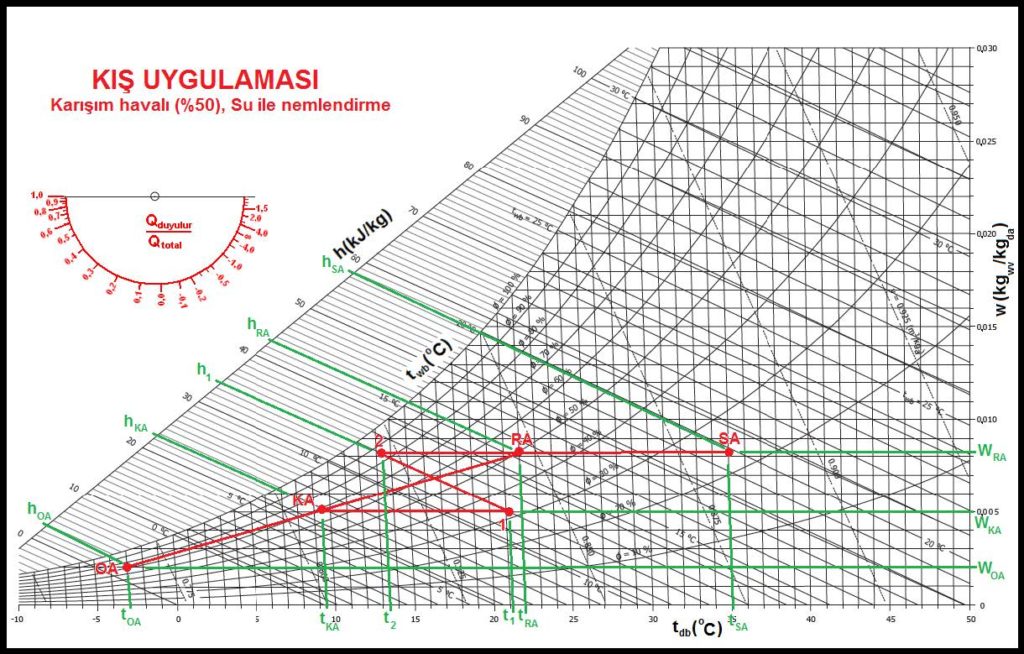
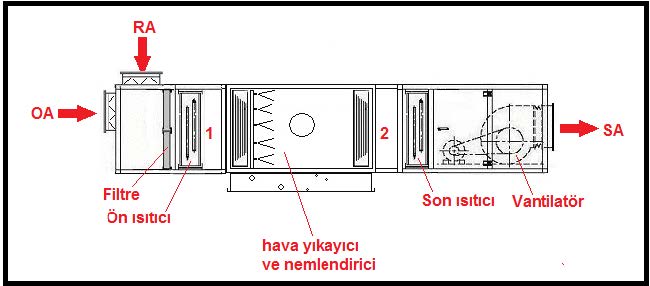
%100 dış havalı uygulama ile karşılaştırdığımızda hava karışımı neticesi ön ısıtıcının kapasitesinin önemli ölçüde azaldığını, ancak son ısıtıcı kapasitesinin değişmediğini görürüz. Havayı nemlendirmek için gereken su miktarında da %50 tasarruf sağlandığı görülmektedir.

6.3. KIŞ UYGULAMASI İÇİN HAVA DEBİSİ VE ISITMA YÜKLERİNİN TESPİTİ-2,

      BUHAR İLE NEMLENDİRMELİ ÖRNEKLER.

 Hava yıkayıcılı nemlendiricilerde bağıl nem oranının oransal kontrolu oldukça zordur. Bu nedenle bu proseslerde iki konumlu uygulamalar genellikle tercih edilmektedir. Çünkü nemlendirme proses hattı üzerinde “2” noktasını herhangi bir yerde sabitlemek ve kontrol altında tutmak oldukça zordur. Bu işlem yalnızca havaya püskürtülen suyun debisinin kontrolu ile yapılamaz. Pulverizasyon, damlacık tanelerinin büyüklükleri ve nozullardaki basınç bunu etkileyen unsurlardır. Bu nedenle sulu nemlendiricilerde elde edilebilecek maksimum verimle ulaşılabilecek “2” noktası hedeflenir ve bu noktanın kontrolu iki konumlu kontrol, örneğin santrifuj pompaya verilen “dur-kalk” komutu ile gerçekleştirilir. Aksi mümkün olsaydı “2” noktası ile “SA” noktası çakıştılmak suretiyle sistem basitleştirilebilir, son ısıtıcı elimine edilebilirdi.

Sulu nemlendiricilerin diğer bir handikapı havada adyabatik soğutmaya neden olmalarıdır. Bu nedenle son ısıtıların kullanımı gerekmektedir.

Üçüncü bir husus ta havaya püskürtülen pulverize suyun buharlaşması ve havaya karışması için belirli bir hacım ve hücre uzunluğuna ihtiyaç göstermeleridir. Bu uzunluk imalatçı firmalar arasında farklılık göstermekle birlikte 1500mm ile 2500mm arasında olduğunu söyleyebiliriz. Bu da klima santralının boyunu uzatmakta, daha büyük makina dairelerine gereksinim göstermektedir.

Buharlı nemlendiriciler bu handikapları gidermek üzere geliştirilmişlerdir. Buharlı nemlendiricilerin sağladıkları faydaları aşağıdaki gibi özetleyebiliriz.

• Oransal olarak kontrol edilmeleri mümkündür. Havaya püskürtülen buhar miktarının oransal kontrolu ile bu işlem kolaylıkla gerçekleştirilmektedir.
• Sulu nemlendiricilerde olduğu gibi uzun hücrelere gereksinim göstermezler, çok daha küçük hacimlerde çözülebilirler. Kanala monte edilebilirler.
• Eğer uygulanan mahalde buhar, örneğin atık buhar mevcutsa enerji açısından son derece ekonomik çözüm getirirler.

%100 haricihavalı , buharlı nemlendiricili bir klima santralının psikrometrik diyagramı ile santralın şematik çizimi aşağıdadır.

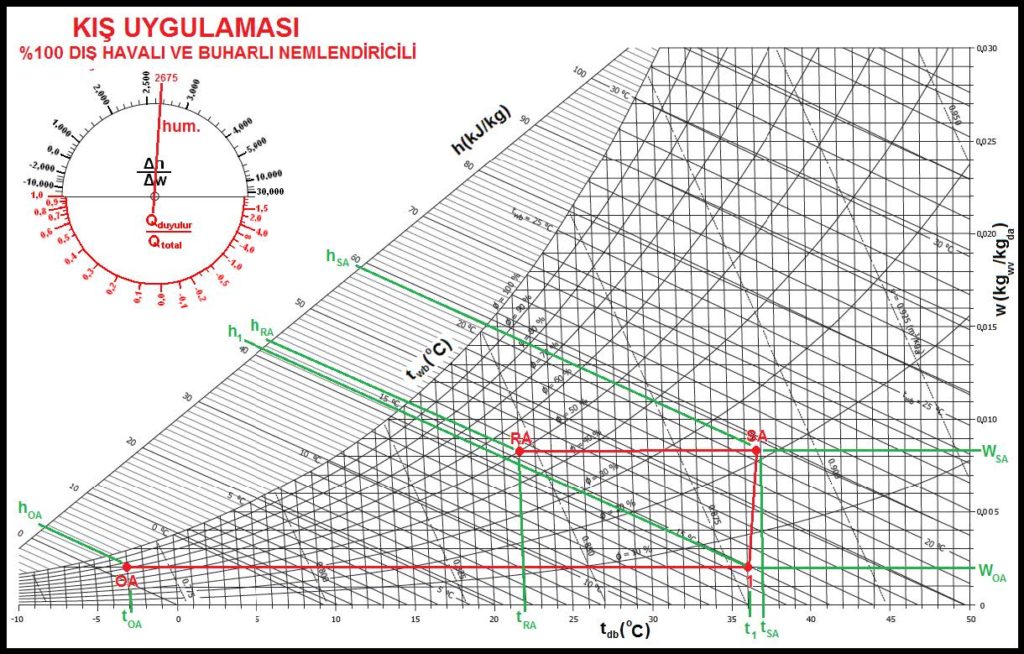
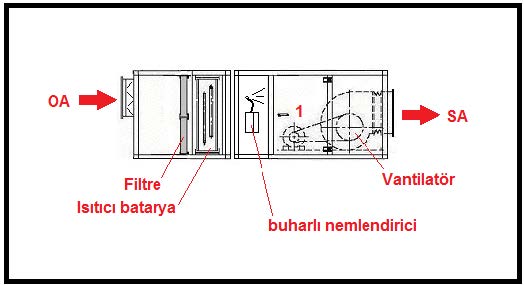
Diyagramda da görüldüğü gibi OA-1 hattı dış havanın ısıtıcı bataryada ısıtılması işlemidir. 1-SA hattı ise buhar püskürtülmesi suretiyle mutlak nem oranının arttırılmasıdır. Konu 5.5.2’de buhar ile nemlendirme bahsi detaylı bir biçimde anlatılmıştır. Örneğimizde elektrodlu buhar jeneratörü kullanıldığı ve doymuş kuru buharın sıcaklığının 100^oC olduğu kabul edilmiştir.100^oC’taki doymuş kuru  özgül entalpisi 2675,57 kJ/kg’dır (Bkz. Tablo-1, Doymuş Haldeki Suyun termodinamik Özellikleri). Bu durumu psikrometrik diyagramın sol üst köşesindeki “Δh/ΔW” skalasına çizer ve bu çizgiyi paralel olarak “1” noktasına taşırız. Bu bizim nemlendirme prosesimizdir.

“SA” noktasında mahalle sevk olunan klimatize hava mahallin ısı kaybı nedeniyle “RA” şartına kadar soğuyacaktır. Bu prosesteki ısıtma ve nemlendirme işlemleri aşağıdaki gibidir.

Q_Isıt= V.(1/ɤ)c_p(t₁-t_OA)= V.(1/ɤ)(h₁-h_OA)………… ısıtıcı

W_nem= V.(1/ɤ)(W_RA-W_OA)= …………………………..…nemlendirici

Bu miktar ön ısıtıcıdan çıkan havaya ilave edilen su buharı miktarıdır ve birimi “kg”dır. Bu işlem için gerekli enerji ise aşağıdaki gibidir.

Q_nem= V.(1/ɤ)(W_RA-W_OA)h_fg= V.(1/ɤ)(h_SA-h₁)….nemlendirici yükü

Bu işlemde “h_fg” birim ağırlıktaki suyun buharlaşması için gerekli entalpidir. (100^oC su için h_fg=2256,47 kJ/kg).

Aynı uygulamayı karışım havalı bir klima santralı ile yaparsak psikrometrik diyagramımız ve klima santralımız aşağıdaki gibi oluşur.

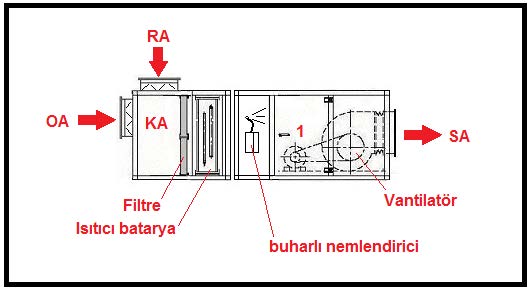
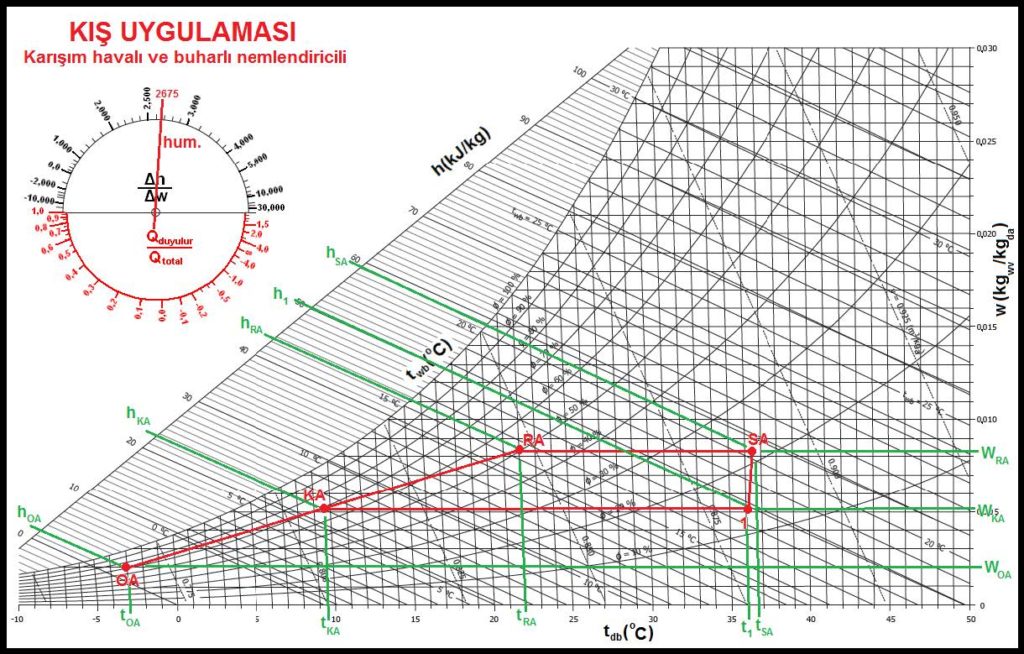
Bu uygulamanın psikrometrik işlemleri bir önceki %100 dış havalı buharlı nemlendiricili klima santralının aynıdır. Aynı formüller kullanılabilir.

6.4. ISI GERİ KAZANIMI

6.4.1 Genel 

Reküperatör kullanılan ısı geri kazanım işlemlerini dört ana grupta toplayabiliriz.

• Çift Serpantinli Isı Geri Kazanım Sistemleri
• Isı Borulu Isı Geri Kazanım Sistemleri
• Plakalı Eşanjörlü Isı Geri Kazanım İşlemleri
• Döner Tamburlu Isı Geri Kazanım İşlemleri

Klima santralarının tasarımı açısından her dört uygulama birbirinden farklılık gösterse de psikrometrik açıdan birbirinin aynıdır. Temel ayırım ısı geri kazanım ünitelerinin ısı geri kazanım tarzlarındaki farklılıktır. Bu açıdan ısı geri kazanım ekipmanlarını iki kategoride toplayabiliriz.

• Yalnız duyulur ısı bazında ısı geri kazanımı gerçekleştirenler
• Entalpi bazında (toplam enerji) bazında ısı geri kazanımı gerçekleştirenler

Diğer bir sınıflandırma da ısı transfer tarzına göredir.

• Direkt ısı transferi ile geri kazanım sağlayanlar
• Üçüncü bir transfer elemanı (hidronik) kullananlar.

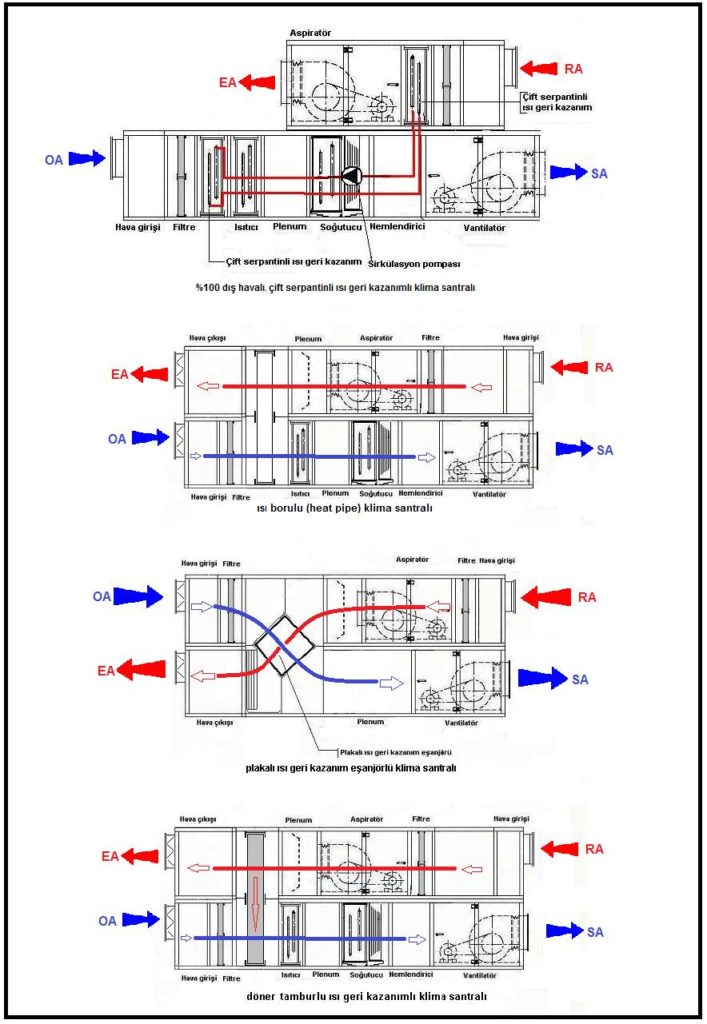
Yukarıdaki şematik çizimde her dört tip ısı geri kazanım uygulaması görülmektedir.

Çift serpantinli ısı geri kazanım sistemleri ile ısı borusu geri kazanım sistemleri ısı transferi için hidronik eleman kullanırlar. Bu eleman çift serpantinli sistemlerde su veya su-etilen glikol karışımıdır. Verimi düşük olan (%40 civarı) ve salt duyulur ısı bazında ısı geri kazanımı sağlayan bu sistemin en büyük avantajı vantilasyon ve aspirasyon ünitelerinin aynı mahalde bulunmaları mecburiyetinin olmamasıdır. Örneğin egzost ünitesi çatıda, klima santralı ise bodrum katta olabilir. Transfer boru donanımı ve sirkülasyon pompası vasıtasıyla gerçekleştirilir.

Isı borusunda ise direkt genleşmeye müsait soğutucu akışkandır; en geniş kullanımı olan R-134’dür. Pomapaya gerek göstermeyen, soğutucu akışkanın dansitesinde buharlaşmaya bağlı olarak meydana gelen değişiklikler nedeni sirkülasyonu kendi içinde sağlar. Verim olarak çift serpantinli sistemlere benzerlik gösterirler.

Plakalı eşanjörlerde metal veya LiBr solüsyonu emdirilmiş selülozik elemanlar egzozt ve dış hava arasındaki bölmeyi oluşturur, bu bölme üzerinden ısı iletimi sağlanır. Bu nedenle plakalı ısı geri kazanım eşanjörleri kararlı rejim çalışması olarak kabul edilirler. Plakaları aluminyum veya benzeri metallerden oluşan eşanjörler salt duyulur ısı transferi yapar ve (^oC) bazında ısı geri kazanımı sağlar. Selüloz, örneğin LiBr veya benzeri sıvı emdirilmiş kağıt  elemanları olanlar duyulur ve gizli ısı transferi yaparlar. Bu eşanjörlere entalpi bazlı ısı geri kazanım eşanjörleri tabir edilir. Plakalı eşanjörlerin verimleri tasarımına bağlı olarak %40 ila %85 arası değişmektedir. Bir plakalı eşanjör aşağıda görülmektedir.

Döner tamburlu eşanjörler salt metal veya satıh kaplamalı metal dolgu malzemesine sahiptirler. Bulundukları klima santralları içinde 80 ila 100 d/dak hızla dönerler. Dönme işlemi küçük bir elektrik motoru vasıtasıyla gerçekleştirilir. Egzost havası tarafındaki tekerleğin yarısı egzost havasının sıcaklığı nedeniyle ısınır ve dönme hareketi neticesi bu havayı soğuk olan dış havaya taşır (yaz aylarında bu işlemin tersi olur). Bu nedenle döner tamburlu ısı geri kazanım eşanjörlerinin çalışma tarzı kararsız rejim olarak kabul edilir. Döner tamburlu eşanjörler üç değişik şekilde imal edilmektedirler:

1. Salt metal (aluminyum) dolgu malzemeli olanlar : Bu modeller yalnız duyulur ısı tarnsferinde kullanılırlar. Dönme işlemi neticesi cüzi bir miktar nemli havayı da sürükleseler gizli ısı transferi açısından bu husus kabili ihmaldir. Oldukça yüksek duyulur ısı geri kazancı verimine sahiptirler ((%70 ve üzeri).
2. Satıhları oksitlenmiş aluminyum dolgu malzemeli olanlar:Bu modellere antalpi tekerleği de tabir edilir. Aluminyum dolgu malzemeleri özel banyolarda oksitlendirilip belirli bir mikron kalınlığında oksit tabakasına sahip olurlar. Bu eşanjörlerin yüksek duyulur ısı geri kazanım verimlerine (%70 ve üzeri) karşılık gizli ısı geri kazanım verimleri oldukça düşüktür (%40 civarı).
3. Dolgu malzemesinin satıhları silika jel kaplı olanlar:Bu modellere absorbsiyon tekerleği de denir. Aluminyum dolgu malzemelerinin sathı özel işlemlerle pulverize silika jel ile kaplanmıştır. Yüksek duyulur ve gizli ısı geri kazanım verimlerine sahiptirler (%70 ve üzeri).

  

6.4.1. Duyulur Isı Bazında Isı Geri Kazanım:

Duyulur ısı bazında ısı geri kazanım işleminde dış hava ile oda havasının mutlak nem oranları eşnjördeki proses nedeniyle değişmemekte, aynı kalmaktadır. Bu proseste, ısı alış-verişi sonucu oluşan sıcaklıkların nasıl hesaplanacağı  TS EN 308’de belirtilmiştir.

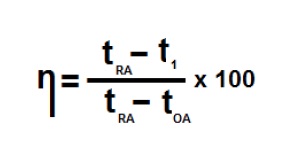
Bu formülde:

η= Eşanjör ısı kazanım verimi ………………………………..…. (%)
t_RA=Egzost edilen havanın sıcaklığı ……………………………. (^oC)
t_OA=Dış havanın sıcaklığı ………………………………………..…. (^oC)
t₁=Egzost edilen havanın eşanjörden çıkış sıcaklığı ……. (^oC)

Bu işlemi psikrometrik diyagramda şu şekilde gösterebiliriz:

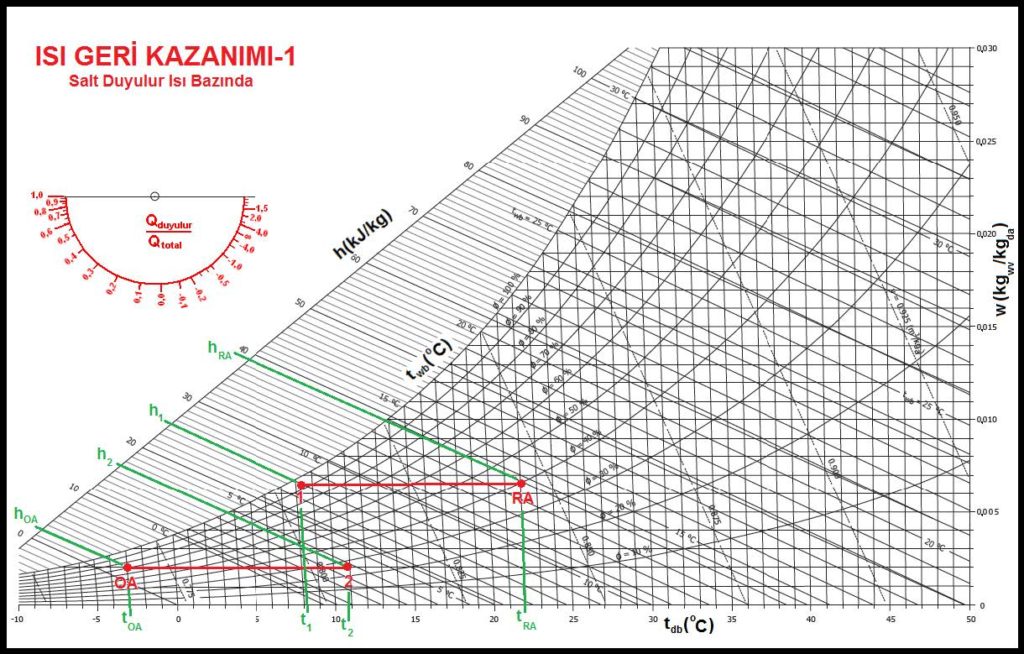
Bu prosesle ilgili olarak şu denklemleri kurabiliriz:

 Q₁=Q₂
Q₁= V(1/ɤ)C_p(t_RA-t₁)= V(1/ɤ)(h_RA-h₁)
Q₂= V(1/ɤ)C_p(t₂-t_OA)= V(1/ɤ)(h₂-h_OA)

Bu denklemlerde egzost ve dış hava debilerinin eşit olduğu varsayılmıştır. Debilerin farklı olması durumunda aynı denklemler “V” değerlerinin eşit olmayan değerlerle değiştirilmesi sonucu elde edilir.

Yukarıdaki örnekte ısı geri kazanım veriminin %55 alınması nedeniyle soğuyan oda havasının oda doyma noktası olan “DP”ye varmadığı görülmektedir. Eğer verim daha yüksek olsaydı ve bunun neticesi hesaplanan “t₁” sıcakığı doyma eğrisinin dışında çıksaydı bu durumda entalpi eşitlikleri ile prosesi belirlemek gerekecekti. Bu durumu verimi %80 olan bir ısı geri kazanım eşanjörü ile gösterelim.

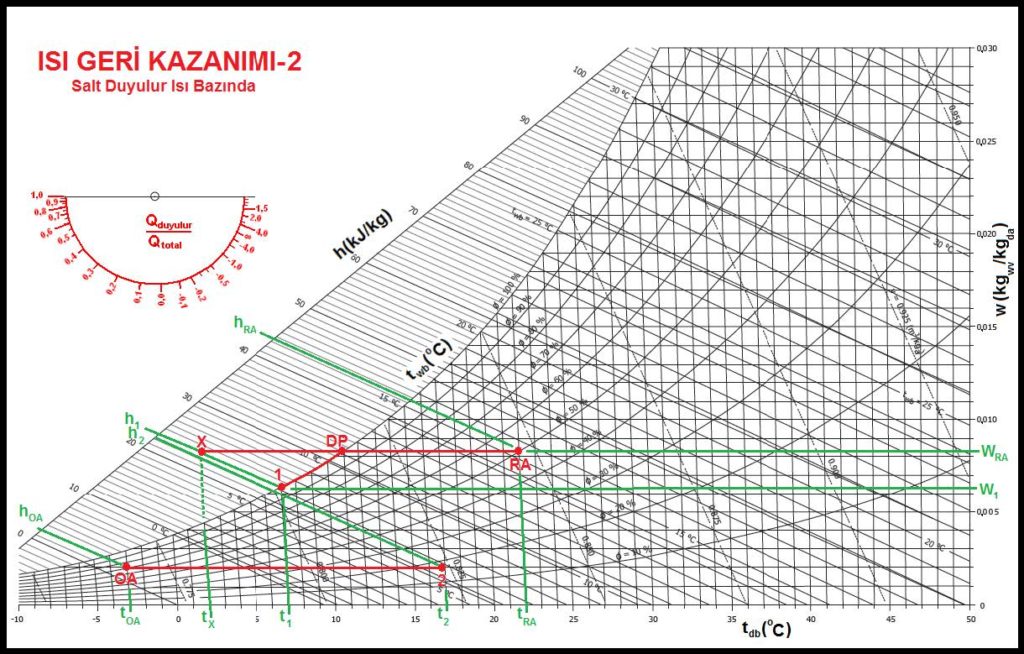 Bir önceki sayfada vermiş olduğumuz verim denklemini %80 için yaptığımızda hayali “t_x” noktasını +2^oC olarak buluruz. Ancak bu sıcaklık doyma eğrisinin üstünde olduğu için mümkün değildir. Ancak bu sıcakılığın özgül entalpisi denklemde kullanılabilir.

Q₁=Q₂
Q₁= = V(1/ɤ)(h_RA-h₁)        ( h_x=h₁)
Q₂= V(1/ɤ)C_p(t₂-t_OA)= V(1/ɤ)(h₂-h_OA)

Bu işlemde egzost edilen hava “DP” sıcaklığından daha düşük bir sıcaklığa soğutulduğu için yoğuşma meydana gelmektedir. Eğer “1” noktası 0^oC’ın altında olsaydı bu sefer karlanma ve buzlanma yoğuşmanın yerini alacaktı.

Yoğuşma ve karlanma olan plakalı ısı geri kazanım eşanjörlerinin egzost tarafında bir yoğuşma kabı bulunması gereklidir. Eğer karlanma olayı varsa defrost tertibatı bulunmalıdır. Bu husus konumuz dışı olduğundan detayına girilmeyecektir; imalatçı firmalarla temasa geçilmesi tavsiye olunur.

6.4.2. Toplam Isı (Entalpi) Bazında Geri Kazanım:

 Toplam ısı bazında ısı geri kazanımı hem duyulur ısı bazında “^oC” olarak, hem de gizli ısı bazında “W” olarak ısı geri kazanımını, diğer bir ifadeyle hem ısı hem de kitle transferini içermektedir. Bu nedenle iki değişik verim değerinin belirtilmesinde yarar vardır. Bunlardan biri duyulur ısı geri kazanım verimi, diğeri de gizli ısı geri kazanım verimidir.

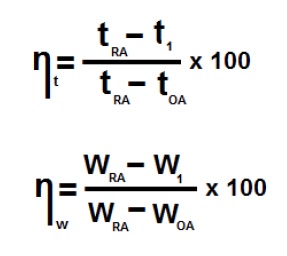
Bu işlemi psikrometrik diyagrama aktarabilmemiz için “t₁” ve “t₂” değerlerine ilaveten “W₁” ve “W2” değerlerini de bulmamız gerekmektedir. Burada yapacağımız işlemi şu şekilde özetliyebiliriz:

1. Duyulur ısı bazında ısı geri kazanımı verimi “η_t“yi esas alarak “t₁” egzost havası eşanjör çıkış sıcaklığını belirleyin. Bu noktanın kuru termometre koordinatından sabit kuru termometre çizgisini çizin (diyagramda “t₁” noktasından yukarı doğru uzanan yeşil çizgi).
2. Isı denklemini kurup dış havanın eşanjörden ısınmış olarak çıkacağı “t₂” noktasını belirleyin. Bu noktanın kuru termometre koordinatından da aynı şekilde sabit kuru termometre çizgisini çizin (diyagramda “t₁” noktasından yukarı doğru uzanan yeşil çizgi).
3. Psikrometrik diyagramdan “W_RA” ve “W_OA” değerlerini bulun.
4. “η_w“ verim değerini esas alarak diyagramdan “W₁” ve “W₂” değerlerini hesaplayın. Her iki değer için mutlak nem oranı ordinatına dik iki sabit mutlak nem çizgisini çizin (Bizim örneğimizde verim %50 olduğu için her iki hat üst üste çakışacaktır).
5. “W₁” yatay hattı ile “t₁” dikmesinin kesiştiği nokta “1” konumudur.
6. “W₂” yatay hattı ile “t₂” dikmesinin kesiştiği nokta “2” konumudur.
7. RA-1hattı eşanjörde egzost havasının soğuma hattıdır. Aynı şekilde OA-2 hattı da ısı geri kazanımı ile dış havanın ısınma ve nem kazanma hattıdır.

Aşağıdaki psikrometrik diyagramda mahal şartları 22^oC, %50 rH, dış hava şartları -3^oC, %30 rH  ve eşanjör verimleri η_t=%75, η_w=%50 olan bir uygulama örneği verilmektedir.

  

6.5. ISI GERİ KAZANIMLI KLİMA SANTRALI ÖRNEKLERİ

6.5.1.  Kış Uygulaması

Kış kliması örneğimizde antalpi bazlı ısı geri kazanım tamburu olan, karışım havalı ve buharlı nemlendiricili bir klima santralını inceleyeceğiz.

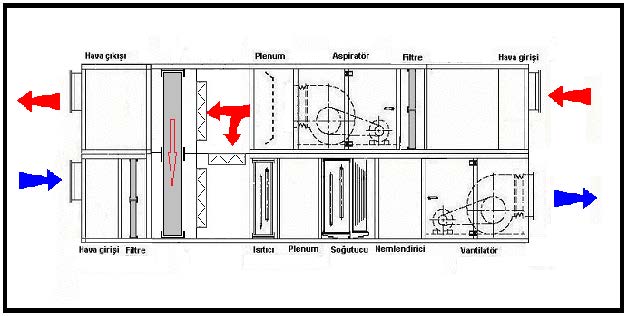
Klima santralımız dört mevsim çalışmak üzere dizayn edildiği için bünyesinde soğutucu batarya da bulundurmaktadır. Önce kış klima uygulamasını inceleyeceğiz, bilahare yaz klimasını göreceğiz.

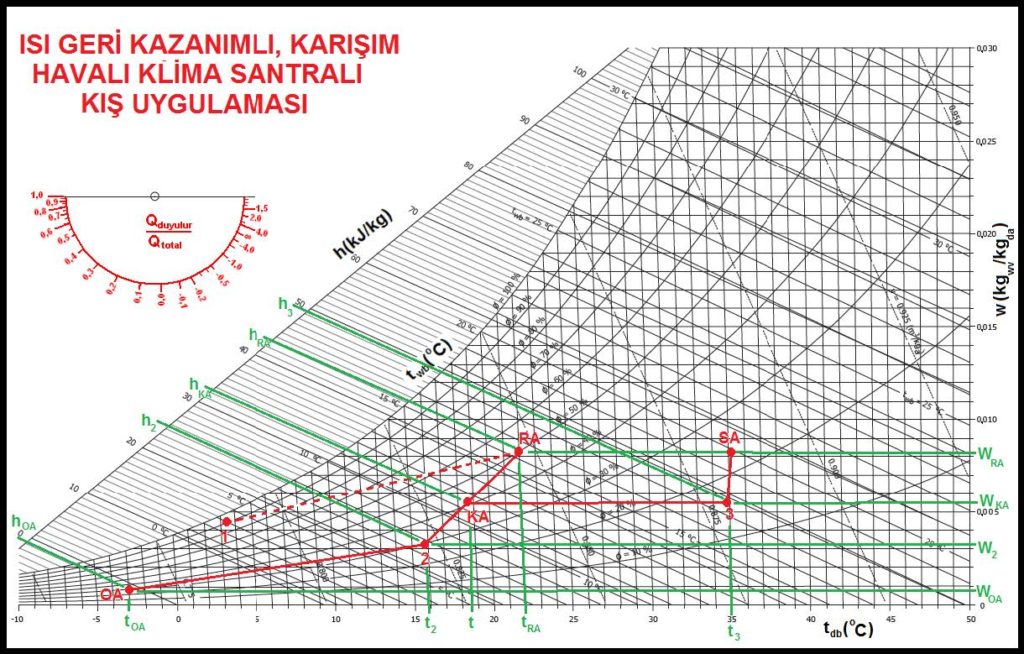
Isı geri kazanım işlemi 6.4.3’deki örneğin aynıdır. Ancak egzost ettğimiz hava psikrometrik proses açısından bizi ilgilendirmediğinden kesin çizgilerle gösterilmiştir. OA-2 dış havanın döner tamburlu ısı geri kazanım cihazında ısı ve mutlak nem kazanmasını göstermektedir. “2” konumundaki hava, döner tamburlu eşanjörden geçmeyen %50 oranındaki mahal havası ile karışmaktadır. Bu proses 2-RA hattı olup karışım noktası “KA” ile gösterilmiştir. KA-3 hattı ise ısıtıcı bataryada karışım havasının ısıtılması hattıdır. “3” noktasındaki havanın beher kligramına “W_ra-W_ka” kadar buhar ilavesi ile nemlendirme yapılmaktadır. “SA” noktası ise klimatize havanın mahalle sevk olunduğu konumdur.

Bu uygulamada entalpi bazlı ısı geri kazanım tamburunun kullanımının getirdiği avantajlar açıkça görülmektedir. Örneğin KA-3 ısıtma proses çizgisi kısalmıştır. Eğer ısı geri kazanımı olmasaydı karışım işlemi OA-RA hattı üzerinde yapılacak ve ısıtma bataryası da bunun neticesi olarak daha büyük çıkacaktı. Keza aynı mantığı nemlendirme prosesi için de yürütmek mümkündür. “KA” noktasının daha solda ve aşağıda bir konumda olması gerekli buhar miktarında da artışa neden olacak, neticede daha büyük bir buharlı nemlendirici kullanılacaktı. Bu da bize işletme maliyeti açısından büyük avantajlar sağlamaktadır.

6.5.1. Yaz Uygulaması

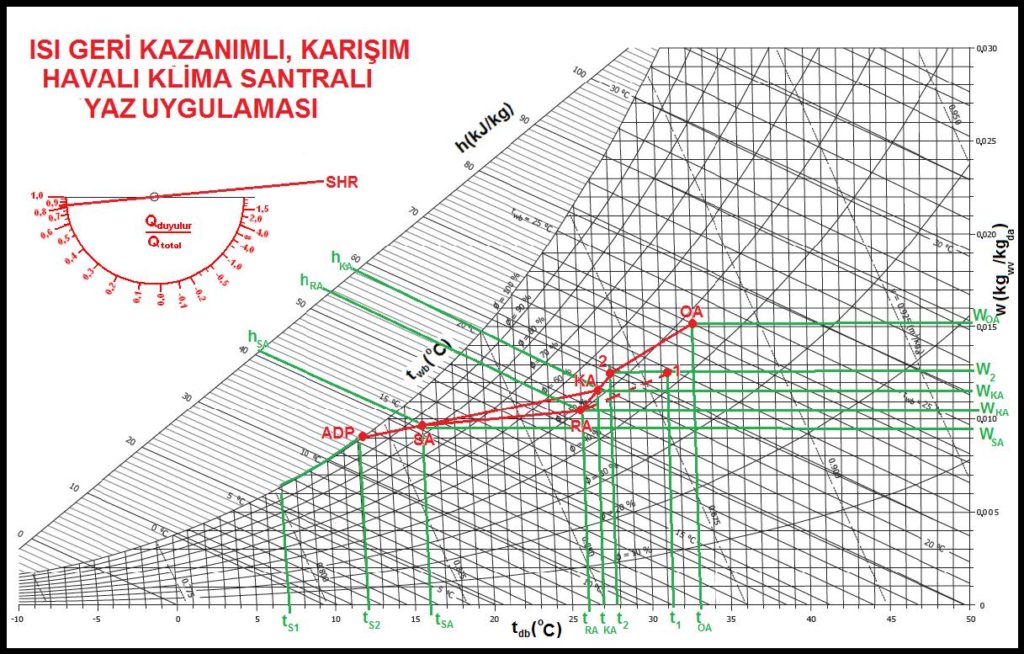  Yukarıdaki psikrometrik diyagramımızda 550 karışım havalı bir yaz uygulaması görülmektedir. Veriler aşağıdaki gibidir.

η_duy= %75……………………  Duyulur ısı verimi

η_giz= %50………………….  Gizli ısı verimi

Dış hava oranı = %50

Oda şartları:

26^oCKT, %50rH,    RSHR=0,82

Bu diyagramda “OA-2” hattı dış havanın döner tamburdan geçerken soğuması ve mutlak neminin belirli bir miktarını bırakmasını, “SA-1” hattı da egzost edilen mahal havasının ısınırken dış havadan transfer edilen nemi bünyesine almasını göstermektedir. Ancak egzost havası bu aşamada bizleri ilgilendirmediği için yalnız malumat kabilinden kesik çizgiler halinde gösterilmiştir. Bir antalpi bazında ısı geri kazanımı aparatından hava çıkış şartlarının hesabı 6.4.3.’de gösterilmiştir.

“2-RA” hattı oda havası ile döner tamburlu ısı geri kazanım cihazından çıkan havanın karışım prosesinin meydana geleceği hattır ve “KA” noktası karışım noktasıdır.

“RA-SA” ESHR’ye eşit olup oda efekti neticesi havanın mahalde ısınması işlemini göstermektedir. Havanın 10^oC sıcaklık farkı ile üfleneceği kabul edildiğinden “KA-SA-ADP” hattı da klima santralı soğutma bataryasındaki soğutma prosesidir. Daha önceki bahislerde anlatıldığı gibi ADP kuru termometre sıcaklığı soğutucu su çıkış sıcaklığına eşit alınırsa, soğutucu bataryada sirküle eden soğutulmuş su 7/12^oC bulunur.

6.6. DEĞİŞKEN HAVA DEBİLİ SİSTEMLER

 Değişken hava debili sistemlerde iki temel uygulama tipi vardır.

1. Yaz ve kış uygulamasında değişken hava
2. Yaz uygulamasında değişken hava, kış uygulamasında miminum debide sabit hava.

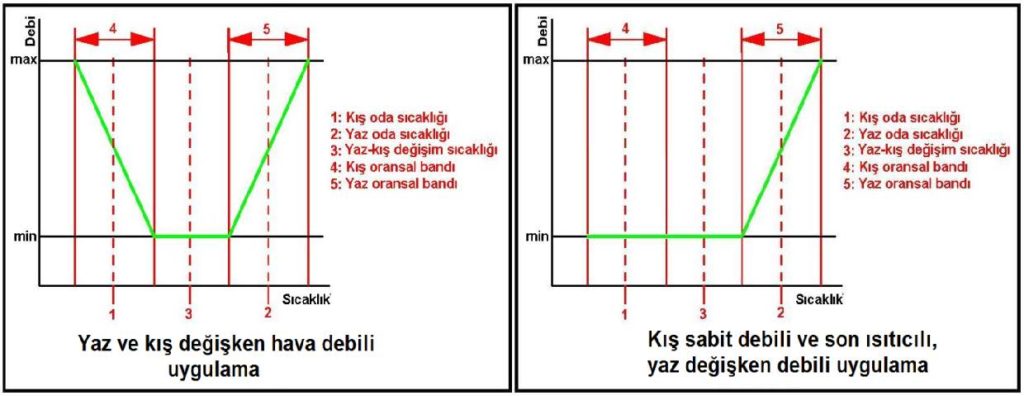
VAV terminal üniteli sistemlerin en büyük özelliklerinden biri mahallin sıcaklığının kontrolunu üflenen havanın sıcaklığını ayarlayarak yapmak yerine sabit sıcaklıkta ve değişken debide hava sevk etmesidir. VAV ismi de buradan kaynaklanmaktadır, “Değişken Hava Debili” tabirinin İngilizcesinin baş harflerinden oluşmaktadır.  Bu sistemde maksimum debi mahallin maksimum yaz yüküne göre, minimum debi de IAQ’ya bağlı olarak mahaldeki insan sayısına göre belirlenir. Mahal sıcaklık değişimine bağlı olarak hava debisi oransal olarak regüle edilir. Bu uygulama yaz-kış uygulanabileceği gibi (Bkz üstteki diyagram sol çizim) enerji ekonomisi açısından yaz uygulamasında değişken hava debisi, kış uygulamasında ise minimumda sabit hava debisi uygulaması da yapılabilir (Bkz. Sağ çizim). Kış çalışmasında minimum debi uygulaması yapılıyorsa klima santralı hava çıkışı miminum sıcaklıkta, örneğin 16^oC’ta sabit tutulur, mahallin bakiye ısı ihtiyacı VAV terminal ünitesinin hava çıkış tarafına yerleştirilen bir ısıtıcı batarya ile gerçekleştirilir.

VAV terminal ünitelerinin diğer bir özelliği de değişen basınç farkları, örneğin giriş basınçları karşısında sabit debi uygulamsını yapabilmesidir. Özellikle HEPA filtreli uygulamalarda faydalanılan bu özellik konumuz dışı olduğundan yalnızca bilgi vermekle yetinilecektir.

Aşağıdaki psikrometrik diyagramda VAV terminal üniteli, değişken hava debili sistemlerin yaz-kış uygulamaları gösterilmektedir.

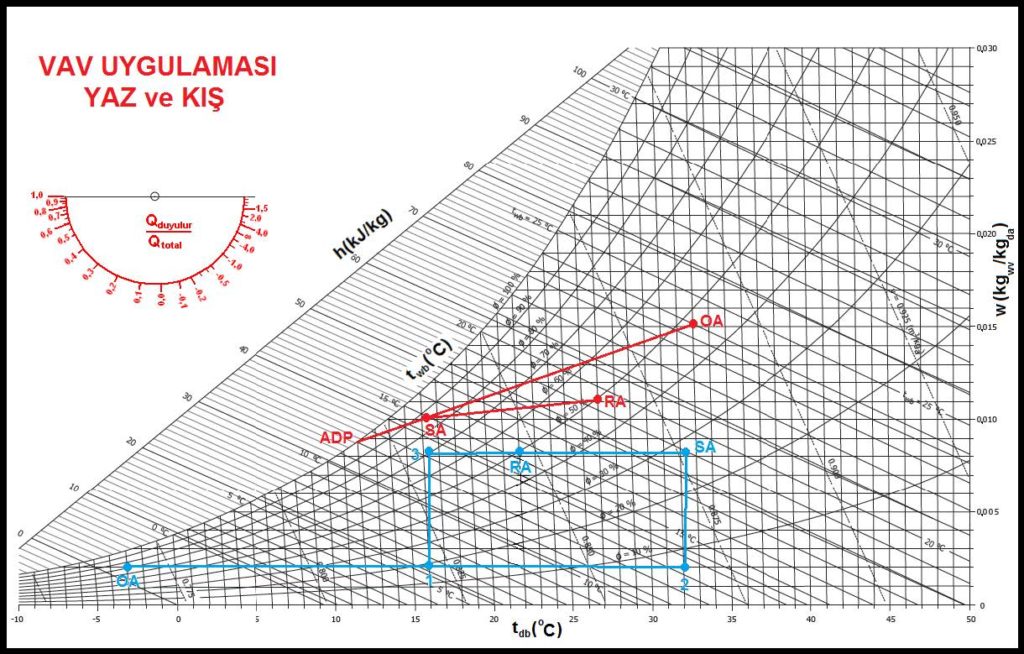
Diyagramda kırmızı çizgiler yaz uygulamasını, mavi çizgiler de kış uygulamalarını göstermektedir. Her iki uygulama için 5100 dış hava kabul edilmiştir. Yaz uygulamasında “OA” şartlarındaki hava klima santralında “SA” şartlarına kadar soğutulmakta ve mahalle sevk olunmaktadır. “SA-RA” hattı mahalde oda efekti neticesi duyulur ve gizli ısı kazancını göstermektedir. Bu uygulamada “SA” konumu daima sabittir. (Dış hava şartlarındaki değişikliklerin bu konum üzerindeki etkisi  tolere edilebilecek sınırlar içindedir). Mahal ihtiyaçlarına bağlı olarak üflenen havanın debisi oransal olarak kontrol edilmekte, azaltılmakta veya çoğaltılmaktadır.

Kış uygulamasında ise iki alternatif mevcuttur.

1. Değişken hava debili uygulama
2. Sabit hava debili ve son ısıtıcılı uygulama

Değişken hava debili uygulamada dış hava klima santralında “OA” konumundan “2” konumuna kadar ısıtılmaktadır. Bilahare buharla nemlendirilen hava “SA konumunda mahalle sevk olunmaktadır. “SA-RA” hattı ise mahalde ısı kaybı neticesi soğumayı göstermektedir. Bu proseste üflenen havanın sıcaklığı sabittir. Mahal ısısı yaz uygulamasında olduğu gibi debinin oransal reglajı ile sağlanmaktadır. Nemlendirici kullanıldığı taktirde bağıl neme bağlı olarak oransal kontrol yapılabilir.

Sabit hava debili kış uygulamasında ise hava belirlenmiş olan minimum debide sabit debili olarak üflenmektedir. Klima santralındaki ısıtma işlemi “OA-2” prosesi olup sıcaklık  sabittir. “2-3” arasında nemlendirme prosesine tabi tutulan hava VAV terminal ünitesindeki son ısıtıcı serpantine girmektedir. Burada hava “3-SA” prosesi ile ısıtılmakta ve mahalle sevk olunmaktadır. Mahal sıcaklığını sabit tutabilmek için, hava debisi sabit olduğundan “SA” üfleme sıcaklığı mahal yüküne bağlı olarak oransal kontrol edilmektedir.

6.7. ENDÜKSİYON SİSTEMLERİ 

Endüksiyon cihazları klima santralında şartlandırılmış primer havanın bir cihaz içindeki nozullardan yüksek hızla üflenmesi, yüksek hız ile yaratılan kısmi vakum sayesinde sekonder hava olarak tabir edeceğimiz mahal havasının cihazdaki serpantin üzerinden endüklenmesi ve soğutulması esasına dayanır. Primer ve sekonder hava cihaz içinde karışıp mahalle sevk olunurlar.

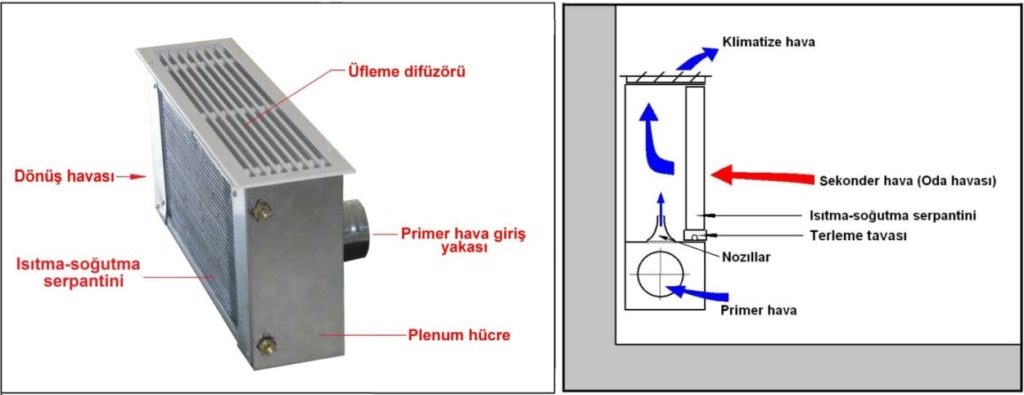
Yukarıdaki resimde bir endüksiyon cihazı ve çalışma prensibi görülmektedir. Endüksiyon cihazının psikrometrik analizine geçmeden önce cihazın çalışma prensibini bilmekte fayda vardır.

Endüksiyon cihazının içinde primer havanın girdiği bir plenum hücre vardır. Bu plenum hücrenin üst tarafında nozıllar bulunmaktadır. Bu nozıllar vasıtasıyla primer hava ısıtma-soğutma serpantinine paralel bir şekilde ve yüksek hızda üflenmektedir. Bu sayede serpantinin arka tarafında kısmi vakum yaratılmakta ve basınç farkı nedeniyle sekonder hava tabir ettiğimiz oda havası serpantin üzerinden cihaz içine emilmekte, diğer bir tabirle endüklenmektedir. Serpantin arkasındaki haznede primer ve sekonder havalar karışmakta, klimatize edilmiş hava olarak mahalle sevk olunmaktadır. Burada iki değişik proses ve bunların neticesi iki değişik hava kütlesinin karışması meydana gelmektedir. Primer hava önceden belirlenmiş şartlarda merkezi klima santralında klimatize edilmekte ve cihaza sevk olunmaktadır. Mahal şartlarındaki sekonder hava ısıtma-soğutma serpantini üzerinden geçerek soğumaktadır. Bu iki hava birbiriyle karışmakta ve mahalle sevk olunmaktadır.

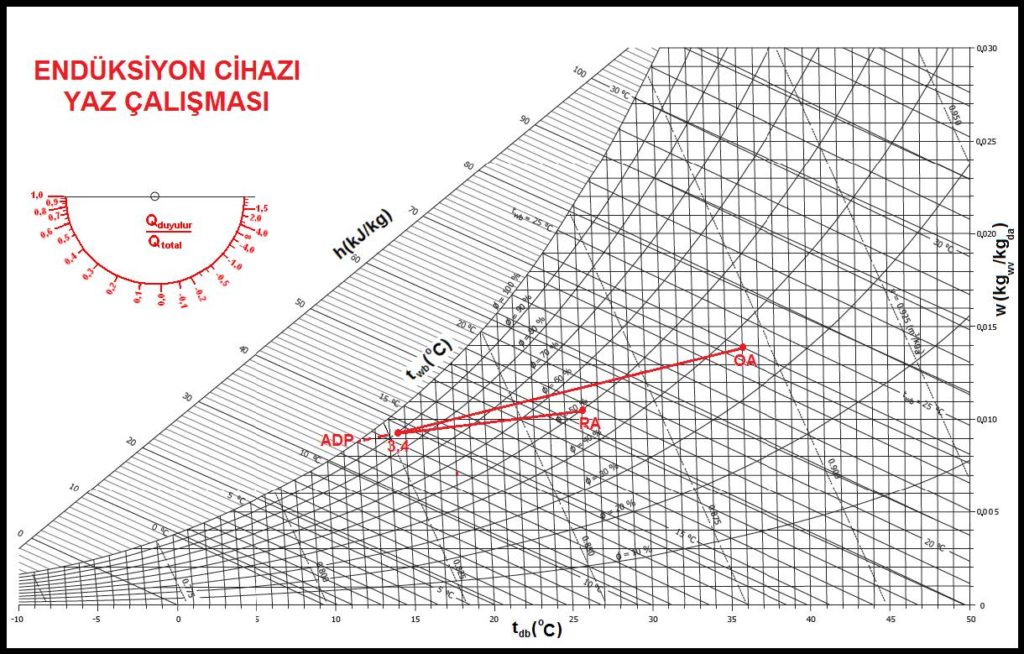
Yukarıdaki proseste iki değişik işlem yer almaktadır. Dış hava klima santralında “3” koşuluna kadar şartlandırılıp primer hava olarak endüksiyon cihazına sevk olunmakta ve nozıllardan püskürtülmektedir. Mahal havası “RA” da “4” şartlarına kadar endüksiyon cihazı içinde şartlandırılmaktadır. Soğutucu olarak her iki sistemde de aynı akışkan kullanıldığından sistemlerin ADP’leri birbirlerine çok yakındır ve bu nedenle “3” ve “4” noktaları çakışmakta aynı zamanda mahalle sevk olunan karışım havası şartlarını oluşturmaktadır. Bu çalışmada “RA”nın mutlak nem oranı “4” şartının  nem oranından fazla olduğu için endüklenen havayı soğutan serpantin üzerinde kondansasyon meydana gelmektedir. Bu kondansasyon serpantin altındaki terleme tavasınca toplanıp drene edilmektedir.

Benzeri bir uygulama da endüksiyon ünitesindeki soğutma serpantini üzerinde yoğuşma olmaksızın, mahal havası “RA”yı yalnız duyulur olarak soğutmaktır. Bu işlem aşağıdaki psikrometrik diyagramda gösterilmektedir.

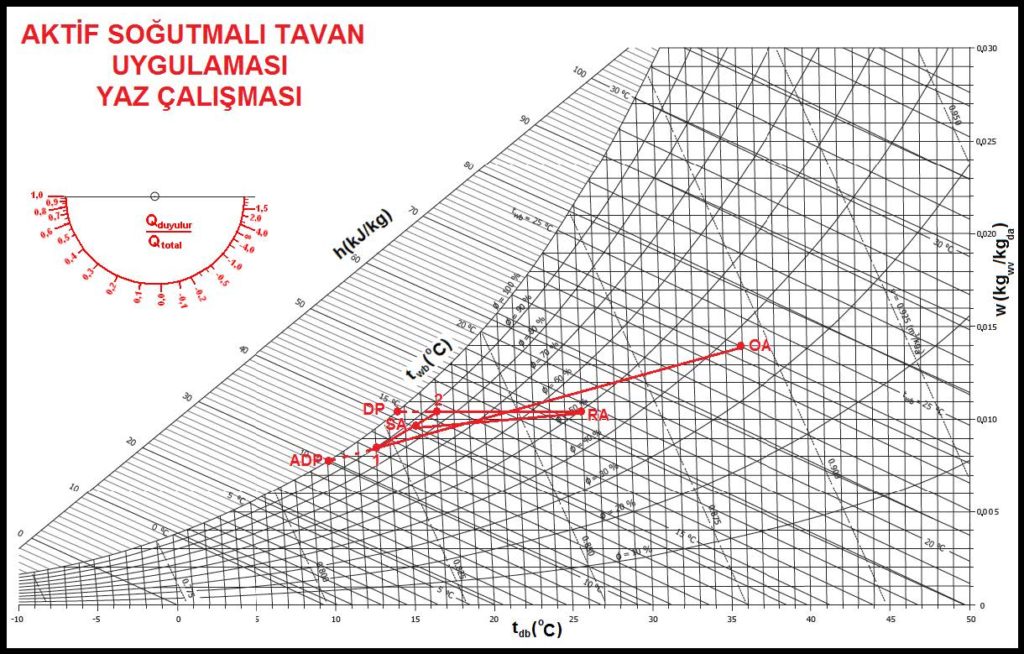
Bu tarzda çalışan cihazlara “aktif soğutmalı tavan” veya “aktif soğutmalı ünite” tabir edilmektedir. Endüksiyon cihazlarına çok benzeyen bu ünitelerin içinde drenaj tertibatı yoktur. Bu cihazdaki işlemi psikrometrik açıdan şu şekilde izah edebiliriz.

“OA” şartlarındaki primer hava “1” şartına kadar soğutulmaktadır. Kullanılan soğutucu akışkan 6/10^oC soğuk su olduğu için “ADP” noktası da 10^oC olarak çıkmaktadır. Endüklenen oda havası (sekonder hava) “2” şartlarına kadar soğutulmaktadır. Bu serpantinde kullanılan su sıcaklık kontrollü olup dönüş sıcaklığı “DP”ye eşit alınmakta, ayrıca serpantin satıh sıcaklığı ölçümü yapılarak soğuk su debisi ve dönüş sıcaklığı kontrol altında tutulmaktadır. Serpnatinden “2” şartlarında çıkan sekonder hava ile nozıllardan üflenen “1” şartlarındaki hava “SA” şartlarında karışmakta ve mahalle üflenmektedir. Bu uygulamanın en büyük özelliği sekonder havada yalnız duyulur soğutma yapılmasına rağmen primer hava sayesinde mahal bağıl nem şartları kontrol altında tutulabilmektedir. Bu uygulamada kullanılan primer-sekonder hava karışım oranları ile elde edilebilecek minimum RSHR imalatçılara bağlı olmakla birlikte yaklaşık olarak miminum RSHR değerinin %80, karışım oranının da 1/3 primer hava 2/3 sekonder hava olduğunu söyleyebiliriz. Hassas değerler için imalatçı firmaların kataloglarına bakılmalıdır.

6.8.1. HAVANIN NEMİNİN ALINMASI

6.8.1.Soğutma İle Nem Alma

Soğutma ile nem alma işlemi nemli havanın  çiy noktası “DP”den daha düşük bir sıcaklığı soğutulmasını ve bilahare mahal şartlarına kadar ısıtılması prosesini içerir. Bilinen en klasik nem alma sistemidir.

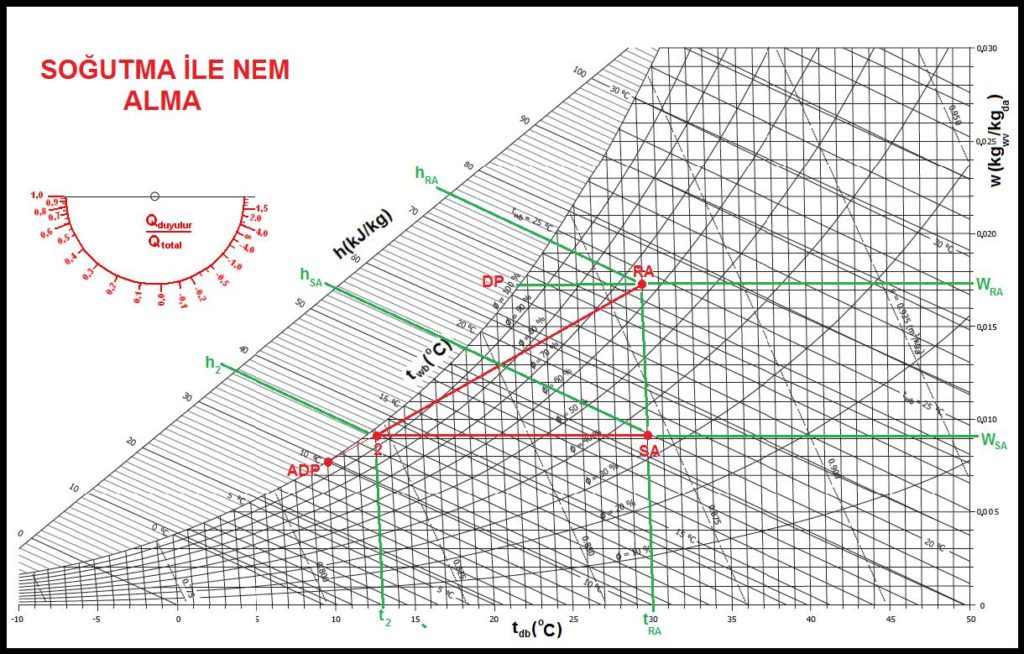
Bu işlemi ve gerekli hava debisinin belirlenmesini şu şekilde ifade edebiliriz.

M_w= Alınması gereken nem miktarı (kg/h)

Mahal şartları “RA” için h_RA, t_RA, w_RA

Seçilen soğutucu akışkan, R407C,

T_evap=+5^oC,

ΔT_superheat=5^oC

Bu verilerle ADP=+10^oC bulunur. Soğutma prosesi eğrimiz “RA-ADP”dir.

By-pass oranını kabulle “2” noktası bulunur.

Hava debisi:

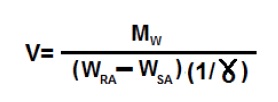
Buradan da gerekli soğutma kapasitesini bulabiliriz.

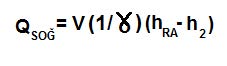
Mahal şartlarına kadar ısıtmak için gerekli olan ısıtma kapasite de:

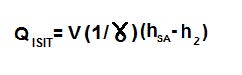
Soğutma ile nem alma sistemlerinde soğutucu batarya üzerinde homojen bir ısı dağılımı gerçekleştireceği için doğrudan genleşmeli sistemler tercih edilmelidir. 

6.8.2. Adsorbsiyonlu Nem Alma Sistemleri

Soğutma ile nem alma uygulamalarında  mutlak nem oranının azaltılması ADP ile sınırlıdır. Teorik olarak ADP’yi daha aşağılara çekmek soğutucu bataryada kullanılan direkt genleşmeli gazın evaporasyon sıcaklığını düşürmek ile mümkün olacak gibi görünse dahi pratikte bu mümkün değildir. Çünkü evaporasyon sıcaklığının aşırı düşürülmesi, örneğin 0^oC’ın altındaki değerlere çekilmesi batarya yüzeylerinde karlanmaya neden olacak, nem alma randımanını düşürecektir. Defrost yapılsa dahi kesintili çalışma olacağı için verimde yine düşmeler olacaktır. Evaporasyon sıcaklığının 0^oC’ın biraz üzerinde, örneğin +2^oC gibi bir seviyede tutulması da bu mahsuru gidermemektedir. Çünkü kısmi kapasite kullanımlarında da evaporasyon sıcaklığı azalacak ve karlanma olayı yine meydana gelecektir. Kademeli kapasite kullanımlı ve frekans konvertörlü kompresörlerle bunun önüne kısmen geçilse dahi 0^oC evaporasyon bu uygulamanın alt limiti olacaktır. 4^oC aşırı ısınma (superheat) sıcaklığı kabul edilse dahi ADP’yi bu derecenin altına çekmek mümkün olmamaktadır. Evaporasyon sıcaklığının düşmesi komprsörlerde kapasite azalmasına da neden olmakta, daha büyük kompresörlerin seçilmesi gerekmektedir.

Bu negatif hususların önüne geçmek için adsorbsiyonlu nem alma sistemleri geliştirilmiştir. Adsorbsiyonun anlamı taşınım yoluyla nem tutmadır. Bu işlem için “dessicant” tabir edilen özel tamburlar kullanılmaktadır. Isı geri kazanım sistemlerinde kullanılan tamburlara son derece benzeyen bu tamburların ana maddesi aluminyum yerine silika-jel’dir. Tamburlar fibrocam dokudan yapılmakta, bu dokunun üstü silika-jel kaplanmaktadır. Silika-jel tamburun %80’ini oluşturmaktadır. Ayrıca üzerinde koruyucu olarak akrilik bir kaplama da bulunmaktadır.

Silika-jel kaplı “Dessicant” tambur  (Pro-flute firması müsaadesiyle)

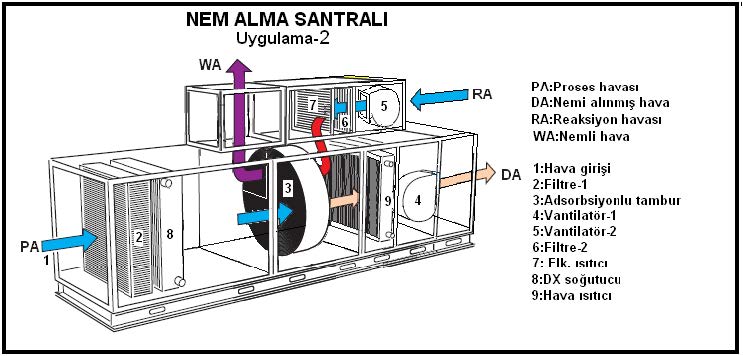
Bu uygulamada genelde tamburun ¾’ü hava kurutmada, 1/4’ü de tamburun adsorbe etmiş olduğu nemin dışarı atılmasında kullanılır.Adsorbsiyonlu nem alma santralı aşağıda şematik olarak gösterilmektedir.

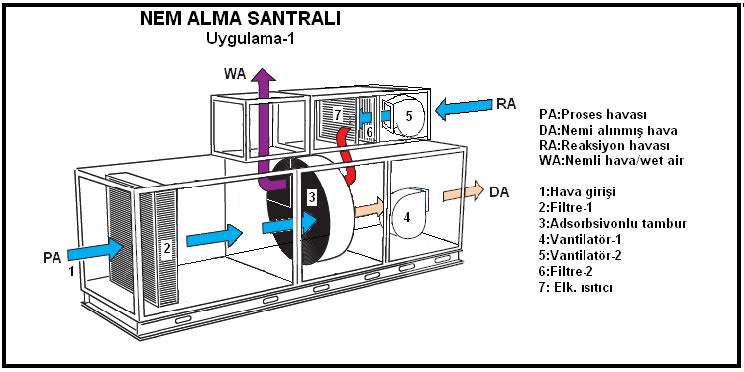
Bu uygulamada “PA” rumuzlu proses havası, nemi azaltılmak istenen mahal havasıdır. “RA” ise yaklaşık 120^oC’a ısıtılmış reaksiyon havası tabir edilen kurutucu havadır. Bu uygulamada döner tambur çok düşük bir devirle dönmektedir (yaklaşık 20 tur/saat). “PA”da bulunan nem 3 numaralı tambur tarafından adsorbe edilmekte ve nemi azalmış hava “DA” 4 numaralı vantilatör tarafından mahalle üflenmektedir. “PA” tamburun ¾’ünden geçmektedir. “RA” filtrelendikten sonra 120^oC’a ısıtılmakta, tamburun bakiye ¼’lük kısmından geçerek tamburun kurutulmasını sağlamaktadır. Tamburun devamlı bir dönme hareketi içinde olması “PA”daki nemin alınmasına ve bu tamburun sıcak “RA” ile teması neticesi kurumasına ve işlemine devam devam etmesine neden olmaktadır. Bu işlem aşağıdaki psikrometrik diyagramda görülmektedir.

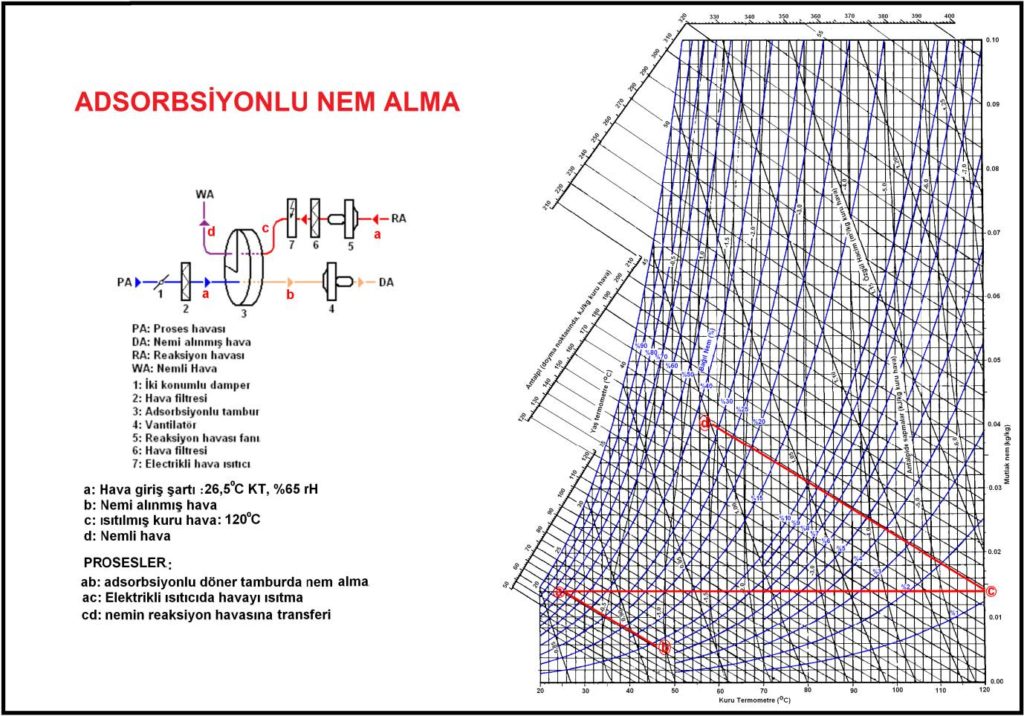
Bu proseste “RA” reaktif hava olarak mahal havası kullanılmakta, bu uygulama ile mahallin havalandırılması da sağlanmaktadır.

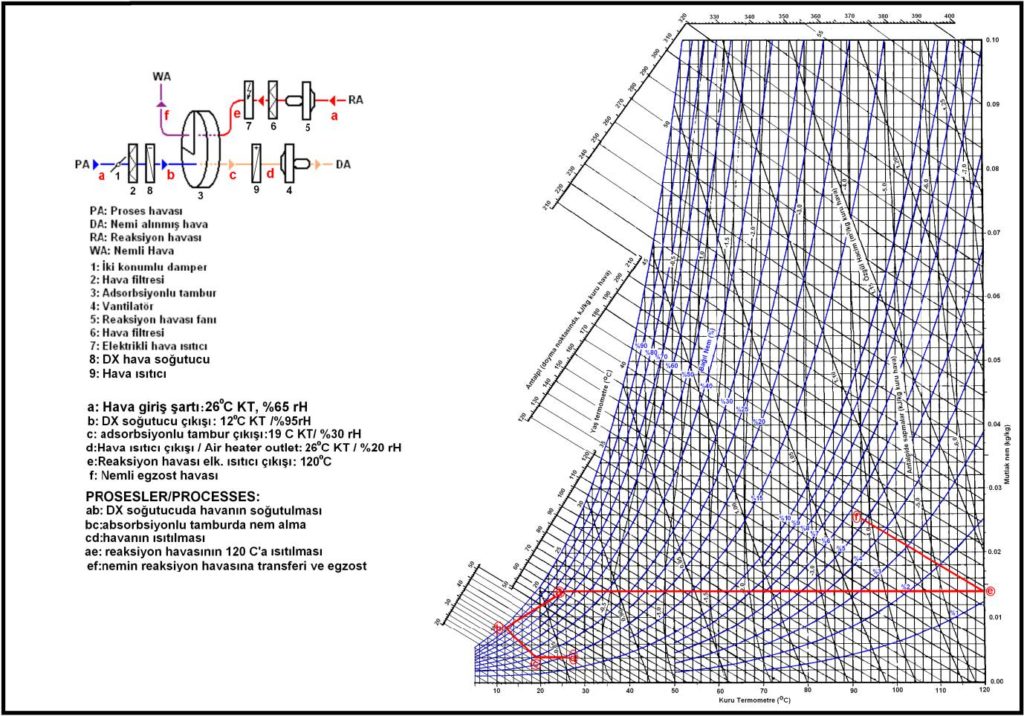
Çok düşük mutlak nem oranı istenen uygulamalarda çift tambur veya mekanik soğutma ile birlikte adsorbsiyonlu nem alma uygulaması da yapılmaktadır. Bu tip bir santralın şematik çizimi ve psikrometrik diyagramı aşağıdadır. Bu işlemde mahal havası “PA” önce soğutulmakta ve bu surette mutlak nem oranı azaltılmaktadır. Bilahare adrosbsiyonlu nem alma tamburundan geçen havanın nemi daha da azaltılmaktadır. Bu prosesler psikrometrik diyagramda ab, bc , ae ve ef çizgileriyle gösterilmektedir. cd prosesi isehavanın mahal şartlarına kadar ısıtlmasını içerme olup zorunlu bir işlem değildir. Ancak mahalde ısı kazançları yoksa “DA” sevk havasının sevk olunmadan önce mahal şartlarına veya mahallin ısı kaybını karşılayacak düzeye ısıtılması amacıyla düşünülebilir.

5. TEMEL PSİKROMETRİK PROSESLERLER

5.1. PSİKROMETRİK DİYAGRAMDAKİ TEMEL İŞLEMLERİN KISA TANIMI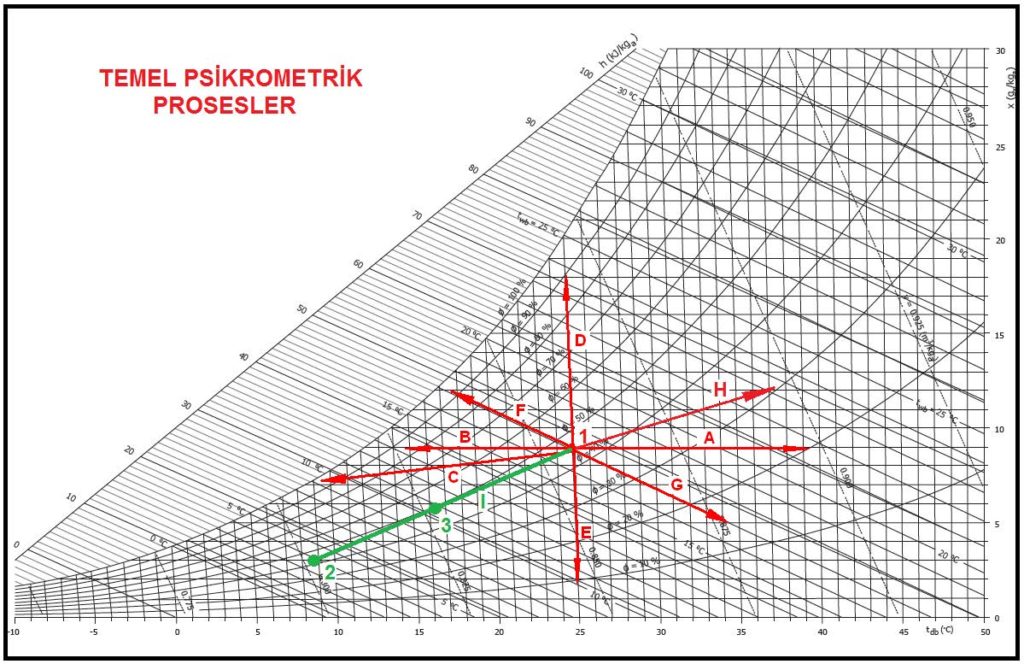

Temel psikrometrik prosesler yukarıdaki psikrometrik diyagram üzerinde gösterilmektedir. Bu prosesleri , diyagramdaki kodlamalara sadık kalarak, aşağıdaki gibi dört ana grupta tanımlayabiliriz:

A- Değişik şartlardaki iki hava kütlesinin karışımı
B- Havanın ısıtılması
– Havanın duyulur ısıtılması (A)
 – Havanın ısıtılması ve nemlendirilmesi (H)
C- Havanın soğutulması
Havanın duyulur soğutulması (B)
 – Havanın soğutulması ve neminin azaltılması (C)
 – Havanın nemlendirilmesi veya neminin azaltılması
D- Havanın izotermik olarak nemlendirilmesi (D)
 – Havanın neminin izotermik olarak azaltılması (E)
 – Havanın yıkanması (adyabatik soğutma) (F)
 – Havanın neminin adyabatik olarak azaltılması (G)

Bu işlemleri 5.2’den başlayarak detaylı bir biçimde inceleyeceğiz.

5.2. DEĞİŞİK İKİ HAVA KÜTLESİNİN KARIŞIMI

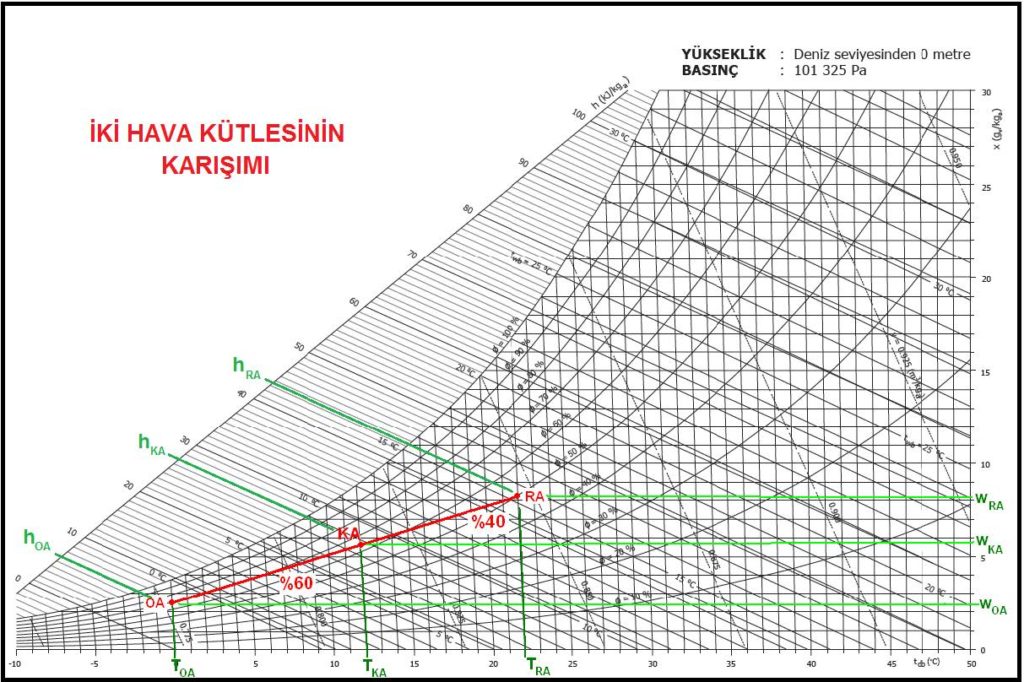
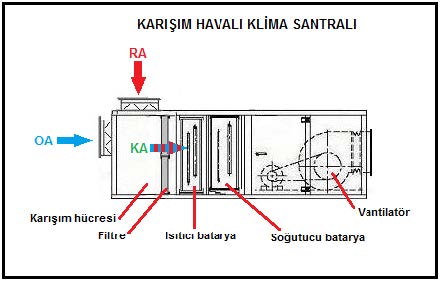
Değişik iki hava kütlesinin karışımı proses olarak yukarıdaki psikrometrik diyagramda ve şematik olarak ta klima santralı çiziminde gösterilmektedir.

Bu proseste iki değişik hava kütlesinin toplamı karışım havasının toplam kütlesini meydana getirmektedir. Keza bu iki kütlenin entalpilerinin toplamı da karışım havasının toplam entalpisini oluşturmaktadır. Bu işlemi şu şekilde ifade edebiliriz.

M_KA = M_RA + M_OA

 M_KA.c_p.t_KA = M_RA.c_p.t_RA + M_OA.c_p.t_OA

t_KA = (M_RA.t_RA + M_OA.t_OA)/M_{KA …………………………………………….}( ^oC)

Bu denklemde özgül ısı “c_p” sabit olduğu için birbirini götürür ve sadeleşerek aşağıdaki duruma dönüşür.

M_KA.t_KA= M_RA.t_RA + M_OA.t_OA

Bu formül sayesinde karışım havası sıcaklığı “t_KA”aşağıdaki gibi bulunur:

t_KA = (M_RA.t_RA + M_OA.t_OA)/M_{KA …………………………………………….}( ^oC)

Aynı şekilde karışım havasının antalpik değeri de aşağıdaki gibi bulunur

h_KA = (M_RA.h_RA + M_OA.h_OA)/M_{KA …………………………………………….}( kJ/kg)

benzeri denklmi mutlak nem oranları için de kurabiliriz.

M_KA.w_KA= M_RA.w_RA + M_OA.w_OA

w_KA = (M_RA.w_RA + M_OA.w_OA)/M_{KA …………………………………………….}( kJ/kg)

Bu işlemlerde “M” kg/h cinsinden hava kütlesini , alt simgeler “_RA”oda havasını veya dönüş havasını,“_OA”dış havayı,“_KA” ise karışım havasını belirtmektedir.

Hesap yoluyla yapılan bu çözümü psikrometrik diyagram üzerinde de yapmak mümkündür. Şöyle ki;

• Dış hava ve iç hava şartlarını Psikrometrik Diyagram üzerinde belirle,
• Belirlediğin iki noktayı bir düz çizgi ile birleştir. Karışım işlemi bu hat üzerinde gerçekleşecektir.
• Çizginin boyunu ölç. Dış hava oranı ile çarp. Çıkan sonucu “RA” tarafından ölçüp hat üzerinde işaretle. Bulduğunuz nokta size karışım havasının özellikleirni verir. Bu noktayı esas alarak, rH, T_db, T_wb, w vehdeğerlerini belirleyebilirsiniz.

ÖRNEK: Dönüş havası şartları 20^oC KT, %50 rH, dış hava şartları 0^oC KT ve %70 rH , dış hava oranı %40 olan bir karışımın şartlarını belirleyin.

Dönüş havası ve dış hava şartları psikrometrik diyagramda belirlenir ve iki nokta birleştirilir. İki nokta arasındaki uzunluğun %40’ı dönüş havası tarafından işaretlenir. Bu nokta karışım şartlarıdır ve psikrometrik diyagramdan okunur (bkz. Psikrometrik Diyagram- İki Hava Kütlesinin Karışımı).

5.3. HAVANIN ISITILMASI

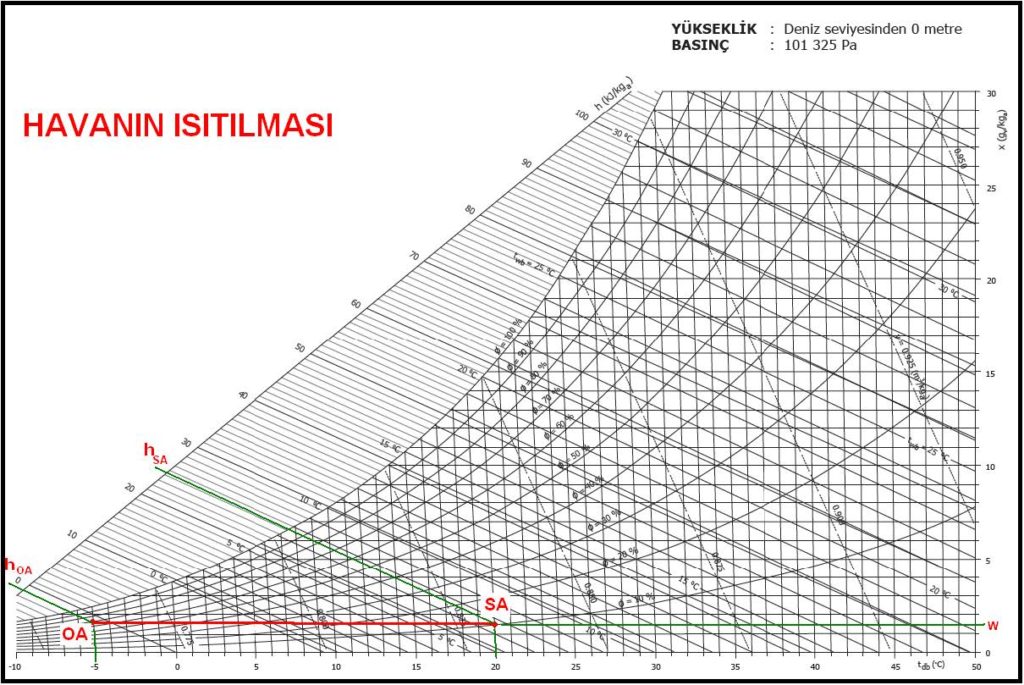
Duyulur ısıtma işlemi havaya ısının transferini içerir. Bu işlem klima santrallarında  ve ısıtma cihazlarında ısıtıcı bataryalar, ısı geri kazanım cihazlarında yalnız duyulur ısı transferi yapan ısı geri kazanım üniteleri, elektrikli ısıtıcılar gibi elemanlarca gerçekleştirilir. Bu işlem esnasında nem alış-verişi olmadığından mutlak nem oranı “W” proses boyunca sabit kalır. Ancak ısıtma işlemi esnasında havanın kuru termometre sıcaklığı artmakta olduğundan bağıl nem devamlı düşüş gösterir. Bunun nedeni de yükselen kuru termometre sıcaklığının doyma noktasının daha yüksek mutlak nem oranlarına tekabül etmesidir. Bu da oarntı neticesi bağıl nemin düşmesidir. Bu proses psikrometrik diyagramda yatay çizgi olarak gösterilir. İşlemi yukarıdaki psikrometrik diyagramda görmektesiniz. Yüzde yüz dış havalı klima santralının şematik çiziminde de “mavi” renkte giren dış havanın ısıtıcı bataryada ısıtıldığı görülmektedir. Çıkan ısınmış hava kırmızı renkte gösterilmektedir.

Bu işlemi analitik olarak aşağıdaki gibi gösterebiliriz:

Q=M.c_p(T_SA-T_OA)

 Q=V.(1/ɤ).c_p(T_SA-T_OA)

 Q=V.(1/ɤ)(h_SA-h_OA)

Yukarıdaki formüllerde kullanılan alt simgeler:

_SA= Üfleme havasını

_OA= Dış havayı simgelemektedir.

 ÖRNEK: 10.000 m³/h dış hava klima santralının ısıtma santralına -5^oC, %70 rH’ta girmektedir. Çıkış şartı ise +20^oC’tır. Çıkış şartındaki bağıl nemi ve bataryanın ısıtma kapasitesini bulun.

Çözümü psikrometrik diyagram üzerinden yaparsak:

H_OA= -1.3 kJ/kg

H_SA= 24.8 kJ/kg

Q=10000 (1/0.800)(24.7+1.3)= 325000 kJ/h bulunur.

Aynı işlemi kuru termometre sıcaklığı üzerinden yaparsak:

Q=10000 x 1.041 (1/0.800)(20+5) = 325313 kJ/h bulunur. (= 96.26KW ) 

5.4. HAVANIN SOĞUTULMASI 

5.4.1. Duyulur Soğutma

Duyulur soğutma işlemi ısıtma işleminin tam tersidir. Bu işlem esnasında havanın yalnız kuru termometre bazında entalpisi azaltılır, mutlak nem oranı sabit kalır. Bu işleme örnek olarak klima santralları içindeki soğutucu bataryaları, fan-coil ve endüksiyon cihazlarındaki serpantinleri ve plakalı eşanjörleri gösterebiliriz.  Bu işlem esnasında çiy noktası sıcaklığına erişilmediği için soğutulan nemli havanın içindeki mutlak nem oranında herhangi bir değişiklik söz konusu değildir.

Bu işlemi analitik olarak aşağıdaki gibi gösterebiliriz:

Q=M.c_p(T_RA-T_SA)

Q=V.(1/ɤ).c_p(T_RA-T_SA)

Q=V.(1/ɤ)(h_RA-h_SA)

Yukarıdaki formüllerde kullanılan alt simgeler:

_SA= Üfleme havasını

_RA= Mahal havasını simgelemektedir.

Duyulur soğutma prosesi aşağıdaki psikrometrik diyagramda gösterilmektedir. Görüldüğü gibi proses boyunca mutlak nem oranı “W”değişmemekte ve sabit kalmaktadır.

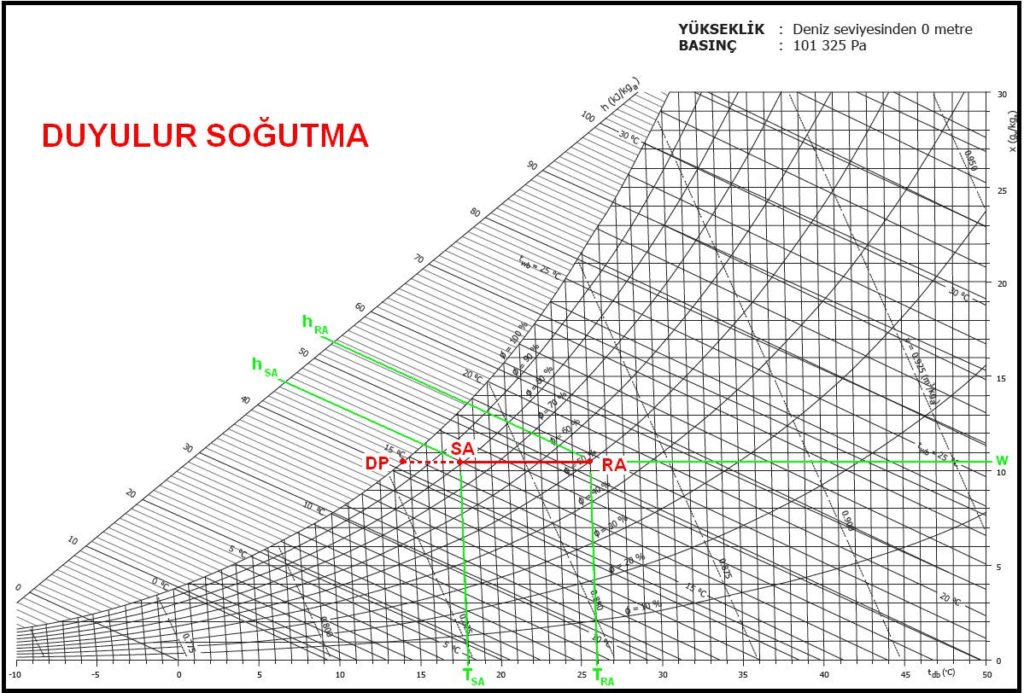
Burada yeni bir tabirle tanışıyoruz. “DP” olarak adlandırdığımız bu nokta çiy noktası veya mahal çiy noktasıdır. Bu nokta mahal şartlarından çizilen yatay bir doğrunun %100 bağıl nem eğrisini yani doyma eğrisini kestiği noktadır. Bu noktaya kadar olan soğutma işlemlerinde havanın mutlak nem oranı değişmez. Bu nedenle bu prosese duyulur soğutma tabir edilir.

5.4.2. Soğutma ve Nem Alma

Soğutma ve nem alma prosesi aşağıdaki diyagramda görüldüğü gibi gerçekleşir. Bu işlem esnasında “OA” olarak belirtilen dış hava başlangıçta duyulur olarak soğur ve bu işlem yatay bir çizgi halinde gerçekleşir. Ancak belirli bir noktaya gelindikten sonra soğutucu bataryanın soğuk satıhları ile temas eden hava içindeki nemi yoğuşma suretiyle bırakmaya başlar. Bu işlem “SA” noktasına varılıncaya kadar devam eder. “SA” noktasını soğutucu bataryanın tasarımı, örneğin toplam ısı transferi alanı, ısı iletim katsayısı ve logaritmik sıcaklık farkı belirler. Bu konuya  ileride aynı bahis içinde daha detaylı bir biçimde değineceğiz.

 

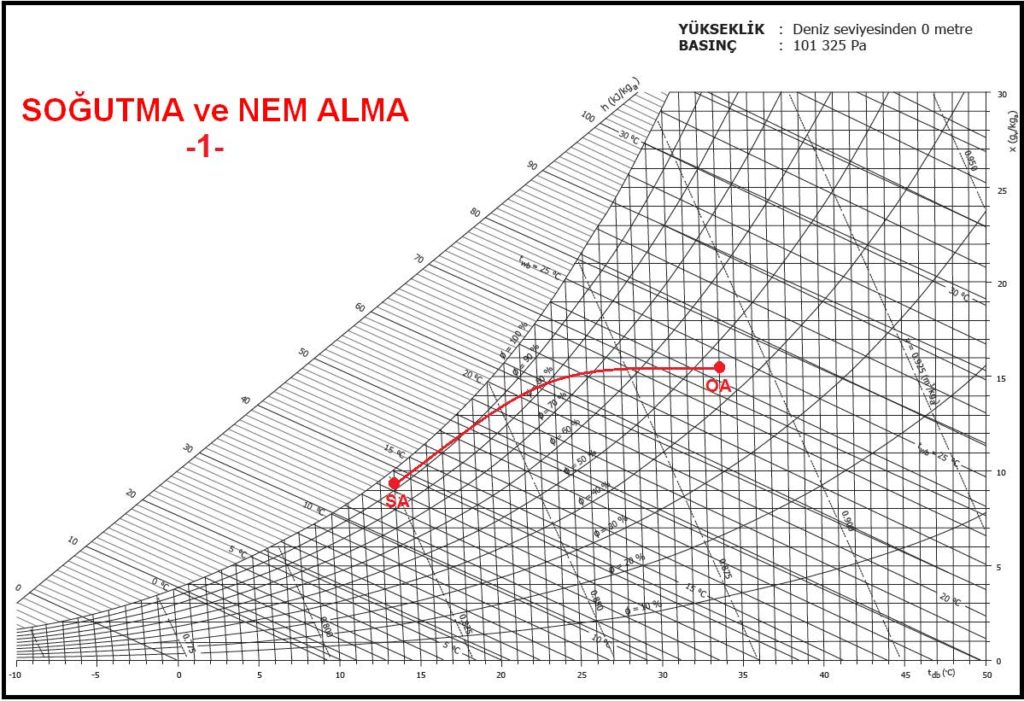
Bu reel prosesi psikrometri açısından incelediğimizde aşağıdaki bulgulara varırız. Bu da gerçekleşen işlemin termodinamik açıdan izahıdır.

Bu proses esnasında hava çiy noktası altında bir sıcaklığa soğutulmak istenmektedir. Ancak salt duyulur soğutma olarak bu mümkün değildir çünkü psikrometrik proseslerde doyma eğrisinin üstünde bir noktaya soğutma mümkün olmadığı için mahal çiy noktası olan “DP”konumuna kadar duyulur olarak soğur, bu noktaya vardıktan sonra hava içindeki nemi  bırakmaya başlar. Bu proses içinde iki değişik işlem yer almaktadır.

• Duyulur soğutma. Bu soğutma esnasında havanın mutlak nem oranı “DP” noktasına gelininceye kadar değişmez. Bu noktadan itibaren soğutma işlemi ile birlikte nem alma işlemi de başlar.
• Mutlak nem oranının azaltılması (izotermik proses). Mahal çiy noktasına erişildikten sonra devam eden soğutma prosesi neticesi hava içindeki nemi yoğuşma suretiyle bırakmaya başlar. Çünkü daha önceki bahislerde gördüğümüz gibi kuru termometre sıcaklığının düşmesi ile kısmi buhar basıncı da düşmekte ve buna bağlı olarak doyma noktasındaki mutlak nem miktarı da azalmaktadır. Soğutma işlemi “ADP” noktasına kadar devam eder.

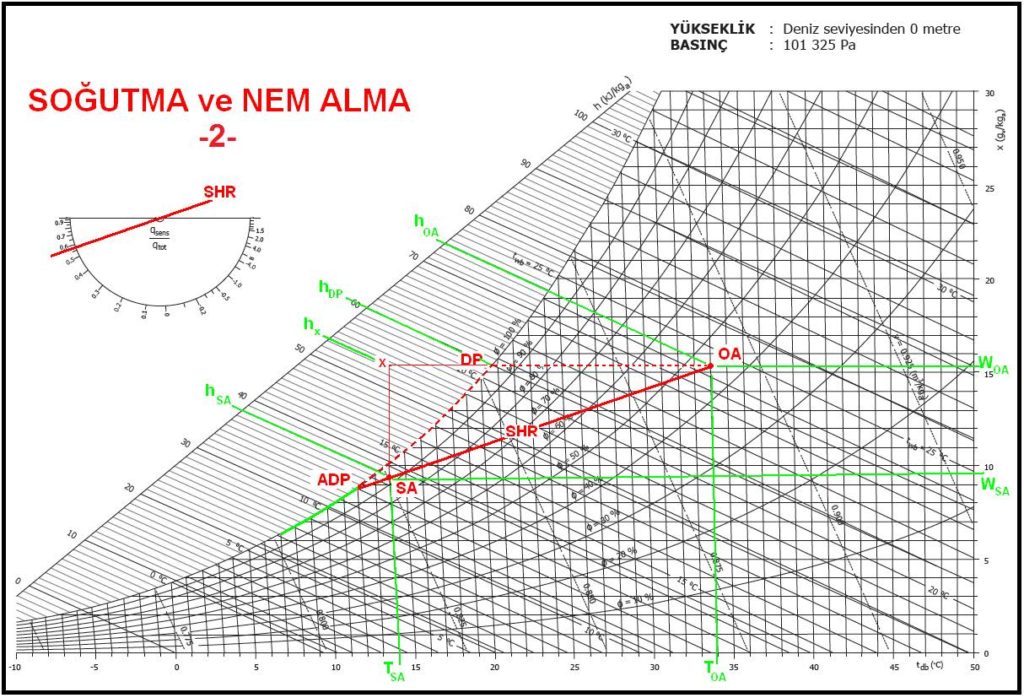
Bunun neticesi olarak karşımıza  eğimli bir proses çizgisi çıkar. Bu çizgi üzerindeki bazı tanımlar bu kitapta karşımıza ilk olarak çıkmaktadır. Bunlardan “DP” “Mahal Çiy Noktası”nı daha önce görmüştük. Buna ilaveten yeni tanımlarımızı şu şekilde özetleyebiliriz:

SHR : Duyulur ısı oranı (proses hattının eğimini belirler)
ADP : Cihaz çiy noktası
SH:  Duyulur ısı yükü
LH:   Gizli ısı yükü
TH:  Toplam ısı yükü
SA:Sevk havası şartları

Duyulur ısı oranı  bir mahallin veya sistemin toplam duyulur ısı kazançlarının ayni mahallin veya sistemin toplam ısı kazançlarına olan oranıdır. 

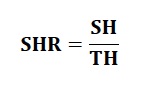
Klima yükü bilindiği gibi duyulur ve gizli ısı yüklerinden oluşmaktadır ve aşağıda gösterilen kalemlerden meydana gelmektedir. Ancak burada bir hususa dikkat edilmesi gerekmektedir. Aşağıdaki tabloda dış havadan, diğer bir ifade tarzı ile taze havadan kaynaklanan ısı yükü gösterilmemiştir çünkü bu yük mahallin  değil, sistemin yükü olarak mütalaa edilmiştir.

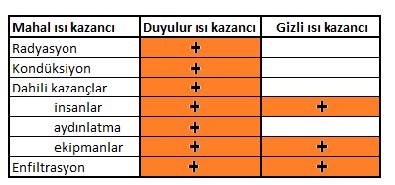
Mahal ısı yüküne dış havadan gelen soğutma yükü de eklendiğinde sistemin toplam ısı yükü belirlenmiş olur. Aşağıdaki tabloda da sistemin duyulur ve gizli ısı kazançları gösterilmiştir. Bu tabloya dış havadan kaynaklanan duyulur ve gizli ısı yükleri de ilave edilmiştir.

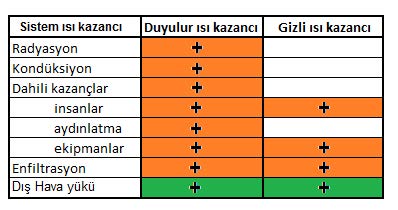
Yukarıdaki tablolardan ve açıklamadan da anlaşılacağı gibi birbirinden farklı iki değişik duyulur ısı oranı mevcuttur. Bunlardan birincisi mahallin duyulur ısı oranıdır. Diğeri de sistemin duyulur ısı oranıdır.

RSHR : Mahal duyulur ısı oranı

ESHR : Sistemduyulur ısı oranı

Sistem ısı kazancının oda ısı kazancından farkı havalandırma için gerekli olan dış havadan gelen duyulur ve gizli ısı yüklerini içermesidir. Bu nedenle iki değer birbirinden farklıdır.

RSHR ve ESHR  değerleri bize soğutma prosesi çizgisinin eğimini belirler. Bu eğimi iki türlü belirleyebiliriz. Bunlardan biri hesap yoluyla, diğeri de psikrometrik diyagramdaki duyulur ısı oranı yarım dairesinden faydalanmak suretiyle.

Hesap yoluyla proses çizgisinin eğimi aşağıdaki gibi saptanır:

Psikrometrik prosesi içeren yukarıdaki diyagramı incelediğinizde “x” olarak belirlenmiş bir hipotetik nokta görürsünüz. Bu nokta aslında yoktur. Yalnızca duyulur soğutma prosesini belirleyebilmek için konulmuştur. OA ile x noktası arasındaki yatay çizgi duyulur soğutma prosesini ve yükünü belirler. Buradaki duyulur soğutma yükünü aşağıdaki gibi belirleyebiliriz.

Q_duy=V.(1/ɤ).c_p(T_OA-T_x)

veya

Q_duy=V.(1/ɤ)(h_OA-h_X)

Aynı şekilde gizli soğutma yükünü de aşağıdaki gibi yazabiliriz.

Q_giz=V.(1/ɤ)(h_x-h_SA)

veya

Q_giz=V.(1/ɤ)(w_OA-w_SA)(h_fg)

h_fg=Suyun normal atmosferik şartlarda buharlaşma (yoğuşma) ısısı.

        (15^oC ve 101325 Pa’da 2465.38 Kj/kg)

Bu iki değer bize dik açılı üçgenimizin iki kenarını verir ve bu sayede “SA”noktasını buluruz.

Diğer bir yöntem ise psikrometrik diyagramlarda bulunan duyulur ısı oranları cetvelidir. Yarım daire tarzındaki bu cetvel diyagramın sol üst köşesinde bulunmaktadır. Burada duyulur ısı oranımızın skala üzerindeki değeri ile yarım dairenin merkezini birleştirerek bir doğu çizer ve bu doğruyu paralel olarak “OA”noktasına taşırız.Bu doğru bizim soğutma proses hattımızdır. Bu hattın %100 bağıl nem çizgisini, yani doyma eğrisini kestiği yer cihaz çiy noktası “ADP”dir. Bu noktayı “DP” ile karıştırmamak gerekir. Biri mahallin çiy noktası, diğeri ise cihazın çiy noktasıdır.

Niye soğutulmuş hava “ADP” şartlarında mahalle sevk olunmamakta, bunun yerine “SA” şartlarında sevk olunmaktadır? Bunun cevabını “by-pass” oranı dediğimiz bir oluşumla açıklayabiliriz. “By-pass”belirli bir orandaki havanın herhangi bir şartlandırmaya tabi tutulmaksızın, hiçbir değişime uğramaksızın geçen miktarıdır. Bunun klimatize tüm havaya oranına da “by-pass oranı”tabir edilir.  By-pass oranı diğer bir ifadeyle kaçak oranıdır. Yalnız ısıtıcı ve soğutucu bataryalarda değil, filtrelerde, damperlerde de by-pass oranları vardır. By-pass oranları, soğutucu bataryanın tasarımına, örneğin sıra sayısına, hava alın hızına, boru ve kanat konfigürasyonuna bağlı olarak %2 ila %10 arasında değişiklik gösterir. Bu by-pass’ın neticesi “ADP” noktasından uzaklaşılır ve “SA” noktasına varılır. Bunu iki değişik hava kütlesinin karışımı olarak ta izah edebiliriz. Örneğin havanın %94’ü ADP şartlarında soğutucu bataryadan çıkmaktadır, %6’sı ise soğutucu batarya ısı transfer satıhlarına değmeden girdiği gibi “OA” lşartlarında çıkmaktadır. Bu iki hava kütlesinin karışımı bize “SA” noktasını vermektedir.

Şu ana kadar anlattığımız işlemi bir örnekle pekiştirelim.

34^oCKT , %45 rH şartlarındaki  10000 m³/h 14^oCKT, %92 rH şartlarına soğutulacaktır.

• Toplam soğutma yükünü
• Duyulur soğutma yükünü
• Duyulur ısı oranını
• Alınan nem miktarını hesaplayınız.

Psikrometrik diyagramdan aşağıdaki termodinamik bulgular alınır.

ɤ_OA= 0.875 m³/kg
w_OA= 0.0154 kg/kg
h_OA= 74 kJ/kg
w_SA= 0.0097 kg/kg
h_SA= 38 kJ/kg

Sistemin toplam soğutma yükü

∑Q= V(1/ ɤ_OA)( h_OA – h_SA)
∑Q= 10.000 (1/0,875)(74-38)
∑Q= 411.428 kJ/h  =  114,265 kW …………..Toplam soğutma yükü
(1 kJ = 0.000277728 kW)
Q_duy= V(1/ ɤ_OA)Cp( t_OA – t_SA)
Q_duy=10.000(1/0.875)1.041(34-14)
Q_duy= 237943 kJ/h = 65,98 kW…………………………Duyulur ısı yükü

SHR= Q_duy/∑Q
SHR= 68,98/114,265 = 0,577=%58……………..Duyulur ısı oranı 

W=V(1/ ɤ_OA)( w_OA – w_SA)
W=10.000(1/0,875)( 0,0154– 0,0097)
W=65,14 kg/h………………………………………….Alınan nem miktarı

Bu arada “ADP” cihaz ciy noktasının önemine değinmek gerekir. ADP soğutucu bataryanın satıh sıcaklığına eşit kabul edilir. Soğutucu bataryanın satıh sıcaklığı da soğutucu akışkanın giriş/çıkış sıcaklıklarıyla yakından ilgilidir. Satıh sıcaklığını belirleyen en önemli unsurdur. Soğutucu bataryalar ekseriyetle ters töne akışlı ısı eşanjörleri olarak tasarlanır ve imal edilirler. “SA” noktası tasarıma tamamen bağlı olmakla birlikte “ADP” sıcaklığını soğutucu batarya satıh sıcaklığına eşit kabul edilir . Soğutucu batarya satıh sıcaklığı da soğutucu akışkanın çıkış sıcaklığına eşit kabul edilir. Bu kabuldeki hata payı çok düşüktür   (± 0,5^oC). Bu nedenle soğutucu akışkan çıkış sıcaklığı ADP’yi ve dolayısıyla proses eğrisini ve duyulur ısı oranını belirler. Eğer duyulur ısı oranınız ve dolayısıyla ADP ve SA önceden belirlenmişse soğutucu akışkan giriş/çıkış sıcaklıklarını belirlemede geniş bir serbestiniz yoktur. Bizim örneğimizde ADP 12^oC olarak belirlenmiştir. Bu nedenle soğutucu akışkan çıkış sıcaklığı da 12^oC alınmalıdır. Aksi taktirde proses daha düşük bir duyulur ısı oranına sahip olacak. Bunun neticesi olarak ta duyulur soğtmada belirgin bir azalma, gizli soğutmada da bir artma meydana gelecektir. Bu uygulamayı ileride, klima santralarını incelerken daha detaylı olarak göreceğiz

5.5 HAVANIN NEMLENDİRİLMESİ

 Havanın nemlendirilmesi iki değişik tarzda yapılmaktadır. Bunlardan birincisi ve en eski metod olan havanın su ile yıkanmasıdır. Diğer metot ta havaya kuru buhar püskürtmek suretiyle nemlendirmedir. Bu iki uygulamayı ayrı ayrı ele alıp inceleyeceğiz.

5.5.1. Havanın Su İle Nemlendirilmesi

 Havanın su ile nemlendirilmesi, diğer bir ifade tarzıyla havanın yıkanması aynı zamanda havanın adyabatik soğutulması da demektir. Havanın su ile nemlendirilmesi işlemi klima santralları içinde yapıldığı gibi direkt mahallerde de yapılmaktadır. Örneğin bazı tekstil fabrikalarında, iğ tesislerinde mahallere basınçlı hava ile  su borular vasıtasıyla sevk edilmekte, mahalle yerleştirilmiş nozullar vasıtasıyla püskürtülmektedir.

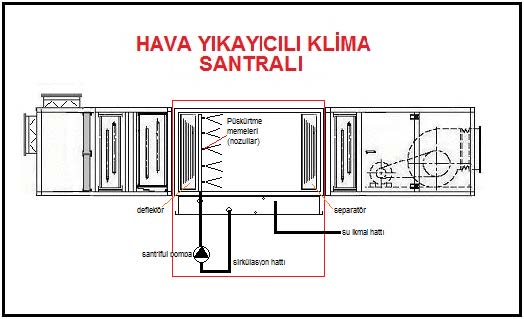
Klima santralları içinde iki değişik yöntem kullanılmaktadır. Bunlardan birincisi, klasik bir yöntem olan suyun pulverize bir şekilde havanın içine püskürtülmesidir. Bu sistemde yüksek debilerde su havanın içine püskürtülmekte, ancak bu suyun çok az miktarı buharlaşıp havaya karışmaktadır. Bakiye su, havuz tabir ettiğimiz haznede toplanmakta, buradan bir pompa vasıtasıyla tekrar nozullara sevk edilmekte ve püskürtülmektedir. Sistem şematik olarak aşağıda görülmektedir. Hava yıkayıcısı kırmızı dikdörtgen içinde görülmektedir.

Klima santrallarında uygulanan diğer bir yöntem de dolgu tipi (matt type) nemlendiricilerdir. Bu uygulamada havanın içine doğrudan su püskürtülmesi yerine havanın ıslatılmış satıhlarla teması sağlanmıştır. Daha az hacım gerektiren bu uygulamada nozullar da küçültülmüş neticede sirkülasyon pompası da küçültülmüştür. Büyük ölçüde enerji tasarrufu sağlayan bu uygulama günümüzdeki adyabatik soğutma ve nemlendirme işlemlerinde tercih edilmektedir.

 

Adyabatik soğutma ve nemlendirme işlemi yaz aylarında bağıl nemi düşük olan yerlerde hava soğutucusu- klima cihazı olarak kullanılmaktadır. Ülkemizde bu uygulamaya müsait bölge olarak Güneydoğu Bölgemizi gösterebiliriz.

Aynı işlem su soğutma kulelerinde de uygulanmaktadır. Soğutma gruplarının su soğutmalı kondenserlerinden çıkan ısınmış su santrifuj pompalar vasıtasıyla soğutma kulesine sevk edilmektedir. Soğutma kulesinde su pulverize bir tarzda dolgu elemanlarının üzerine püskürtülmekte ve bu elemanların sathını ıslatmaktadır. Hava ile temas eden suyun belirli bir oranı buharlaşmakta, gerekli ısıyı da sudan almaktadır. Bu sayede soğutma kulesine sevk olunan su istenen derecede soğumuş olarak kondensere pompalanmaktadır. Soğutma kulelerinin en büyük avantajı soğutma gruplarına göreceli olarak daha düşük kondansasyon sıcaklıklarında çalışma olanağı sağlamak ve bu suretle soğutma verim ve kapasitesini arttırmaktır. Dezavantajı ise buharlaşma neticesi devamlı su kaybına sebebiyet vermektir.

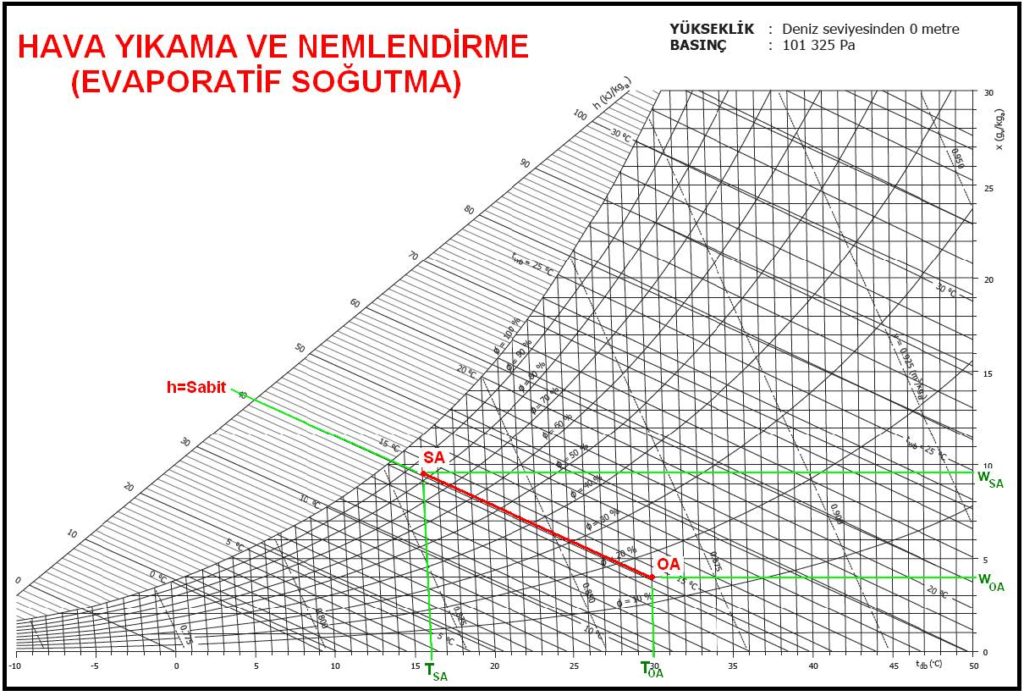
İster havaya su püskürtme metodu ile nemlendirme, isterse dolgu tipi nemlendirme olsun her ikisi de psikrometrik proses olarak birbirinin aynıdır ve aşağıdaki psikrometrik diyagramda görüldüğü gibidir.

 

Aşağıdaki resimde su-hava karışımını püskürten nozullar görülmektedir.

Buradaki temel işlem adyabatik olduğundan püskürtülen su buharlaşmak için gerekli ısıyı su ve havadan almaktadır. Bu işlem esnasında her ikisi de kakrlı rejim olarak ifade edeceğimiz bir duruma gelmekte, suyun sıcaklığı havanın adyabatik soğutma sonucu varacağı doyma sıcaklığına eşit olmakta, havanın sıcaklığı ise nemlendiricinin verimi oranında bu sıcaklığa yaklaşmaktadır. Hava yıkayıcılı nemlendiricilerde verim %70 ila %95 arasındadır. Verimi belirleyen hususlar içinde hava yıkayıcı hücresinin uzunluğu, havanın hızı, püskürtülen su miktarının havaya orantısı ve pulverizasyon işlemi sonrası meydana gelen tane büyüklüklerini gösterebiliriz.

Dolgu tipi nemlendiricilerde verim daha yüksektir, %85 ila %95 arasında oluşmaktadır. Bunun nedeni de ıslak satıhlar nedeniyle havanın daha fazla su zerreciği ile temasta olabilmesidir.

5.5.2. Havanın Buhar İle Nemlendirilmesi

Buhar ile nemlendirme izotermik bir proses olarak tanımlanır. Havaya doğrudan buhar ilave ettiğiniz için yalnız havanın mutlak nem oranını arttırmakta olduğumuz için bu proses teorik olarak izotermik kabul edilir. Psikrometrik diyagramdaki prosesler standart basınç ve sıcaklığa bağlı olarak, örneğin 101,325 Pa ve 15^oC KT için belirlendiğinden, havaya püskürtülen buharın da bu sıcaklıkta olduğu kabulü ile bu varsayım doğrudur. Ancak proses hakikatte, üflenen buhar sıcaklığına ve özgül entalpisine bağlı olarak hafif sağa yatan bir doğru tarzında oluşur. Buharın sıcaklığının mahal sıcaklığının çok üstünde olması nedeniyle  üflenen buhar nemlendirme işlemine ilaveten havayı da , az da olsa, ısıtmış olacaktır. Çünkü üflenen buharın sıcaklığının ortam sıcaklığından yüksek olması ortam sıcaklığındaki üflenen buharın özgül entalpisinin de ortam sıcaklığındaki buharın entalpisinden yüksek olması demektir. Termodinamiğin birinci kanununa göre enerji yok edilemeyeceğine veya yaratılamayacağına göre üflenen buhardaki fazla entalpi havanın ısınmasına neden olur. Bir başka ifade tarzı ile buhar ve hava karışımı nem açısından olduğu gibi kuru termometre sıcaklığı açısından da bir denge oluşturacaklardır.  Bu oluşumu ve buharla nemlendirmeyi aşağıdaki örnek ve diyagramda gösterebiliriz.

Örnek-1: 15^oCKT sıcaklığındaki mahalle oda sıcaklığında kuru buhar kontrollu olarak püskürtülmektedir. İstenen mutlak nem oranını  0,009 kg_wv/kg_daseviyesine kadar yükseltmektir. Prosesi belirleyiniz.

Burada karşımıza psikrometrik diyagramda yeni bir skala çıkmaktadır. Bu skala “Δh/Δw” skalasıdır. Bu skala Willis Carrier tarafından bulunan ilk psikrometrik diyagramlarda yoktu. Ancak daha sonraki yıllarda Prof. Mollier tarafından çıkarılan i-x diyagramında bu skala vardı. Geçen yıllar içinde ASHRAE de aynı skalayı kendi diyagramlarına eklemiştir.

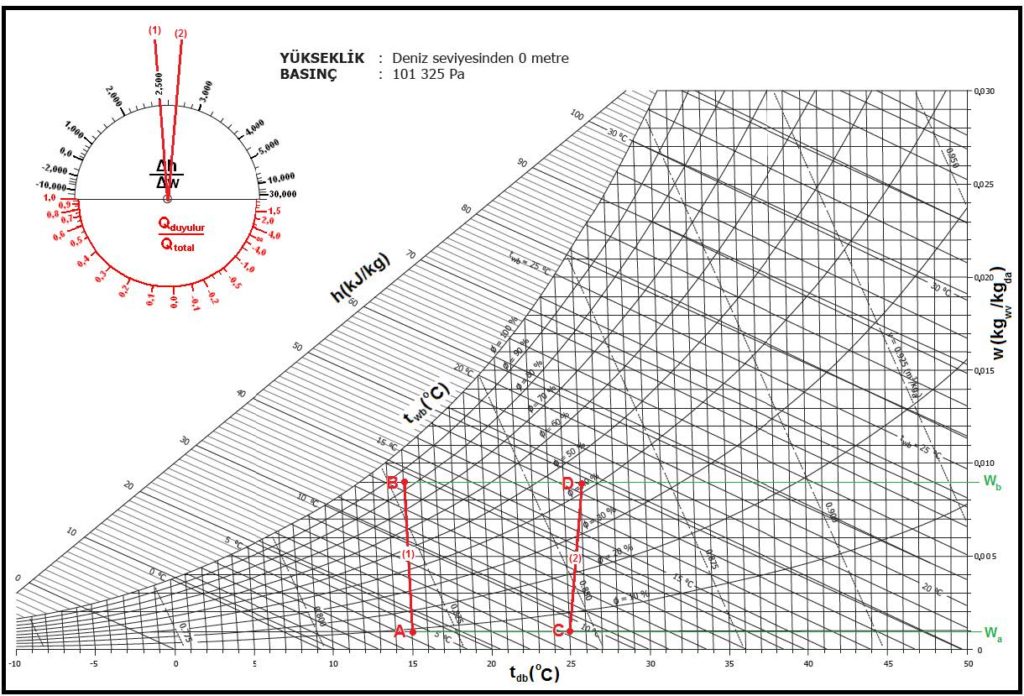
Bölüm-2, Konu 2-3’deki Tablo-2’den su buharının 15^oC’taki özgül entalpisi 2528.36 kJ/kg olarak bulunur. Psikrometrik diyaramın sol üst köşesindeki “Δh/Δw” skalasında dairenin merkez noktası çember üzerindeki 2528.36 noktası ile düz bir çizgi olarak birleştirilir. Bu çizgi paralel olarak “A” noktasına taşınır.Bu bizim “A” ile B” noktaları arasındaki proses hattımızdır. Diyagramdan da görüldüğü gibi proses çizgisi tamamen izotermik bir özellik taşımaktadır.

Örnek-1: 25^oCKT sıcaklığındaki mahalle 130^oC kuru buhar kontrollu olarak püskürtülmektedir. İstenen mutlak nem oranını 0,009 kg_wv/kg_daseviyesine kadar yükseltmektir. Prosesi belirleyiniz.

Bir önceki örnekte yaptığımız gibi Bölüm-2, Konu 2-3’deki Tablo-2’den su buharının 130^oC’taki özgül entalpisi 2720.09 kJ/kg olarak bulunur. Psikrometrik diyaramın sol üst köşesindeki “Δh/Δw” skalasında dairenin merkez noktası çember üzerindeki 2720.09 noktası ile düz bir çizgi olarak birleştirilir. Bu çizgi paralel olarak “C” noktasına taşınır.Bu bizim “C” ile D” noktaları arasındaki proses hattımızdır. Diyagramdan da görüldüğü gibi proses çizgisi tam bir izotermik görünümsde değildir. Çünkü mahalle ilave edilen buhar yalnız mutlak nem oranını arttırmakla kalmamış, havayı da belirli bir ölçüde ısıtmıştır.

Buharla nemlendirme klima santralı ve hava kanalı içine kondens ayırıcılı özel nozullar vasıtasıyla yapılabildiği gibi mahallere de doğrudan püskürtülebilmektedir. Sistemde buhar mevcutsa, örneğin hastaneler, büyük oteller gibi mutfak ve çamaşırhane içeren tesislerde, kondensi ayrıştıran, bünyesinde separatör ve kondenstop bulunan püskürtücüler kullanımıyla bu işlemi gerçekleştirebiliriz. Bu uygulama aşağıdaki resimde görülmektedir.

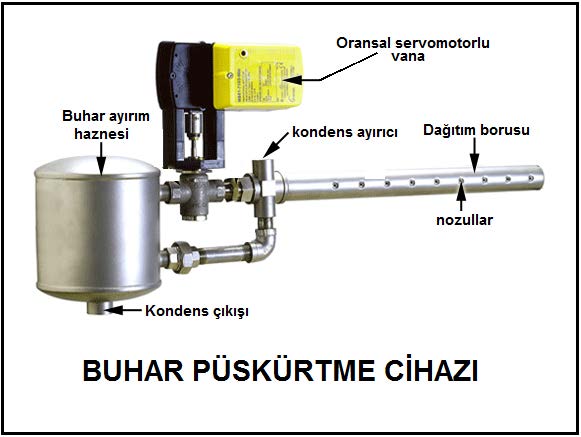
Eğer buhar mevcut değilse bünyesinde buhar jeneratörü kullanan buharlı nemlendirme aparatları kullanmamız gerekecektir. Aşağıdaki resimde görülen jeneratörlü buharlı nemlendirme aparatı bünyesinde bir veya birden çok buhar haznesi bulundurmaktadır. Uçkları siyah olarak görülen elektrodların suyun içine daldırılması suretiyle su buharlaştırılmakta ve mahalle (klima santralına, hava kanalına veya odaya) yukarıda görülen buhar püskürtme cihazı ile püskürtülmedir. Elektrodlu nemlendiricinin bünyesinde otomatik kontrol donanımı genelde bulunduğu için ayrıca bir moransal servomotorlu vanaya ihtiyaç duyulmamaktadır.

Buharlı nemlendiriciler çok az yer kaplamaları ve kolay montajları nedeniyle günümüzde yaygın olarak kullanılmaktadırlar. Elektrodlu paket tip buharlı nemlendirici cihazı üretici firmalarından CAREL, silindirden buhar çıkış sıcaklığını 102 ila 103^oC olarak vermekte, borulama ve nozulda meydana gelmesi muhtemel soğumalarla bu sıcaklığın 100^oC alınmasını önermektedir.

Son derece pratik olan elektrodlu buharlı enmlendiricilerde kullanılan suyun sertlik  derecesi çok büyük önem taşımaktadır. Çünkü suyun sertliği elektrod ve silindirlerde kireçlenmeye ve verimin düşmesine neden olmakta ve cizahın faydalı ömrünü kısaltmaktadır.

5.6.FAN EFEKTİ

Fan efekti hava hareketinin elektrik motoru ile tahrik edilen elemanlarca, örneğin vantilatör ve aspiratörlerle donatılmış cihazlarda, klima ve havalandırma santralarında, fan-coil cihazlarında görülen bir duyulur ısı kazancı prosesidir.  Elektrik motorlarında verim %100 değildir. Günümüzdeki motorlarda bu verim %90’ın üzerindedir. Elektrik motoruna verilen elektrik enerjisinin verime bağlı olanı işe dönüşür. Bakiye, yani “1-η” vantilatör ve aspiratörlerde gövde ısınması, kayış-kasnaklı olanlarda kayma-sürtünmeden meydana gelen ısınma neticesi sevk olunan ve/veya döüş havasının belirli bir oranda ısınmasına neden olur. Kış klimasında bir emniyet faktörü olarak kabul edilen bu durum yaz uygulamalarında dikkate alınmalıdır.

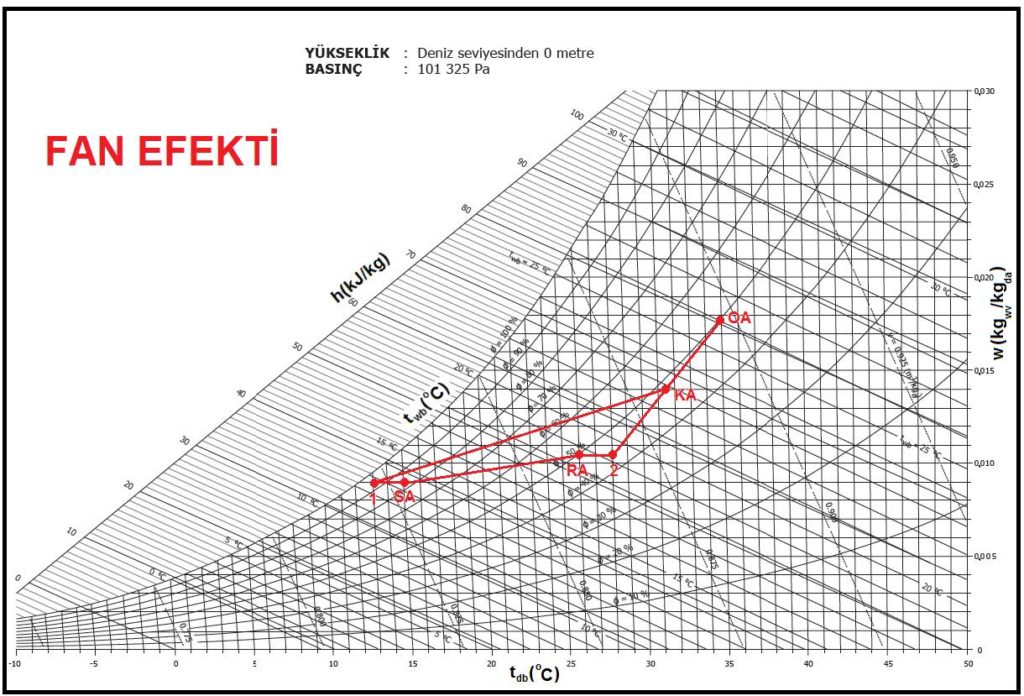
Yukarıda fan efekti olan tipik bir yaz klima prosesi görülmektedir. Bu proseste “OA” dış havayı, “RA” mahal havasını, “KA” karışım havasını, “SA” ise mahalle sevk olunan klimatize havayı ifade etmektedir. “KA-1” prosesi ile “1” şartlarına kadar soğutulan hava vantilatör vasıtasıyla mahalle sevk olunmaktadır. Ancak bu noktada yukarıda belirtilen nedenlerle bir miktar ısı havaya transfer olunmakta ve duyulur ısınma yaratmaktadır. Benzeri bir işlem de aspiratörde vukuu bulmaktadır. Mahal şartlarında emilen havaya aspiratör ve elektrik motorundan ısı geçişi olmaktadır. Bu nedenle karışım “RA-OA” arası olması gerekirken “2-OA” arası gerçekleşmektedir. Proje müellifi mühendislerin bu hususu incelemeleri ve bu hususta bir karar vermeleri gerekmektedir. Çoğu zaman fan efekti %1 civarında ve hatta bunun da altında olduğu için ihmal edilmektedir.

5.7. ODA EFEKTİ

Oda efekti, yaz klimasında “SA-RA” arasındaki prosestir. Bu proses ısınma ve ısınırken nem kazanmayı içermektedir. Oda duyulur Isı Oranı “RSHR” na bağlı olan bu işlem Konu 5.4.2’de anlatılmıştır. Benzeri bir işlem de kış klimasında gerçekleşmektedir.

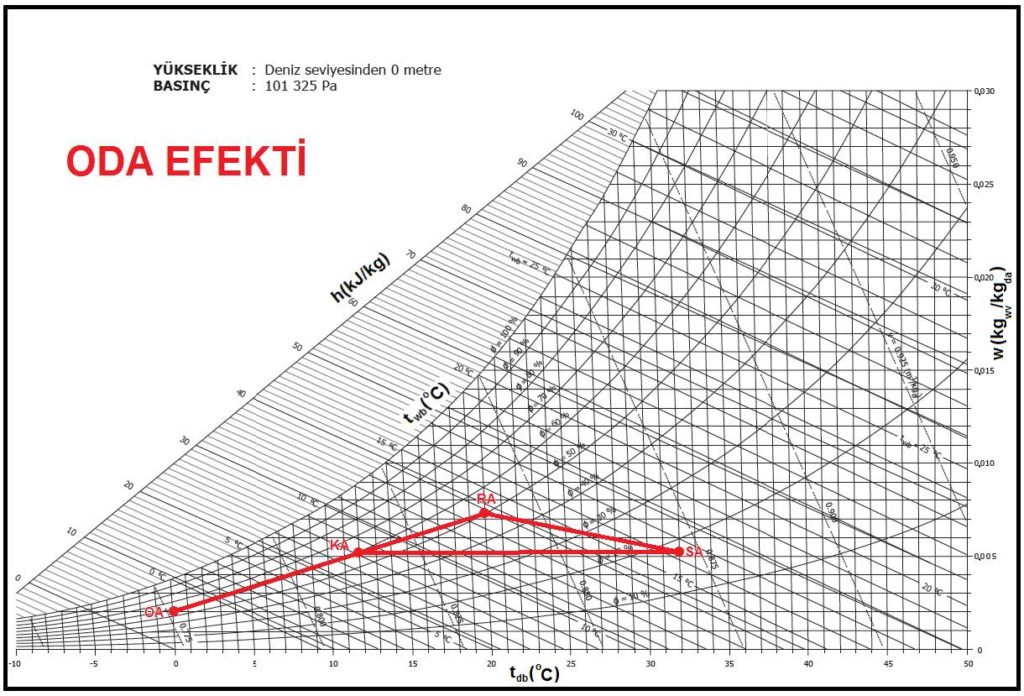
Kış oda efekti karaışım noktası “KA”dan üfleme noktası “SA”ya kadar ısıtılan havanın mahal şartlarına kadar soğurken nem kazanmasını içerir. Karışım havası hava dış havanın ısıtılması ile mahal ısı kaybının karşılanması için “SA” noktasına kadar ısıtılmaktadır. Bu noktada mahalle sevk olunan hava mahallin ısı kaybı neticesi mahal şartlarına kadar soğuyacaktır. Ancak bu soğuma işlemi esnasına nem kazanacaktır. Bu nem kazanma işlemi dahili kazançlara , örneğin içerdeki insan sayısına bağlıdır. “SA-RA” proses hattı bu soğuma ve nemlenme işlemini göstermektedir. Bu prosesin iyi hesaplanması birçok uygulamada buharlı veya sulu nemlendiricileri gereksiz kılabilir.

5.8. DUYULUR ISI ORANI DÜŞÜK UYGULAMALAR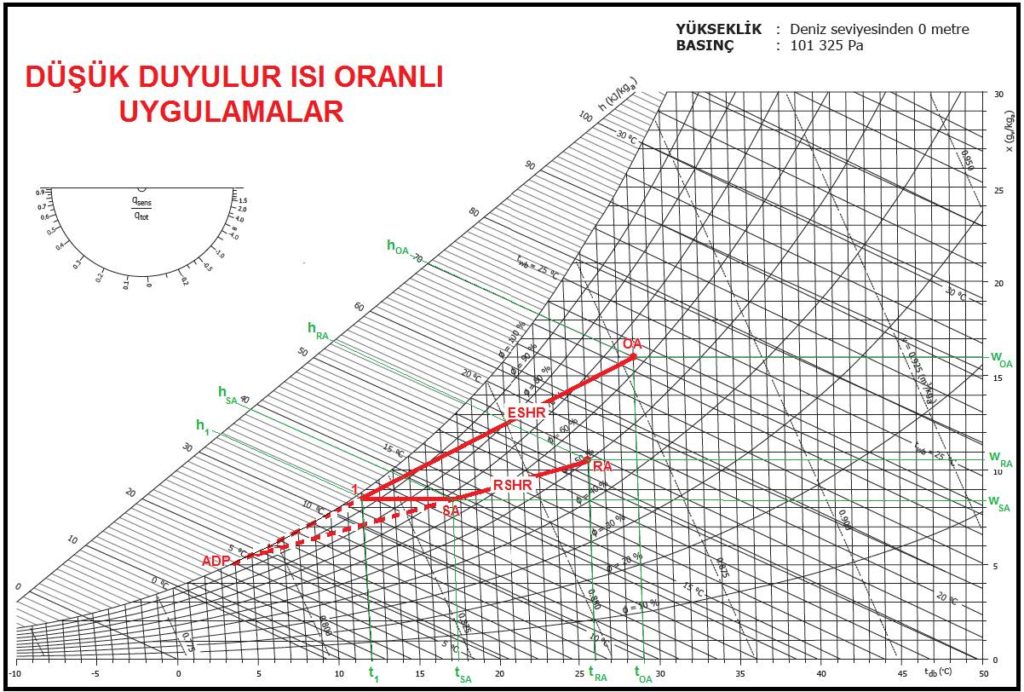 

Sinema ve konser salonu, gece klüpleri gibi insan sayısı fazla, bu nedenle gizli ısı yükü yüksek olan mahallerde istenen hava debisinin tespitinde, üfleme sıcaklığının istenen sınırlar dahilinde tutulmasında zorluklar yaşanmaktadır. Bu zorluklar dahili ısı kazançlarındaki yüksek gizli ısı yükünden kaynaklanmaktadır. Bu işlemi bir örnekle izah etmek daha iyi olur.

Örnek: 300 m²büyüklüğünde, bir otelin bodrumundaki gece klübü saat 22.00’dan sonra çalışmaktadır. Gece klubü 200 kişiliktir.  Gündüz maksimum sıcaklık 36^oCKT, %38 rH’dır. Saat 22.00’deki sıcaklık düşümünün 6^oC olduğu kabulüyle klima santralı büyüklüğünü ve yükleri belirleyiniz:

-Dış hava : 30^oCKT, 22,5^OCYT, %53 rH, W_DH= 0.0145kg_WV/kg_DA,,h_DA=73,5 kJ/kg

-İç hava   : 26^oCKT, 18,7^OCYT, %50 rH, W_DH= 0.0105kg_WV/kg_DA,,h_DA=53,0 kJ/kg

-26^oC’ta buharlaşma ısısı h_fg= 2441,71 kJ/kg

(1,00 kJ/kg = 0,277728 Watt = 0,00027773 kW = 0,238846 kCal/h

                                                                     DUYULUR ISI        GİZLİ ISI

• 100 kişinin masada oturduğu (kabul)… 70 W/kişi.h ……….45 W/kişi.h
• 100 kişinin dans ettiği (kabul)…………… 90 ………160
• Aydınlatma yükü ………..……………………..10 W/m²

Örneğimizde gece klubünün herhangi bir kondüksiyon ve radyasyon yükü olmadığı. Enfiltrasyonun da pozitif basınçla önlendiği kabul edilmiştir.

Bu duruma göre yüklerimiz aşağıdaki gibi hesaplanır ve bulunur.

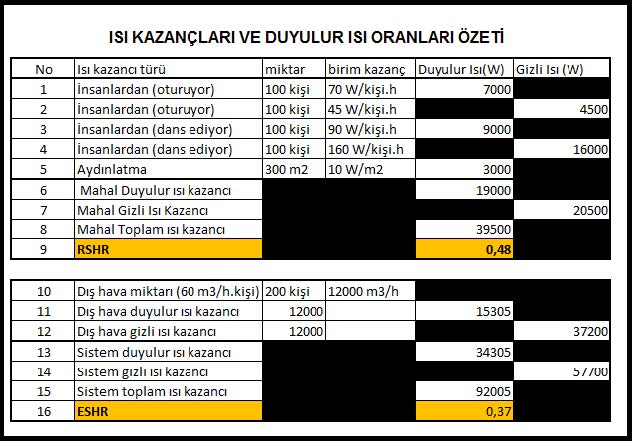
Bu hesaplardan hareket ettiğimizde ve bu bulgulara göre prosesi psikrometrik diyagrama işlediğimizde iki yanlışlık ile karşılaşırız.

• RSHR ve ESHR hatları doyma eğrisini kesmemektedir. Bu mümkün değildir.Daha önce 5.4.2 No.lu “Soğutma ve Nem Alma” konusnda da bahsettiğimiz gibi soğutma prosesi eğrisi doyma eğrisi ile kesişmelidir. Doyma noktası üzerinde buluna ADP noktası ile soğutucu bataryaya giriş noktası arasında (örneğimizde “OA”) by-pass faktörünü içeren bir karışım söz konusudur.
• ADP noktası aynı zamanda soğutucu akışkanın soğutucu bataryadan çıkış şartlarını da belirlemektedir. Aşağıda görülen proseste ADP noktası bulunamadığından hangi soğutucu akışkanın hangi giriş/çıkış şartlarında kullanılacağı da cevapsız kalmaktadır.
• Gerekli hava debisinden yola çıkarak “SA” noktasının bulunması:

• İkinci önemli bir husus ta bulunan “SA” noktasıdır (21,5^oC). Bu sıcaklık neticesinde istenen 12000 m³/h hava debisine yakın bir debi çıkmaktadır. Ancak ESHR proses çizgisinin doyma eğrisini kesmemesi nedeniyle bu noktanın yakalanması mümkün değildir.

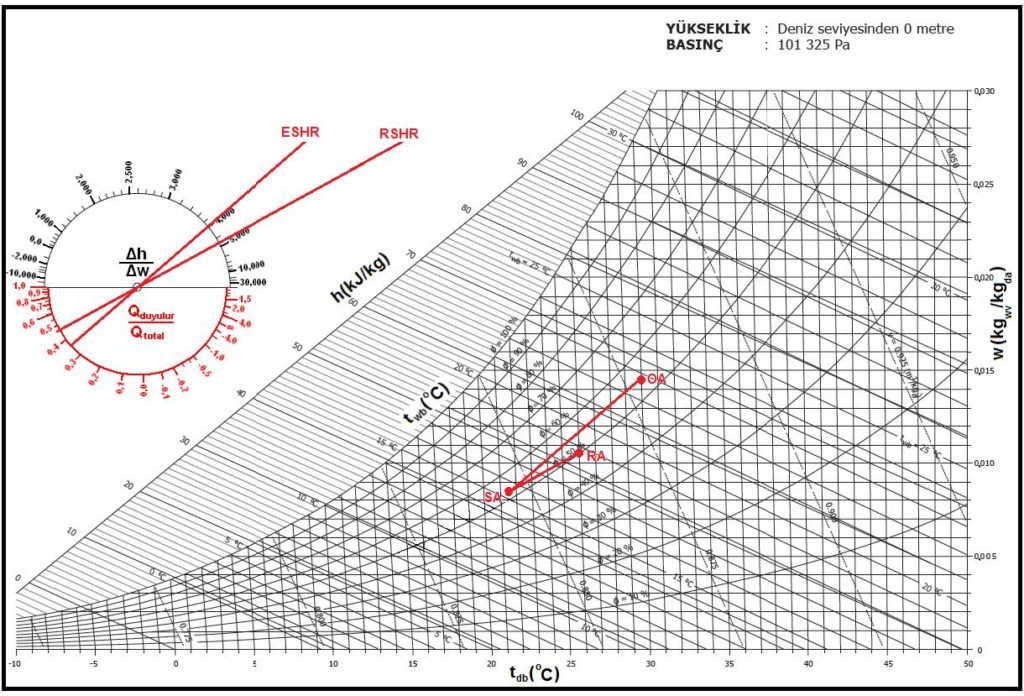
Uygulaması mümkün olmayan, hayali tabir edeceğimiz proses aşağıda görülmektedir.

Bu durumda yapılması gereken işlem dış hava “OA”nın belirli bir noktaya kadar, doyma eğrisini kesecek tarzda bir prosese sahip olmasını temin etmek, bu noktadan sonra soğutulmuş havayı “SA” noktasına kadar ısıtmaktır. Bu işlem sonunda “SA” noktasında mahalle sevk olunacak hava mahal içinde “oda efekti” neticesi ısınacak ve ısınırken dahili kazançlar neticesi nem de kazanacaktır. Yani “RSHR” hattı doğrultusunda bir işleme tabi olarak mahal şartları “RA”yı gerçekleştirecektir. Bu işlem aşağıdaki psikrometrik diyagramda gösterilmektedir.

Gerekli hava debisinin nasıl hesaplandığını bir önceki sayfada görmüştük. “RA” şartlarından çizeceğimiz “RSHR” hattının “SA” kuru termometre hattı ile kesiştiği nokta bizim “SA” mahalle klimatize havanın sevk olunacağı durumdur. “SA” noktasından hareketle yatay bir hat çizeriz. Bu hat bizim soğutma sonrası yapacağım son ısıtma (reheat) prosesidir. Mühendislik kabulü ile bu hat üzerinde bir “1” noktası belirleriz. Bu nokta ADP ile OA konumlarının by-pass neticesi karışım noktası olacaktır. Şimdi “ADP-OA” prosesini çizebiliriz. “OA” ile “1”i birleştirdiğimizde bu doğrunun doyma eğrisini kestiği nokta “ADP” konumudur. “ADP” konumunu aynı zamanda soğutucu akışkanın bataryadan çıkış sıcaklığı olarak ta kabul edebiliriz.

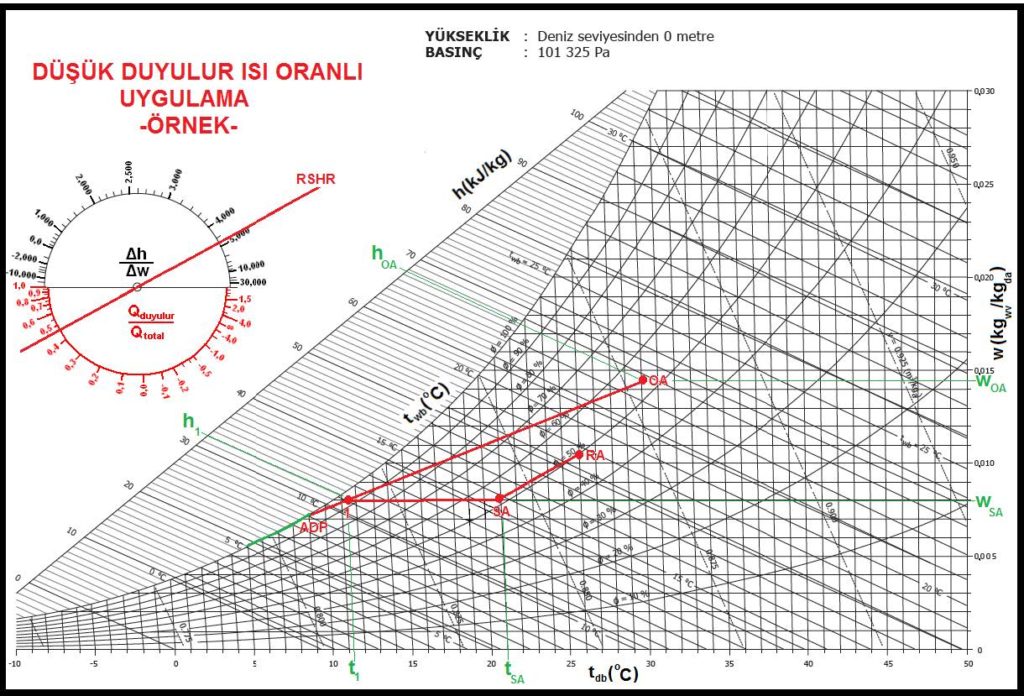
Eğer soğutucu akışkan olarak soğuk su kulanacaksak, en çok uygulanan 4 ila 5^oC giriş/çıkış faklarından 4^oC’ı kabul edersek soğuk su rejimimiz 5/9^oC bulunur. Soğuk su yerine direkt genleşmeli batarya kullancaksak bu sefer ADP’yi evaporasyon sıcaklığı ile aşırı kızdırma (superheat) sıcaklıklarının toplamına eşit alabiliriz.   Bu durumda evaporasyon sıcaklığı +5^oC, aşırı kızdırma sıcaklığı da 4^oC olmalıdır.

Burada bir şeye dikkat etmek gerekir. Satıh sıcaklığının 0^oC civarında olması özellikle kısmi kapasite kullanımlarında karlanma ve kardanmadan dolayı bataryada tıkanmaya neden olacağından mümkün olduğunca artı değerlerde sıcaklıkların seçilmesine gayret gösterilmelidir.

Burada dikkat edilecek bir husus ta bu tip uygulamalarda kış klima uygulamasıdır. Özellikle dış hava sıcaklığının 0^oC’ın altında olduğu yerlerde, eğer soğuk sulu soğutma bataryası kullanılıyorsa donma riskini önlemek için iki ısıtıcı batarya kullanılması önerilir. Bu bataryalardan biri soğutucu bataryadan önce yerleştirilecekit ve görevi yalnız kış klimasında dış havayı ısıtmak olacaktır. Bu batarya yaz kliması uygulamalarında çalışmayacaktır.

Aşağıda donma riski bulunmayan bir klima santralı yerleşimi şematik olarak gösterilmektedir.

Aşağıda da donma riski bulunan ve sulu soğutma serpantini kullanan bir klima santralı yerleşimi şematik olarak görülmektedir.

Bu uygulamadaki ön ısıtıcı batarya yalnız kış ısıtmasında kullanılmaktadır. Soğutma ve nem almanın gerektiği yaz aylarında ve geçiş mevsimlerinde devre dışı kalmaktadır. Son ısıtıcı batarya ise soğutucu batarya ile birlikte soğutma ve nem alma işlemlerinde kullanılmaktadır.

4. PSİKROMETRİK DİYAGRAMLAR

4.1. GENEL

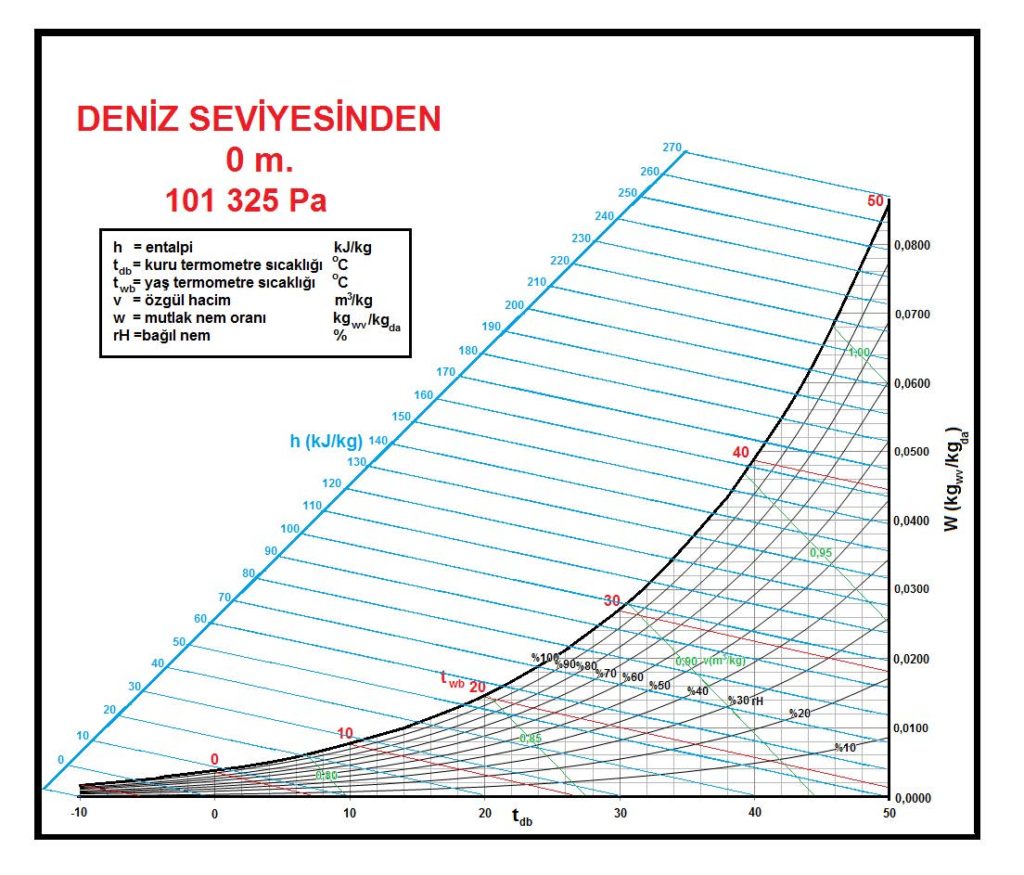
İlki 1904 yılında Willis Carrier tarafından yapılan ve günümüze kadar, araştırmalar neticesi devamlı gelişme gösteren Psikrometrik Diyagramlar nemli havanın termodinamik özelliklerinin yansıtıldığı tablolardır. Ancak bu tablolarda entropi ve buhar basıncı gösterilmez. Ancak buhar basıncının mutlak nem oranı ve doyma noktası ile olan matematiksel ilişkisi nedeniyle biz psikrometrik diyagramlarımıza buhar basıncını mutlak nem oranı ordinatına paralel bir çizgi olarak ekledik.

-40^oC ile +120^oC aralığı ve 101.325 kPa atmosferik basınç için tek bir diyagram hazırlamak mümkündür.

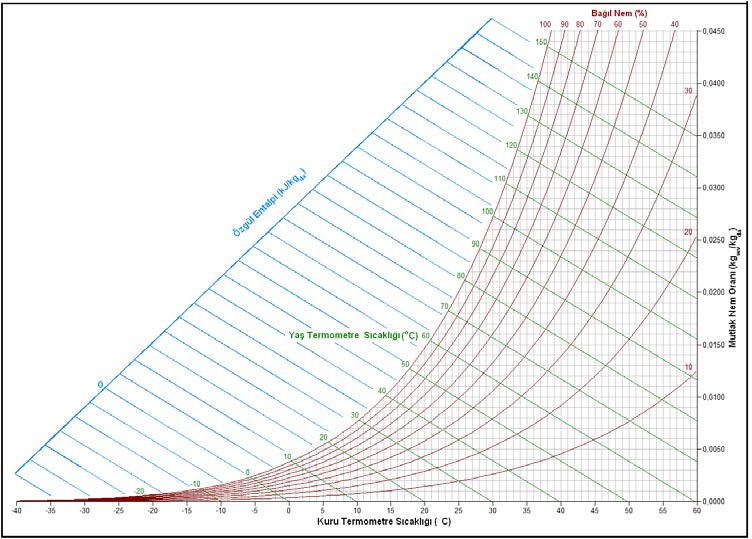
Ancak bu diyagramda normal ve düşük sıcaklıklardaki değerleri, örneğin A4 veya A3 ölçülerindeki bir psikrometrik diyagramda okumak çok zor olacağından ASHRAE bunu üçe bölerek kolaylaştırmıştır. Birinci tablo 0^oC ila 50^oc arasındaki sıcaklıklara, konfor klimasının genelde uygulamasının yapıldığı şartlara hitap etmektedir. Bunu tamamlayıcı mahiyette iki psikrometrik diyagram daha bulunmaktadır. Bu diyagramlardan biri -40^cC ila +10^oC aralığına hitap eden “düşük sıcaklık” psikrometrik diyagramıdır. Diğeri ise “yüksek sıcaklık”diyagramıdır. Bu diyagram +10^oC ile +120^oC aralığını kapsamaktadır. Yüksek sıcaklık psikrometrik diyagramı özellikle yüksek sıcaklıklarda ısı geri kazanımı prosesleri ile absorbsiyonlu nem alma proseslerinin etüdü açısından çok faydalı olmaktadır. Bu diyagramların tamamı 101.325 kPa basınca tekabül eden deniz seviyesi içindir. Birinci bölümde bahsedilen konulardaki formüllerle değişik irtifalar için de psikrometrik diyagramların çizimi mümkündür.

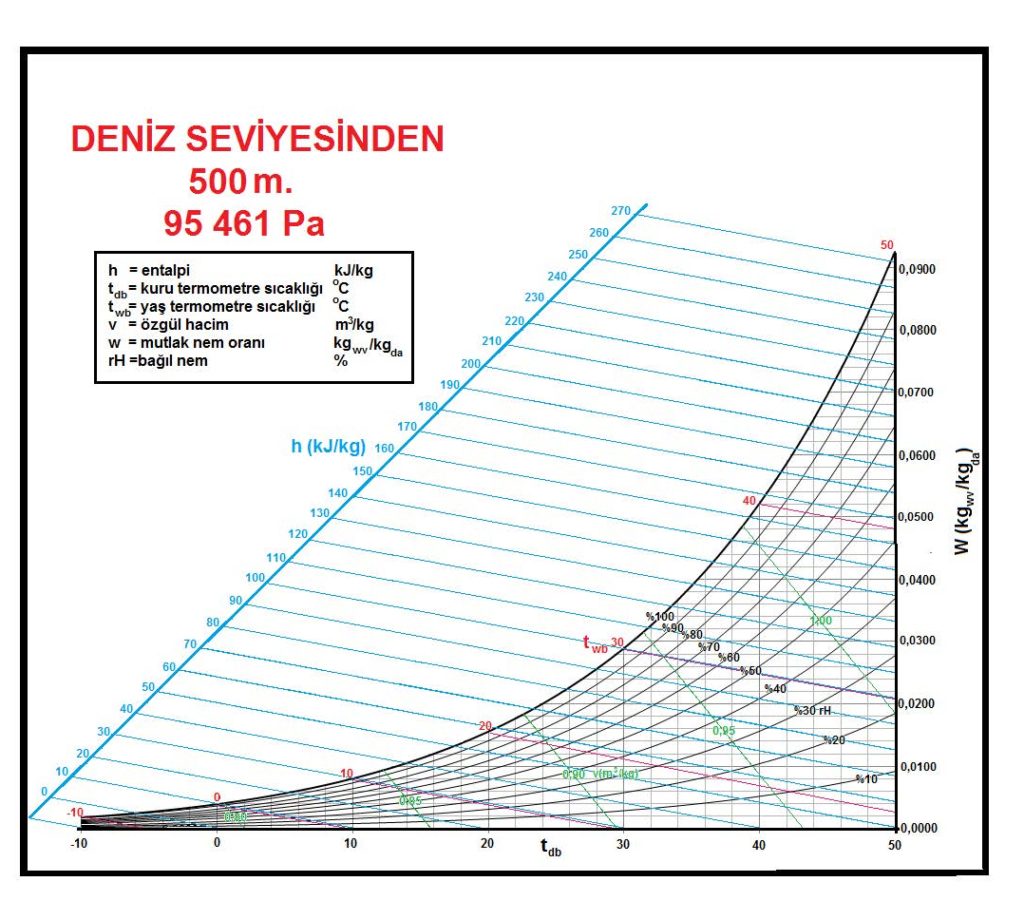
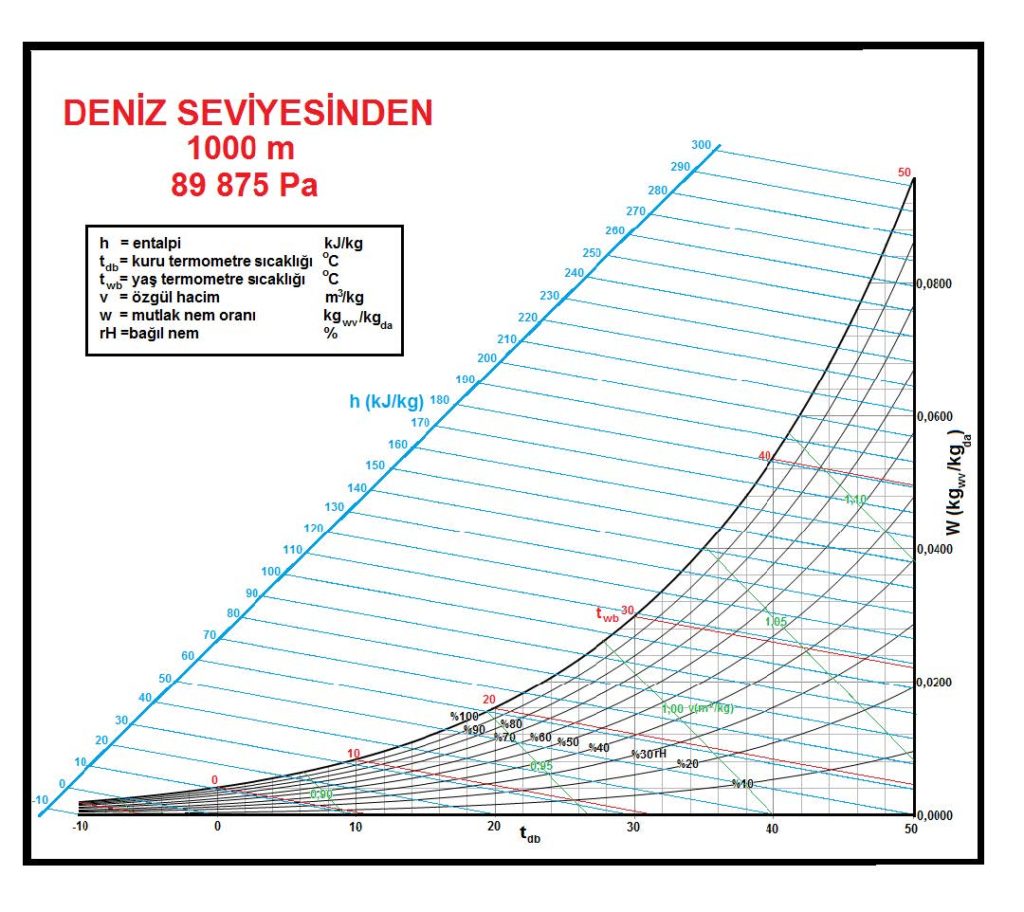
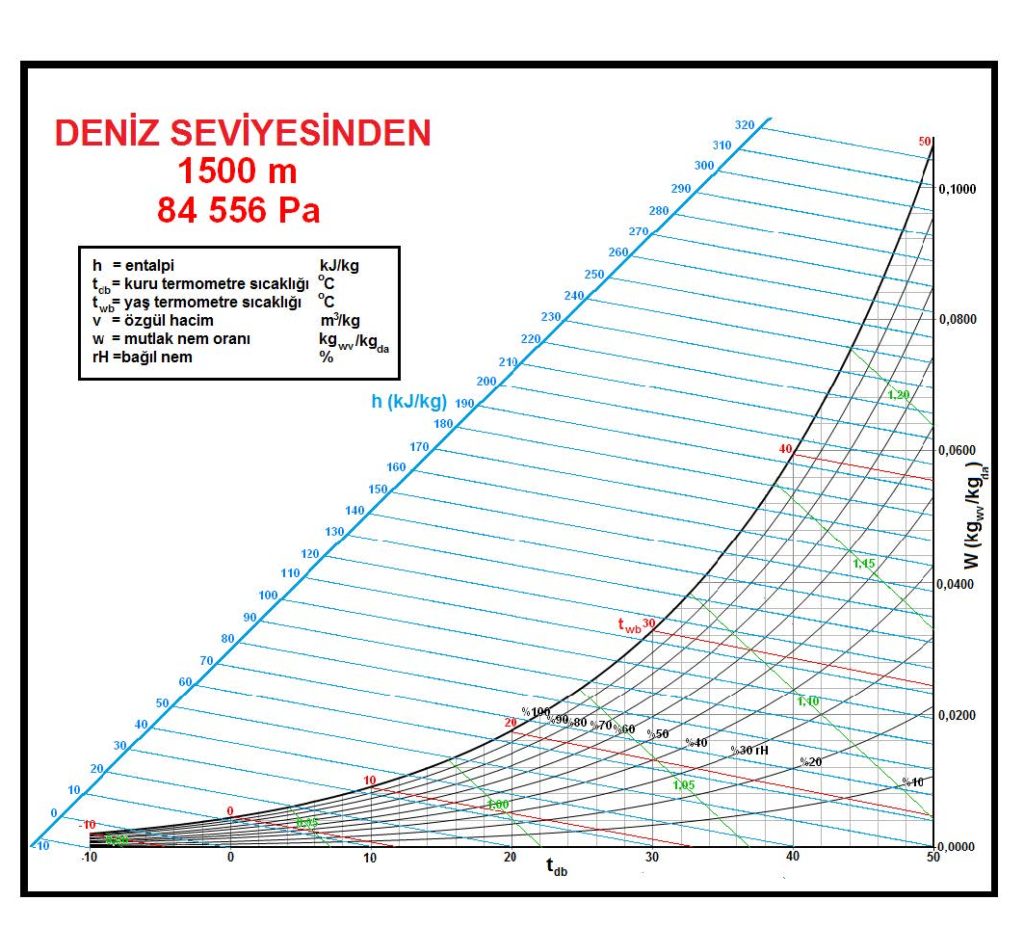
Bu durum karşımıza psikrometrik diyagramlarda üçüncü bir ekseni ortaya çıkarmaktadır. “Z” ekseni olarak adlandırabileceğimiz bu eksen deniz seviyesinden olan yüksekliktir. Aşağıdaki resimde 0 ve 1500m irtifalarda birçok değerin değişimi izlenmektedir.

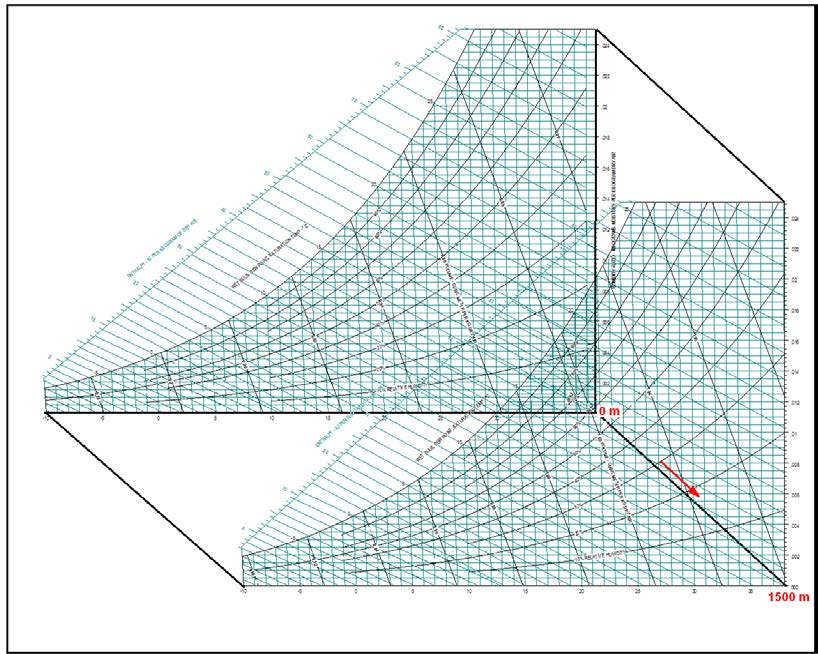
Örneğin kuru havanın özgül hacmi artmakta, kuru termometre sıcaklıklarının doyma noktalarındaki mutlak nem oranları da keza artmaktadır. Bunların yanı sıra özgül entalpilerde de farklılıklar meydana gelmektedir. Buradan da klima proseslerinin en doğru ve/veya irtifa açısından en yakın psikrometrik diyagramlara işlenmesi, örneğin ısıtma-soğutma yükleri, nemlendirme miktarı, nem alma işlemi için gereken soğutma yüklerinin bu diyagramlarda belirlenmesi şarttır. Aksi halde diyagram üzerinden yapılacak hesaplamalar belirli hata oranlarına sahip olacaktır.

4.2. DENİZ SEVİYESİ PSİKROMETRİK DİYAGRAMLARI

4.2.1. Normal Sıcaklık Psikrometrik Diyagramı

-10^OC ila +50^oC arasındaki sıcaklıklara hitap eden, İMEKSAN A.Ş.’nin kullandığı psikrometrik diyagramı burada sunuyoruz. Çünkü bu sayede dış hava sıcaklığı 0^oC’ın altında olan yerlerde de ısıtma yüklerini diyagram üzerinde belirlemek mümkün olmaktadır. Ayrıyeten bu diyagramda buhar basınçları da kırmızı bir koordinat  ile gösterilmektedir.

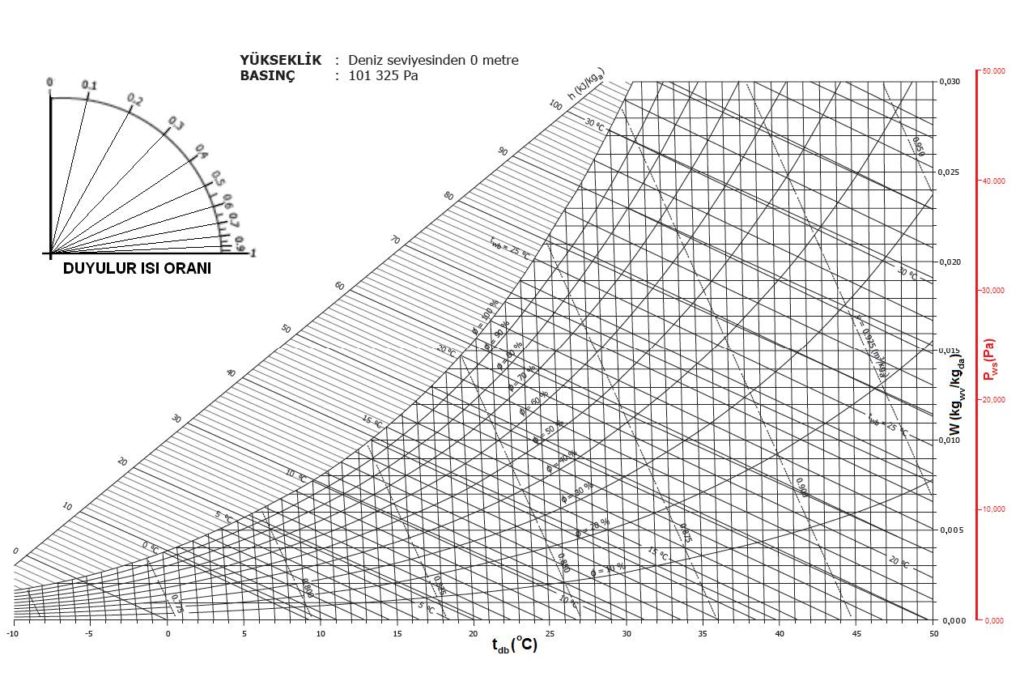
4.2.2. Düşük Sıcaklık Psikrometrik Diyagramı

  

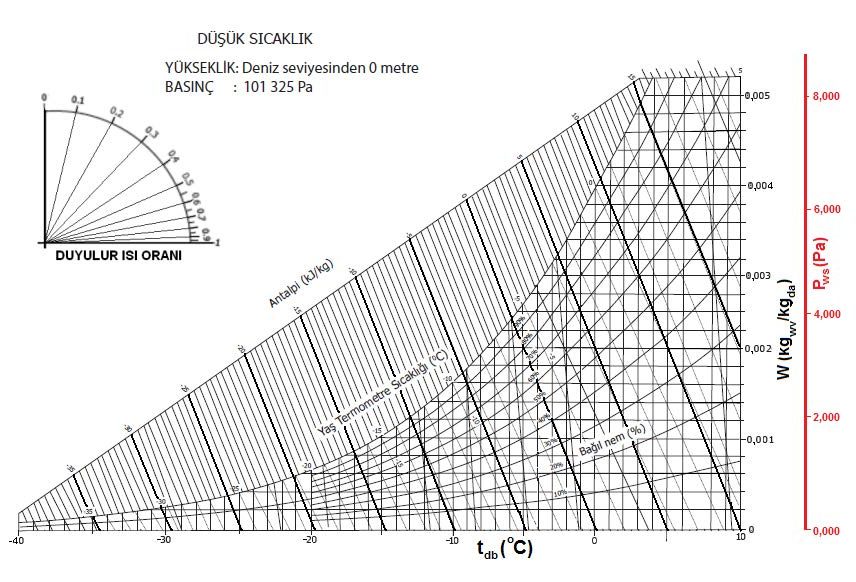
4.2.3. Yüksek Sıcaklık Psikrometrik Diyagramı

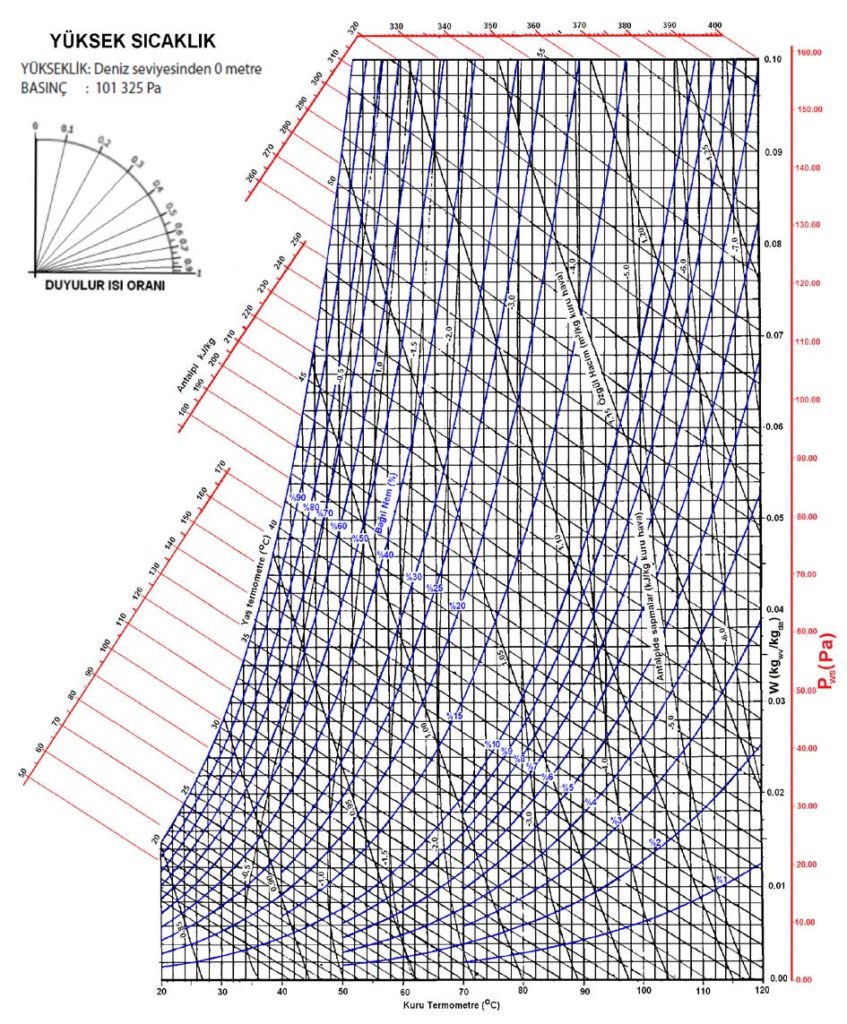
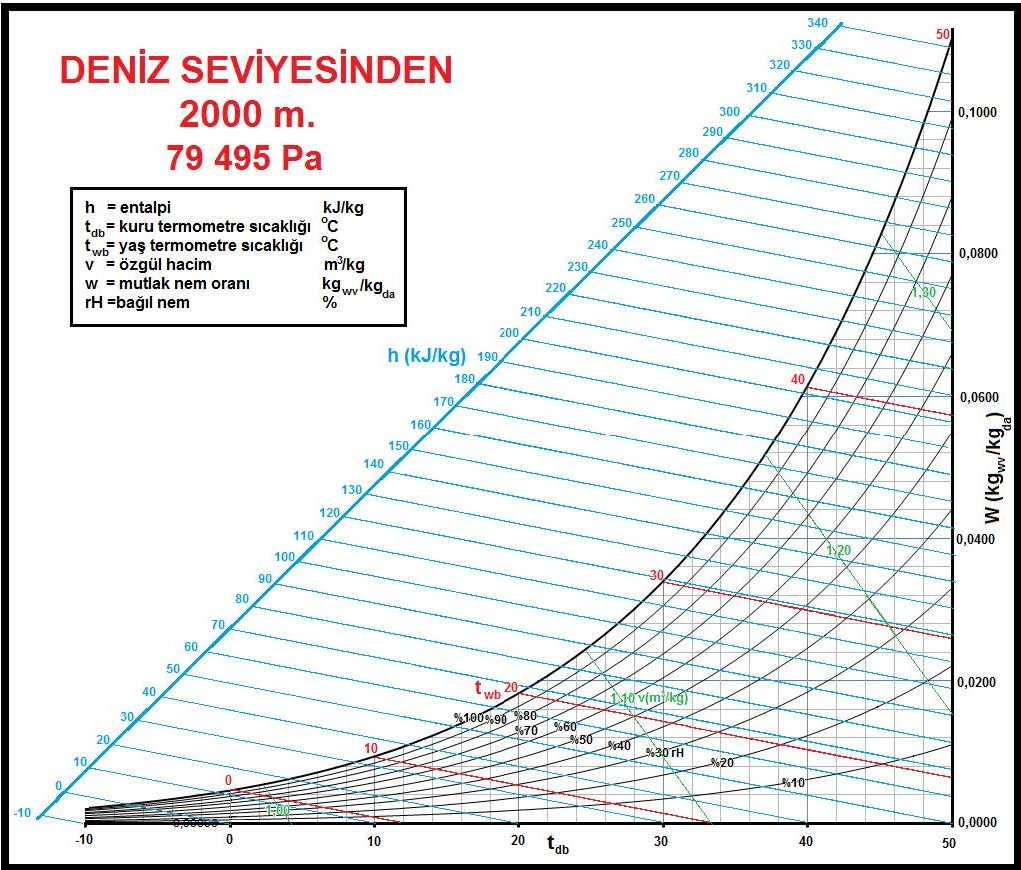
4.3. DENİZ SEVİYESİNDEN YÜKSEK MAHALLER İÇİN PSİKROMETRİK DİYAGRAMLAR

4.3.1. Genel

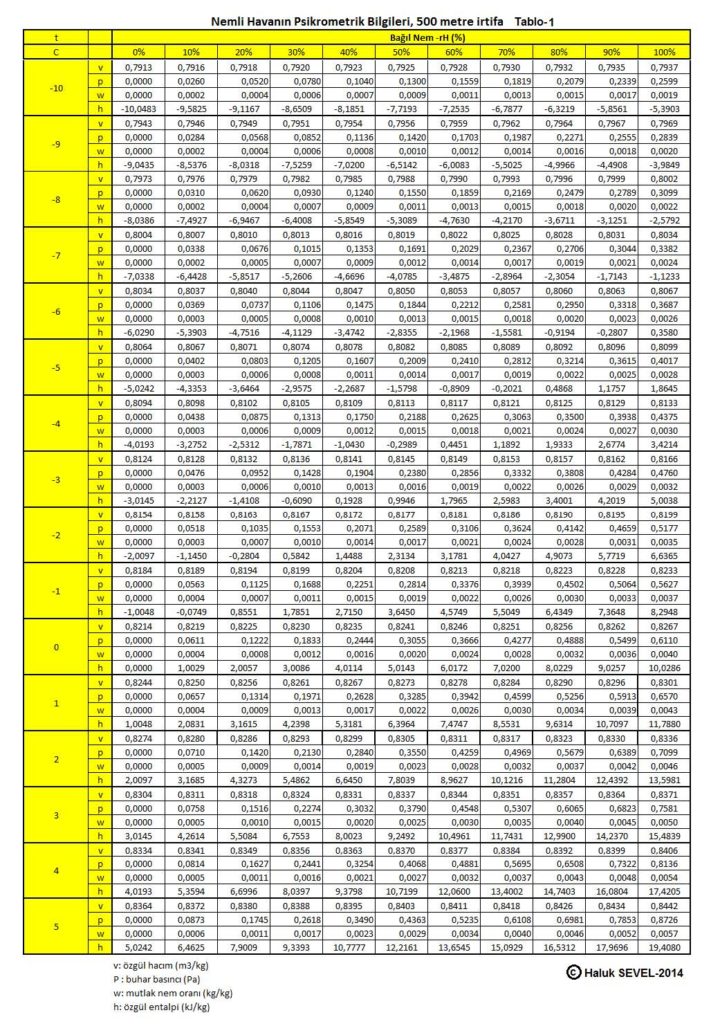
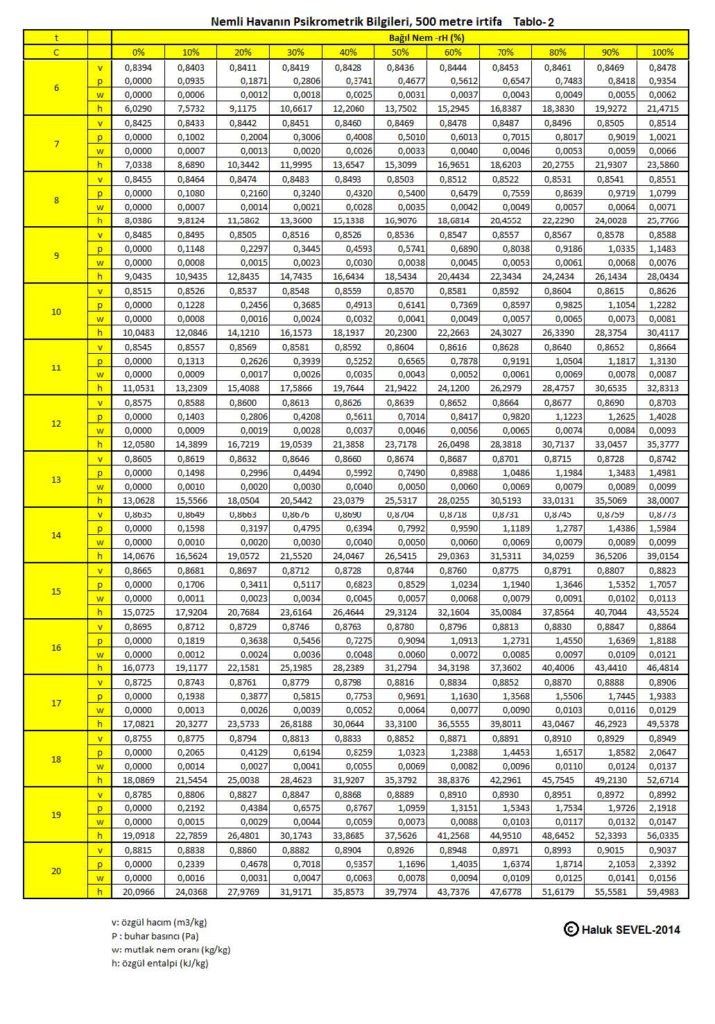
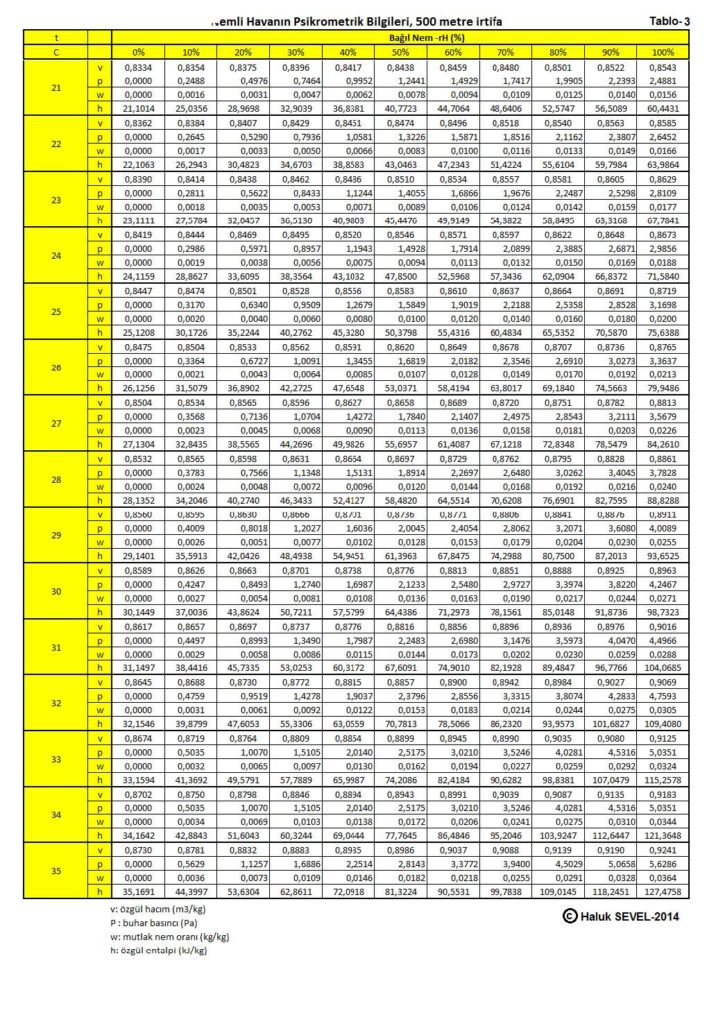
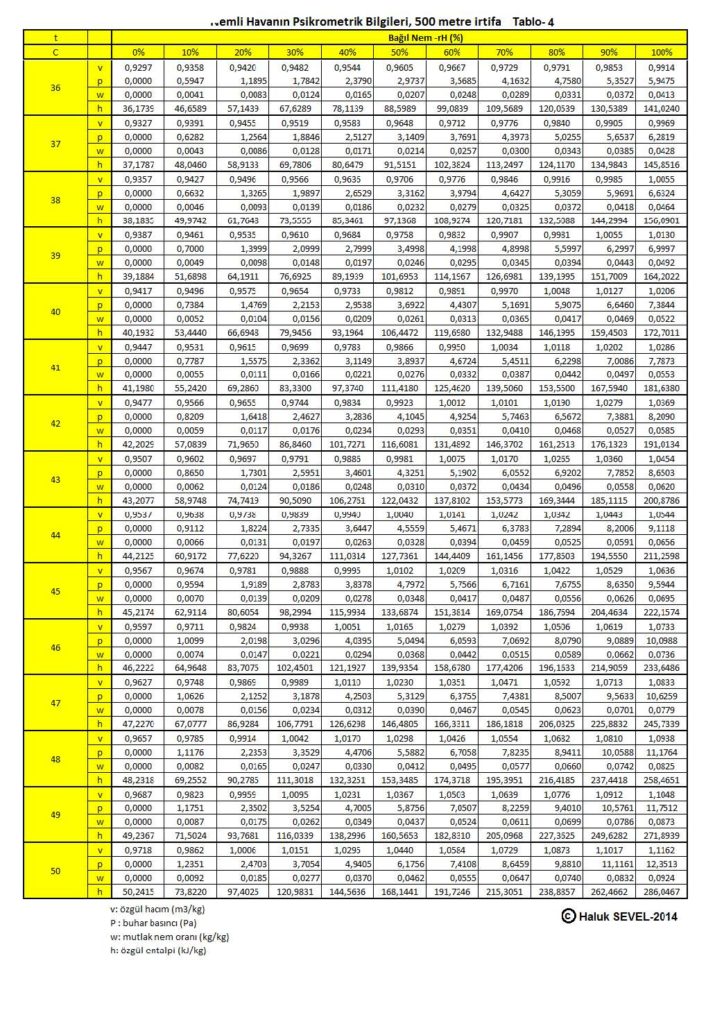
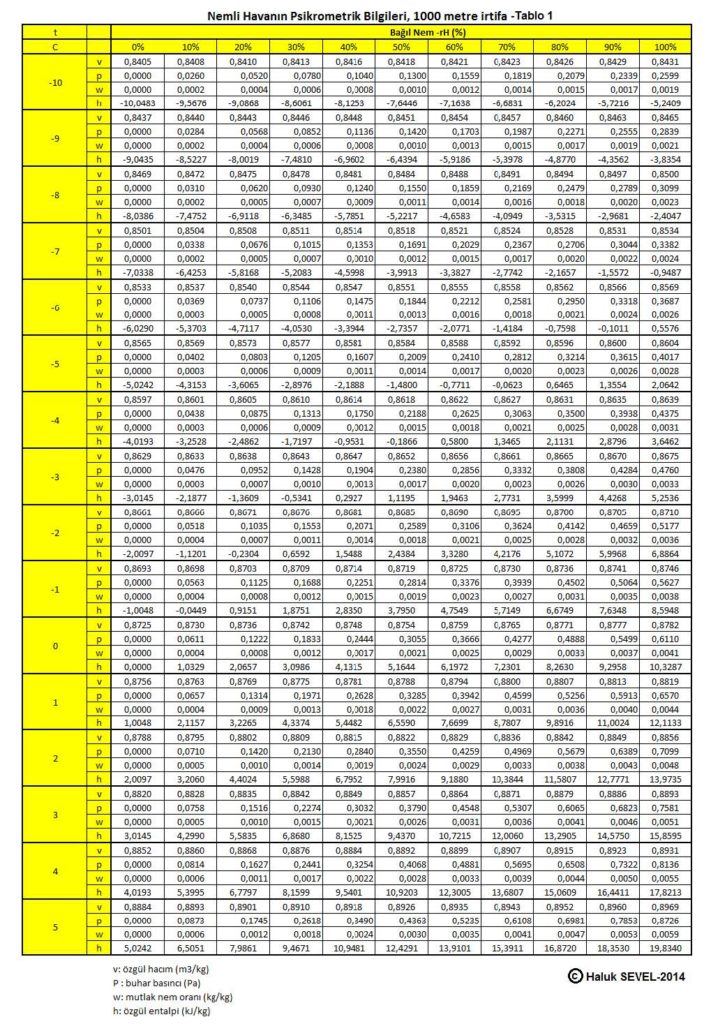
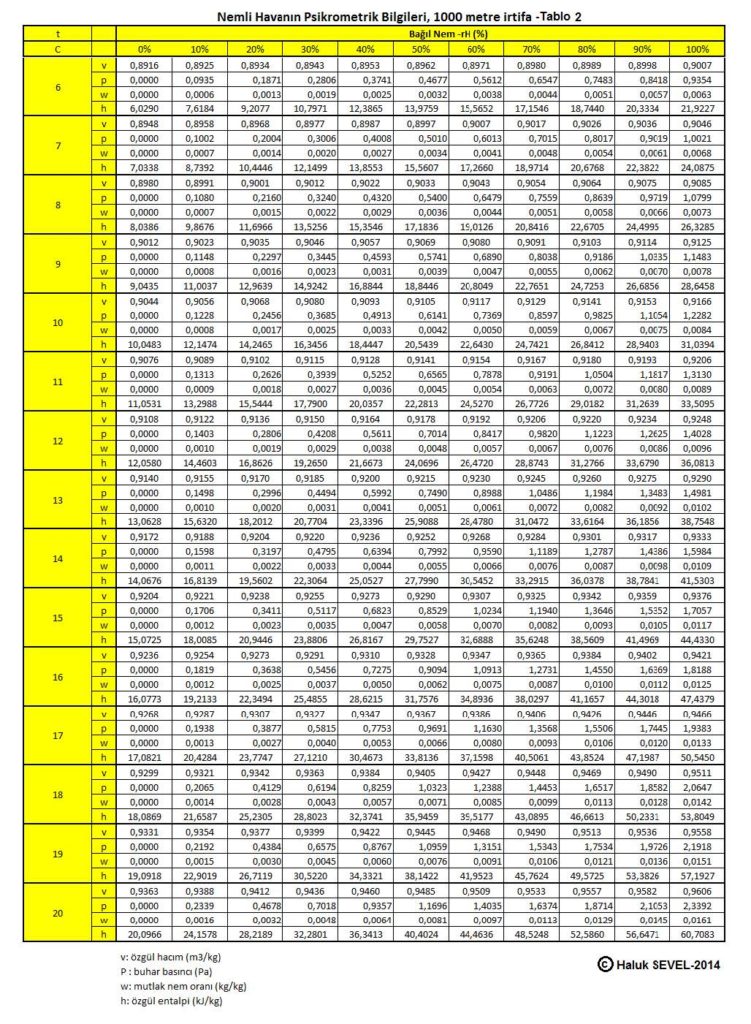
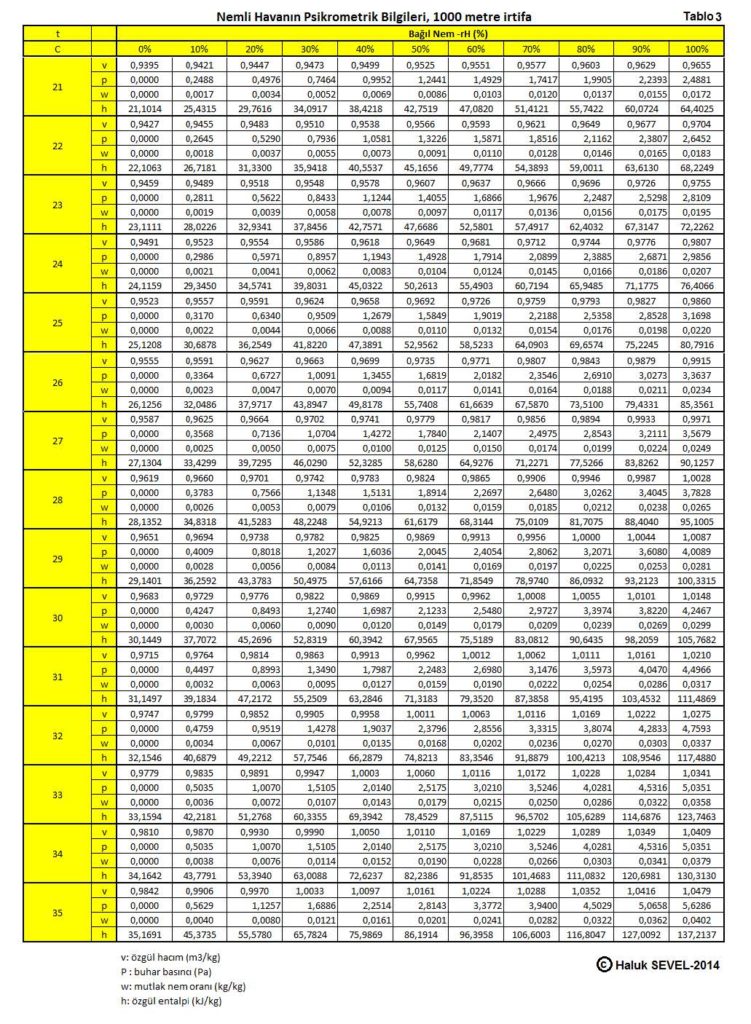
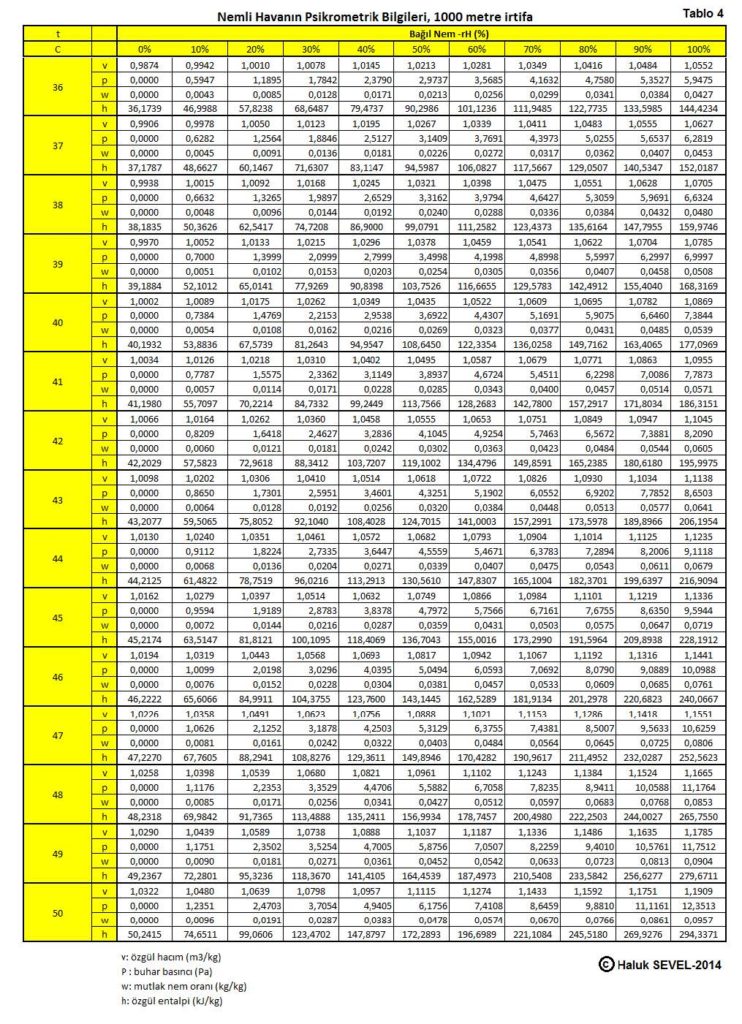
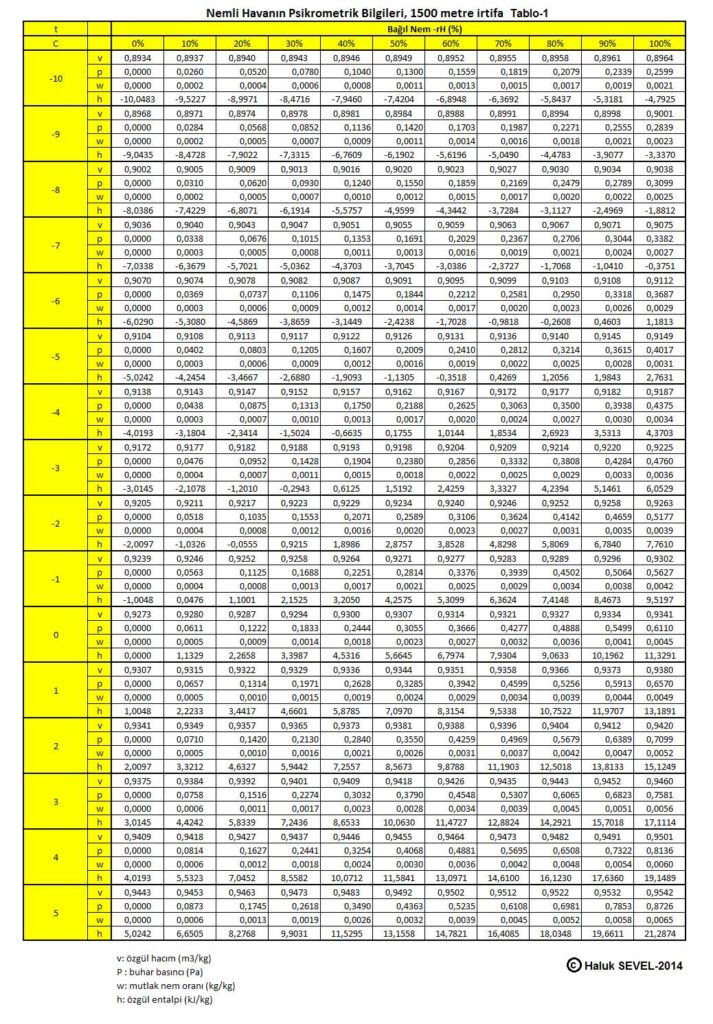
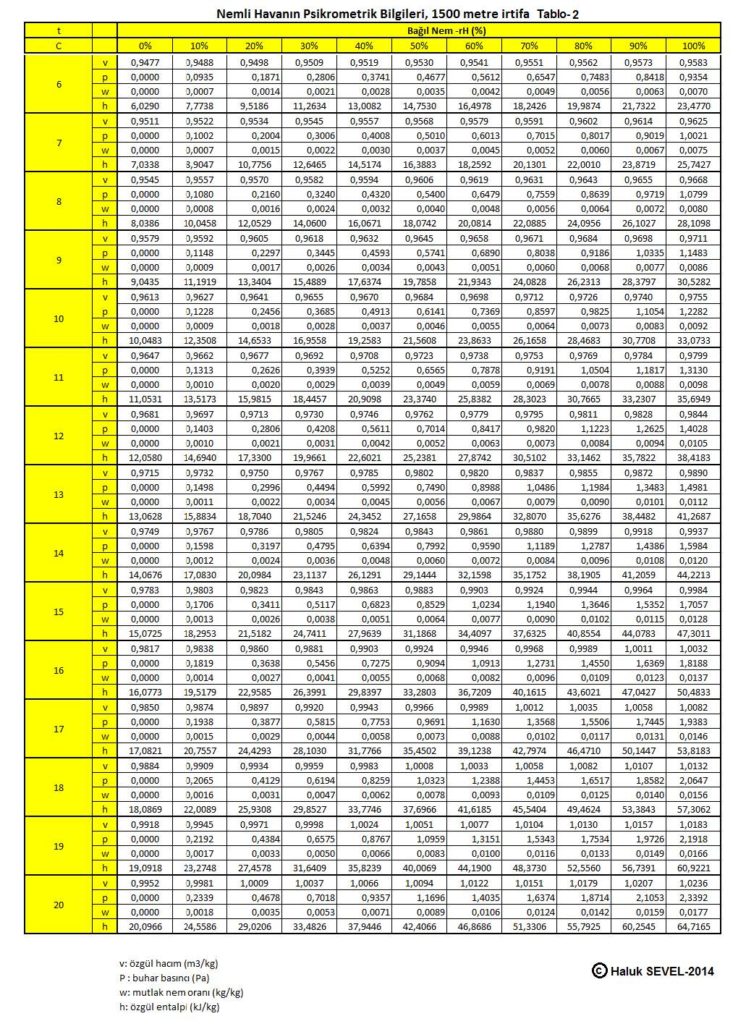
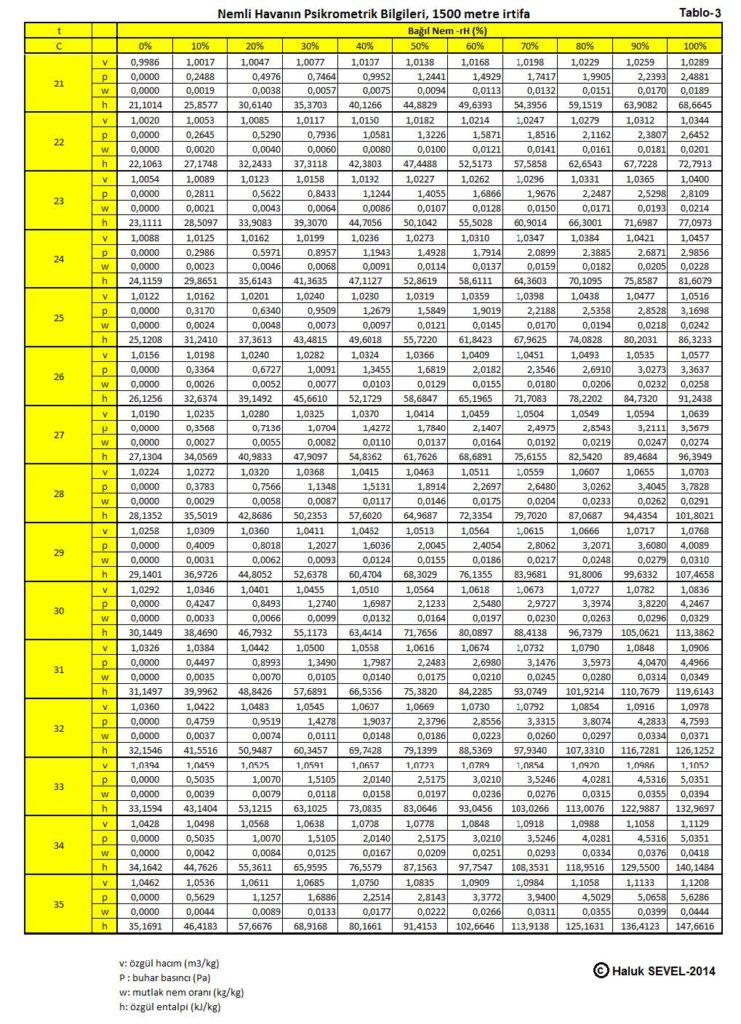
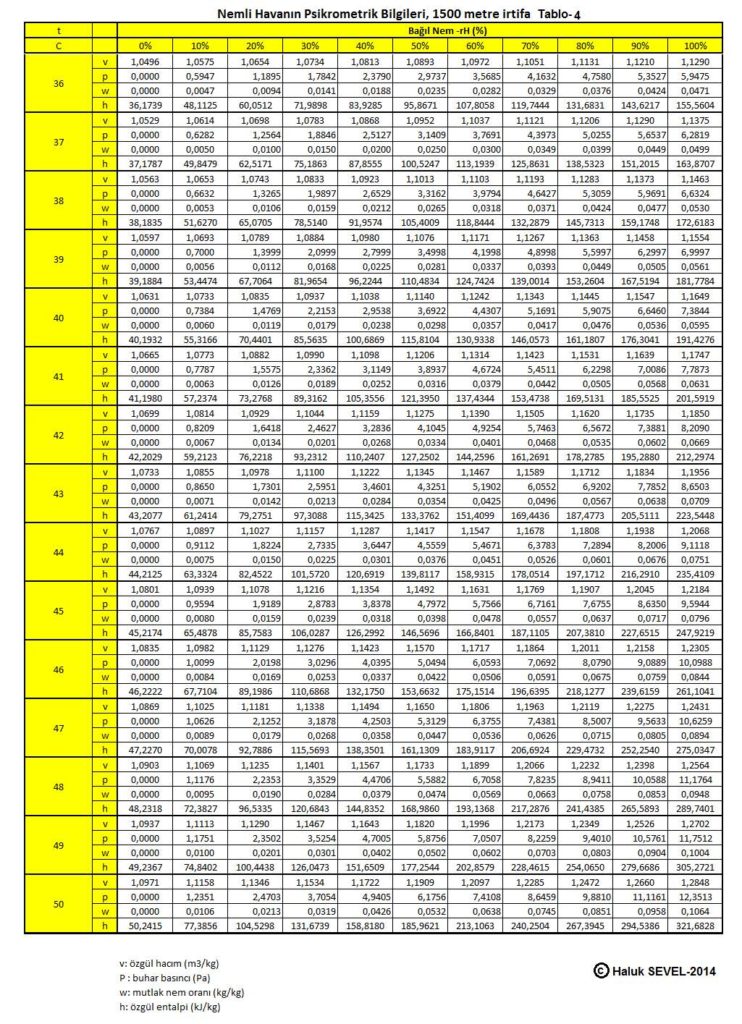
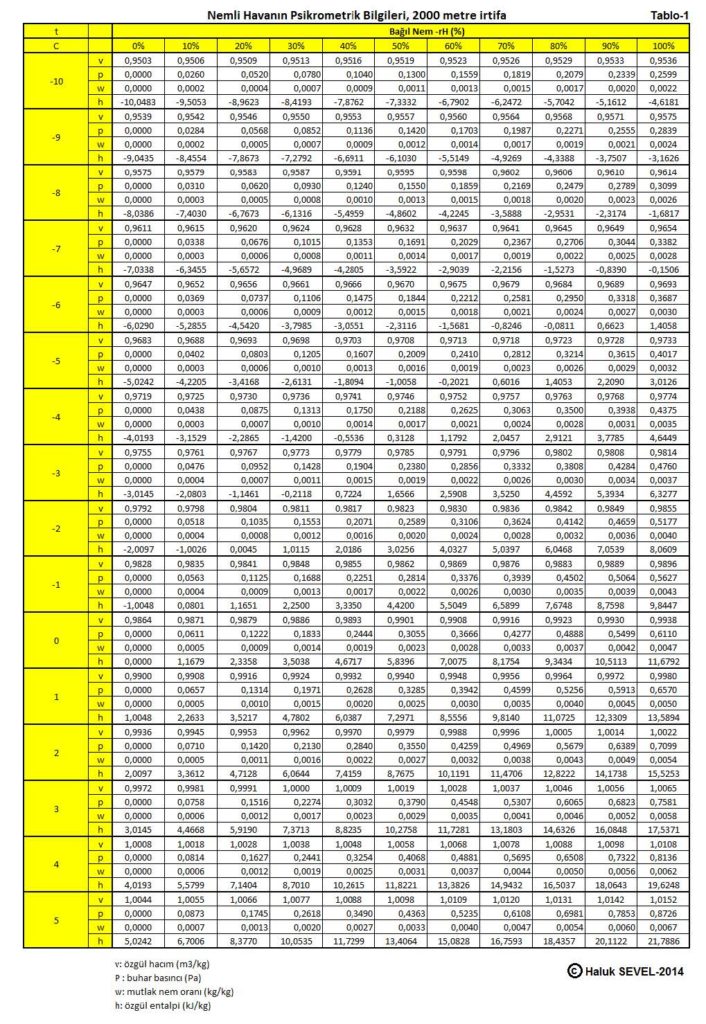
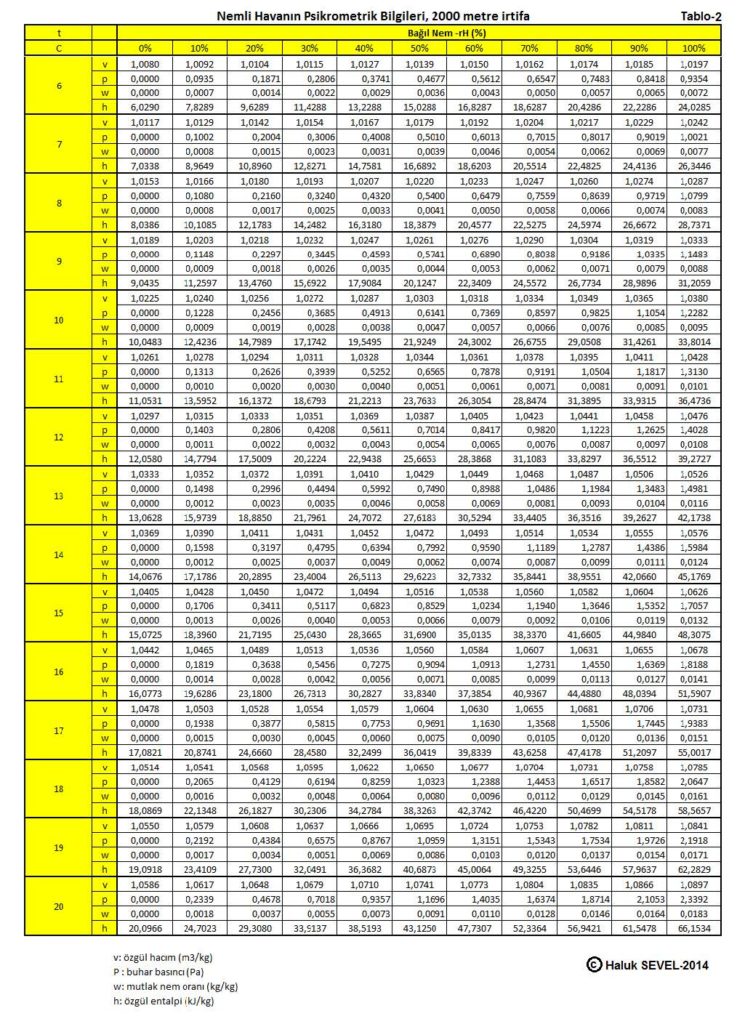
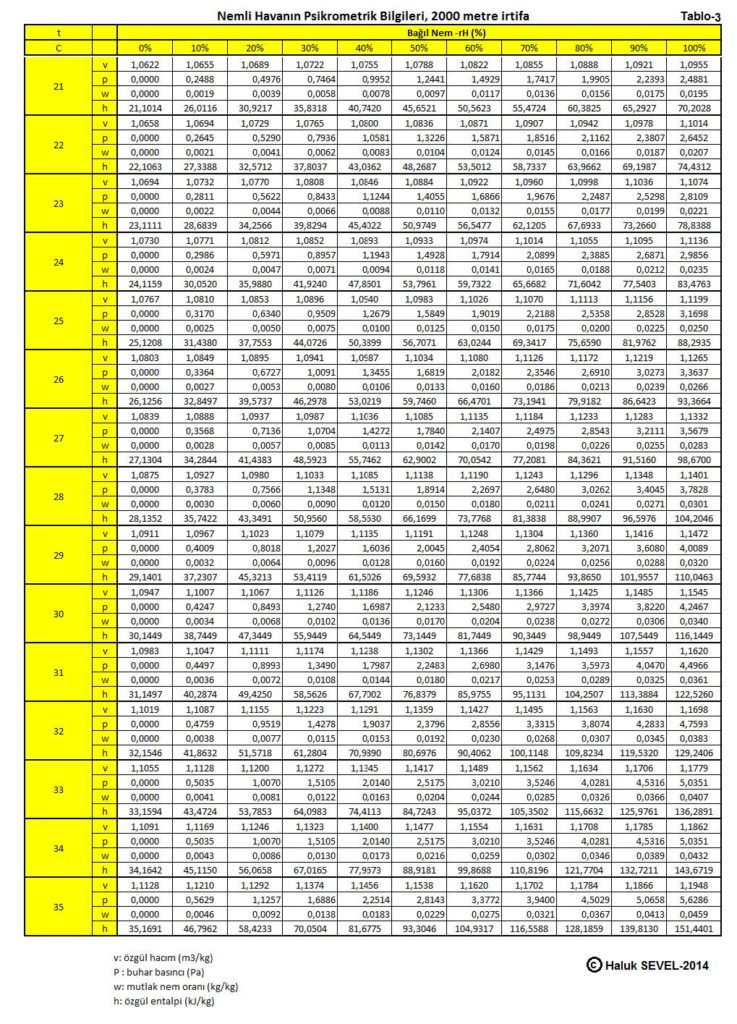
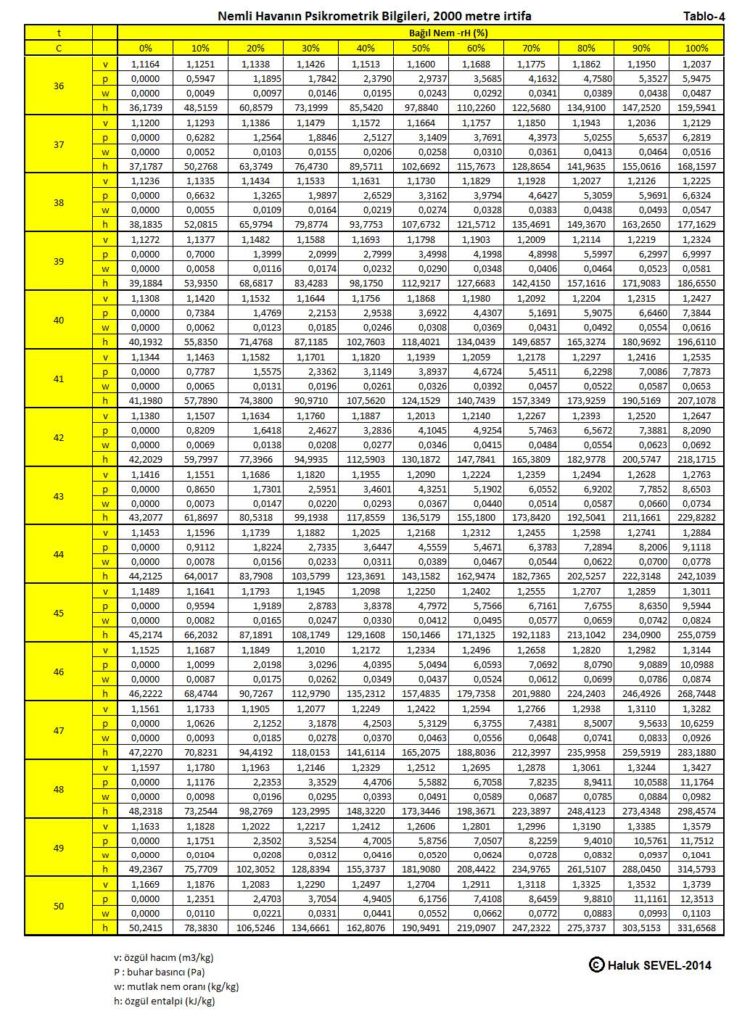
ASHRAE’in  geliştirdiği psikrometrik diyagramlar arasında üç tane de yüksek irtifalar için psikrometrik diyagramlar bulunmaktadır. Bu diyagramlar 750 metre, 1500 metre ve 2250 metre içindir. Ancak ülkemiz dikkate alındığında bu diyagramların 500 metre, 1000 metre, 1500 metre ve 2000 metre irtifalar için yapılmasında büyük faydalar vardır.

İrtifaya bağlı değişkenler içinde başta barometrik basınç gelmektedir. Barometrik basınç deniz seviyesinden olan yükseklik arttıkça, buna bağlı olarak düşüş göstermektedir. Bu değişikilk 2.4.1’deki tabloda gösterilmiştir. Aynı tabloyu burada bir daha veriyoruz.

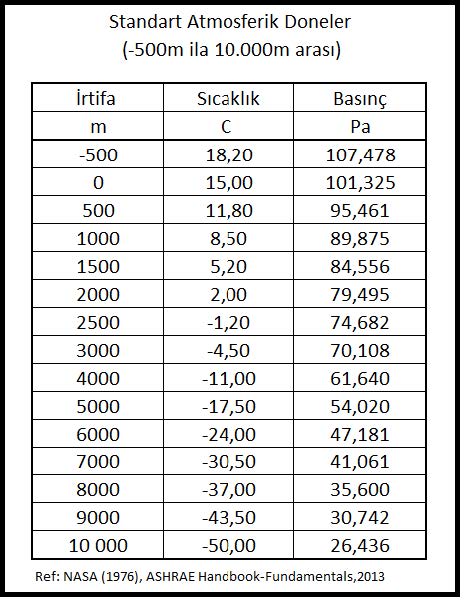
Yukarıdaki tablodaki atmosferik basınç değerleri , aşağıdaki formülle hesaplanmıştır.

P_bar=101,325 (1- 2,25577 x 10^-5 x Z)^5,2559

                                Z=Deniz seviyesinden irtifa (m)

Buhar basıncı da 3.9’da aşağıdaki gibi ifade edilmişti.

P_wv=1.6077W(101.325(1 – 2.25577 x 10^-5x Z )^5.2559-P_wv)

Bu formüllerden hareketle psikrometrik diyagramı oluşturabilmemiz için gerekli doneleri aşağıdaki gibi formülize edebiliriz:

Mutlak nem oranı: ( bkz.konu 3.8 )

W=0.622P_wv/(P_bar-P_wv)…………………………………………. (g/kg)

 Özgül hacım:

γ= V/m_a=(R_a.T)/(P_bar-P_wv) =(R_a.T)/(1+ w/622).(m³/kg)

 Özgül Entalpi:

h= h_da+ W.h_wv=1,005t + W(2,501 + 0,001805 x t )..(kJ/kg)

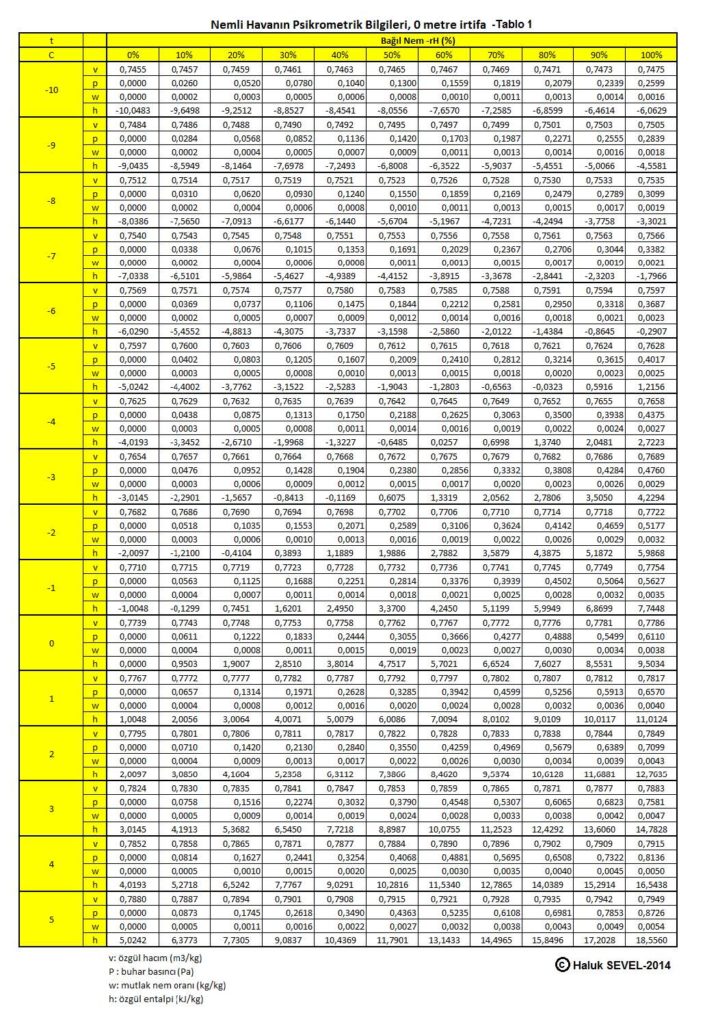
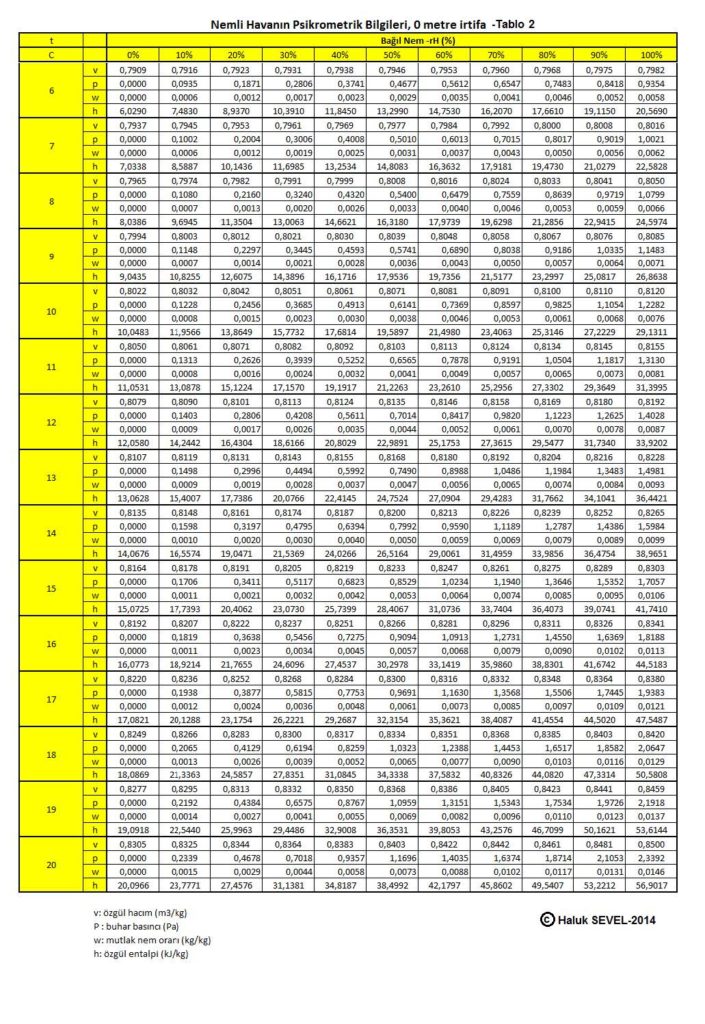
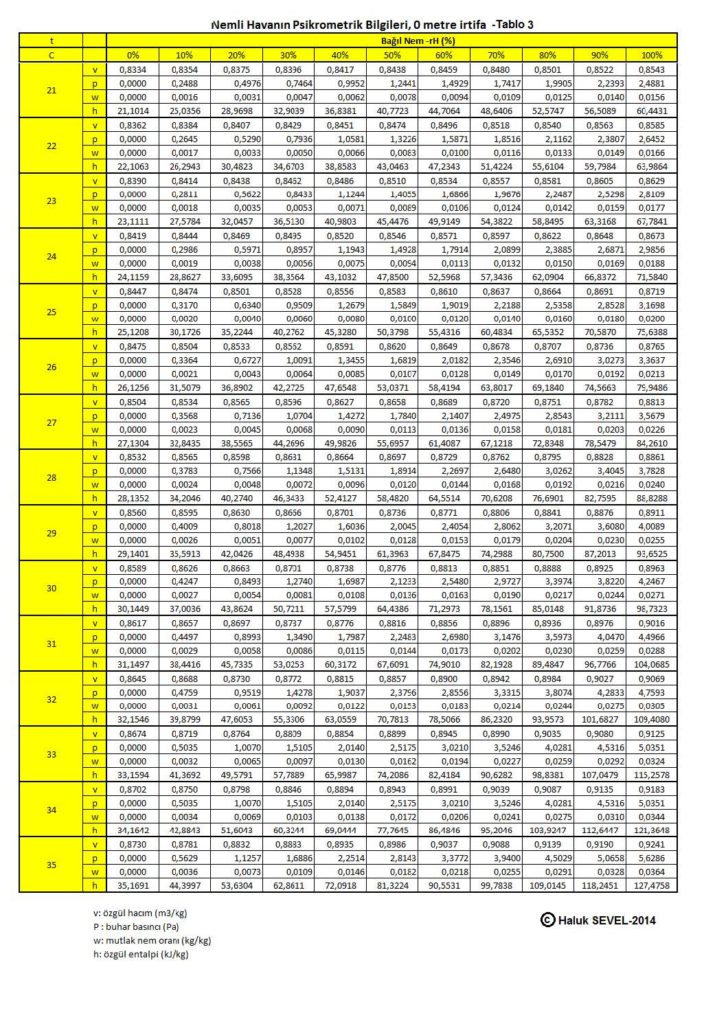
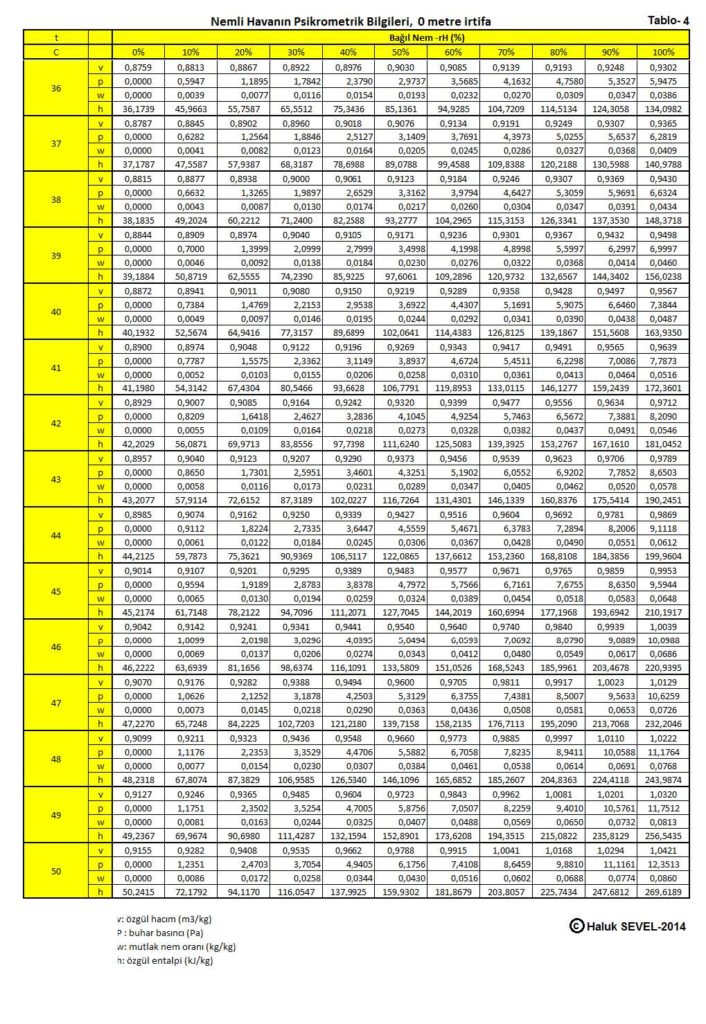
 Bu formüller esas alınarak hesaplanmış olan 0, 500, 1000, 1500 ve 2000 metre irtifaların psikrometrik tabloları  üçüncü bölüm, konu-8 “Tablolar”da verilmektedir.  Ayrıca ASHRAE psikrometrik diyagramları esas alınarak geliştirilmiş 750m, 1500m ve 2250m irtifalara ait psikrometrik diyagramlar da aşağıda gösterilmektedir.

4. PSİKROMETRİK ÖZELLİKLER VE TERİMLER

3.1. Giriş

Üç temel piziki öge belirlendiği ve sabit olduğu sürece kuru hava ile su buharının karışımı sabittir ve değişemez. Bu ögeler şunlardır:

a) Barometrik basınç (veya irtifa)…………………………..( P_atm)
b) Kuru termometre sıcaklığı………………………………….( t_db)
c) Aşağıdaki üç değişkenden herhangi biri

• Yaş termometre sıcaklığı veya…………………( t_wb )
• Bağıl nem veya………………………………………(rH )
• Çiy noktası………………………………………………( t_dp)

“c” şıkkındaki üç unsur birbirine bağlı olduğu için “a”,”b” deki ögelerle “c” deki ögelerden birinin belli ve sabit olması  kuru hava ile su buharı karışımının durumunu da belirler ve sabitler. Bu husus aynı zamanda “c” şıkkındaki diğer iki değişkeni de belirler ve sabitler. Bu özellikler aşağıdaki psikrometrik diyagramda gösterilmiştir.

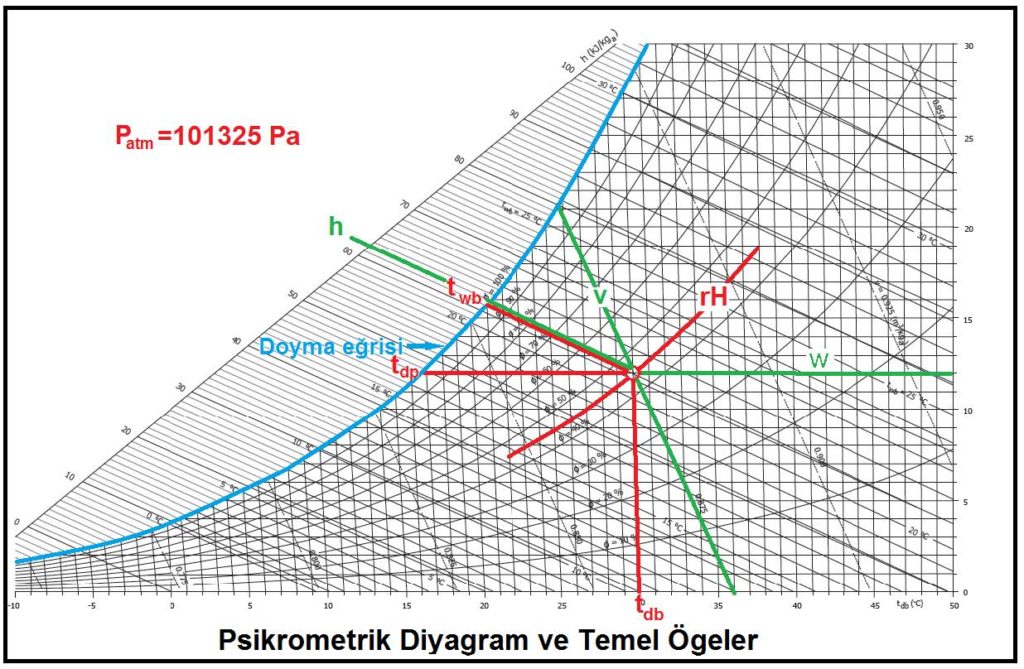
Bu diyagramda temel psikrometrik konumu belirleyen ögeler kırmızı renkte gösterilmiştir. Bu ögelerin yardımıyla diğer önemli üç doneyi de psikrometrik diyagramdan okumak mümkündür. Bu doneler şunlardır:

• Entalpi ……………………………………………………( h)
• Mutlak nem…………………………………………….(w )
• Özgül hacım……………………………………………( v )

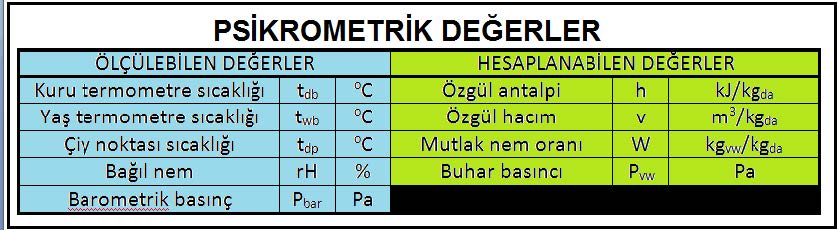
Bu sayede dokuz temel nokta belirlenmiş olmaktadır. Bu noktalardan beşine ölçülebilen değerler, diğer dördüne de hesaplanabilen değerler diyebiliriz. Bu husus aşağıdaki tabloda özet olarak gösterilmektedir.

 3.2. Kuru Termometre Sıcaklığı

Kuru termometre sıcaklığı herhangi bir alkollü ve civalı termometre ile veya aynı değerlere kalibre edilmiş hissedici+transduser ile ölçülen mahal veya çevre sıcaklığıdır. Bu sıcaklık “t_db” sembolü ile gösterilir. Birimi ise “^oC”veya “K”dir. Daha önceki bahislerde anlatıldığı gibi “^oC” Celsiyus skalası olup bu skalada 0^oC deniz seviyesinde suyun donma sıcaklığına, 100^oC ta deniz seviyesinde suyun kaynama noktasına tekabül etmektedir. “K” ile gösteriklen Kelvin ölçeği ise mutlak sıfırı esas almıştır, bu sıcaklık Selsiyus skalasında -273.15^oC’a eşittir.

Kuru termometre sıcaklığı psikrometrik diyagramda “^oC” olarak diyagramın altında , absisinde yer alır ve düşey hatlar ile gösterilir.

Kuru termometre sıcaklığı gösteren absiste 0^oC kuru hava sıcaklığı aynı zamanda entalpik değerlerin başlangıç, yani referans noktası olarak kabul edilir ve bu noktadan itibaren kuru havanın entalpik değerleri hesaplanır. Bu hesaplamayı aşağıdaki formüller ile gösterebiliriz.

Q=M. C_p-da(t_2db-t₀)

Bu denklemde “t₀” havanın entalpik hesaplamada referans noktası olan  0^oC sıcaklığı, “t₂”iseentalpisinin ölçülmesi istenen kuru havanın sıcaklığını göstermektedir. “C_p-da” değeri ise havanın özgül ısısıdır; birimi “kJ/kg”dır.

C_p-dakuru havanın özgül ısısıdır. Özgül ısı bir kilogram ağırlığındaki bir nesnenin ısısını 1^oC arttırmak için gerekli olan ısıdır. Bu değer 15^oC’taki bir kilogram suyun ısısını bir derece arttırmak için gerekli olan ısıya orantılı olarak belirlenir. Bu değer kCal/h birimleriyle su için 1.00 kCal/kg, kuru hava için 0.24 kCal/kg’dır. Uluslararası kullanımda olan “SI” birimleriyle ifade edildiğinde kuru havanın özgül ısısı 1.00483 kJ/kg’dır. Su buharının özgül ısısı da 1.83’dür. Havanın özgül ısısı kuru termometre sıcaklığına bağlı olarak çok az değişiklik göstermektedir. 1.00483 kJ/kg değeri esas alındığında -10^oC ile +50^oC arasında yapılacak hesaplarda hata payı %0.2’den küçük olmaktadır. Aşağıdaki tabloda “C_p” değerindeki değişmeler gösterilmektedir.

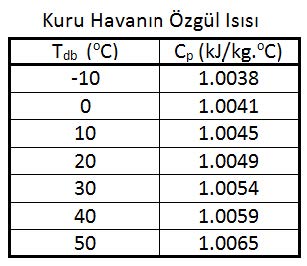
Aynı şekilde su buharının özgül ısısında da aynı sıcaklık aralığında çok küçük, kabili ihmal farklılıklar olmaktadır.

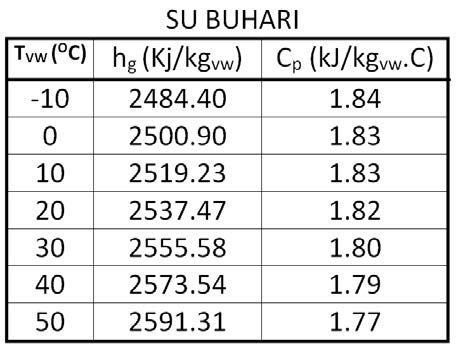
Dolayısıyla su buharının özgül ısısını 1.82 kJ/kg.C olarak kabul edebiliriz.

Bir önceki sayfadaki formülü birim kitle, 1 kg kuru hava için yaptığımızda kuru havanın “t₂” sıcaklığındaki antalpisini hesaplamış oluruz.

h_2da=C_p-da(t_2db-t₀)

Doymuş havanın entalpisini de kuru havanın entalpisi ile doyma noktasındaki mutlak nem oranının buharın özgül ısının çarpımının toplamı olarak bulabiliriz.

h_2sa=C_p-da(t_2db-t₀) + C_p-vw.W(t_2db-t_o)

 h_2sa=t_2-da(C_p-da+ C_p-vw.W)  …………………………(kJ/kg)

3.3. Yaş Termometre Sıcaklığı ve Adyabatik Doyma

Yaş termometre ile ilgili birçok tarif vardır. Bunlardan biri yaş termometre sıcaklığını “buharlaşma sıcaklığı” olarak, diğer bir tarif  te  “%100 doyma noktasına gelinmesi ile neticelenen evaporatif soğutma neticesi elde edilebilen en düşük sıcaklık” olarak tarif eder.  Termodinamik yaş termometre sıcaklığına aynı zamanda adyabatik doyma sıcaklığı da denmektedir.

Yaş termometre sıcaklığı “termodinamik yaş termometre sıcaklığı” ve “psikrometrik yaş termometre sıcaklığı”olarak ta tarif edilmektedir. Termodinamik yaş termometre sıcaklığı suyun buharlaşması ile havanın adyabatik olarak soğuması sonucu elde edilebilen en düşük sıcaklıktır. Sıvı haldeki su doymamış hava ile temas ettiğinde kısmi buhar basıncı farkı nedeniyle buharlaşır (bu konu ileriki bahislerde detaylı bir biçimde incelenecektir) . Bu buharlaşma işlemi adyabatik bir prosestir. Çünkü dışarısıyla hiçbir ısı alış-verişi yoktur. Buharlaşma için gerekli ısı havadan temin edilir ve bunun neticesi olarak hava soğur ama içindeki mutlak nem oranı artar. Neticede hava-buhar karışımının antalpik değeri sabit kalır.

Termodinamik yaş termometre sıcaklığı adyabatik doyurucudaki kitle ve enerji balansları dikkate alınarak ölçülür. Bu nedenle termodinamik yaş termometre sıcaklığına adyabatik doyma sıcaklığıda denir.  Adyabatik doyurucu olarak adlandırılan enstruman aslında teoretik bir enstruman olup mutlak izolasyona sahip olması ve çok uzun (sonsuza yakın) bir boyda olması gerekir.

Mollier Diyagramı’nda ve 1963’den itibaren ASHRAE’in Psikrometrik Diyagramları’nda izometrik çizgiler halinde gösterilen yaş termometre sıcaklığı çizgileri bu ölçme tekniği ile belirlenen termodinamik veriler esas alınarak tanzim edilmiştir. Aşağıdaki resimde adyabatik doyurucunun şematik bir çizimi yer almaktadır.

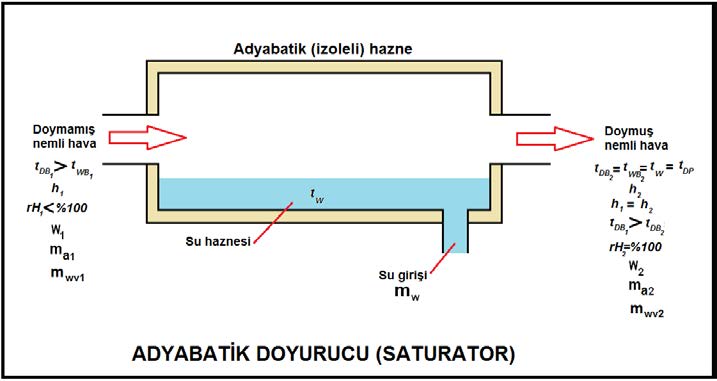
Kuru hava ve su buharı karışımı ile belirlenen psikrometrik yaş termometre sıcaklığı klasik bir termometrenin, örneğin cıva veya alkollü cam termometrenin hissedici ucunun yumuşak ve temiz bir pamuk sarılması, pamuğun iyice ıslatıldıktan sonra 3 ila 5 m/s hava hızına tabi tutulması ile ölçülür. Islatılmış uç üzerinden geçen hava akımı suyun buharlaşmasına ve termometrede gösterilen sıcaklığın düşmesine neden olacaktır. Bir müddet sonra ölçme kararlı rejime giriiecek, termometrede görünen değer sabitlenecektir. Bu değer psikrometrik yaş termometre sıcaklığıdır. Bu ölçme işlemi esnasında termometrenin ve özellikle ucunun güneş radyasyonuna maruz bırakılmaması gerekir. Ölçme ucunu kaplayan pamuk devamlı ıslak tutulmalıdır. Bunun için pamuğun fitil tarzında uzatılması ve bir su haznesine batırılmış olması gerekir (bkz. Bölüm-1 HYDRODEIK). Benzer bir yaş termometre psikrometresi aşağıdaki resimde gösterilmektedir.

Kuru termometre ile yaş termometre sıcaklıkları rarsındaki farkın (t_db-t_wb) 10^oC’tan büyük olması  fitilin hareket halindeki hava ile teması esnasında ısınmasına ve bu ısının hazneye iletilerek suyun bir miktar ısınmasına neden olur. Böyle durumlarda ölçülen yaş termometre sıcaklıkları olması gereken değerlerden biraz yüksek çıkabilir.

Buradaki işlem adyabatik doyurucudaki işlemin birebir aynı değildir. Ancak psikrometrenin uygun bir yere yerleştirilmesi koşuluyla iki ölçüm arasındaki sapmalar ihmal edilebilecek minimum seviyelerde tutulabilir.

Adyabatik Doyurucu’da yapılan işlemi termodinamiğin iki temel kanununun ışığı altında inceleyebiliriz. Adyabatik doyurucuya giren kuru havanın debisi “m_a1”, çıkan havanın debisi de “m_a2” gösterilmektedir. Buharlaşan su miktarı da “m_w” dir. “w₁”ve “w₂” giriş ve çıkıştaki havanın içindeki mutlak nem oranını göstermektedir. Kitlenin korunumu kanununa göre denklemimizi kurarsak:

m_a1=m_a2=m_a……………………………..(kuru havanın debisi)

m_wv1+m_w=m_wv2…………………………..(havadaki buharın debisi)

Bu denklemi su buharı için aşağıdaki gibi de yazabiliriz.

m_a.w₁+ m_w= m_a.w₂

Böylece:

m_w=m_a(w₂-w₁)…………………………….. (buharlaşan suyun debisi)

Benzer denklemleri de enerjinin korunumu kanununa göre yazabiliriz.

∑m₁.h₁=∑m₂.h₂

Bu denklemde “m₁” girişteki doymamış nemli havanın kütlesini, “m₂”ise çıkıştaki doymuş nemli havanın kütlesini, “h₁” ve “h₂”ise aynı havaların giriş ve çıkıştaki antalpilerini, “h_wv1” ve “h_wv2”  su buharının giriş-çıkıştaki entalpilerini, “h_w”ise suyun entalpisini göstermektedir. göstermektedir. Buradaki eşitliğin nedeni prosesin adyabatik olmasından, dışarı ile herhangi bir enerji transferi olmamasından kaynaklanmaktadır.

Aynı denklemi şöyle de yazabiliriz:

m_a.h₁+ m_w.h_wv2 = m_a.h₂

m_a.h₁+ m_a(w₂-w₁).h_wv2 = m_a.h₂

Bu denklemi “m_a” kemiyetine böldüğümüzde aşağıdaki denklemi buluruz.

h₁+ (w₂-w₁).h_wv2 = h₂

(C_p.t_db1+ w₁.h_wv1)+(w₂-w₁)h_w2=(C_p.t_db2+w₂.h_vw2)

w₁=(C_p(t_dp1-t_dp2)+w₂.h_vw2)/(h_wv1-h_w2)……bulunur.

Daha önceki hesaplarımızda “m_wv/m_da”mutlak nem oranını aşağıdaki gibi hesaplamıştık:

m_wv/m_da=0.621945. P_wvs/(P- P_wvs) 

m_wv2/m_da=w₂ olduğuna göre yukarıdaki denklemde “w₁”değerini yerine koyduğumuzda “w₁” değerini de hesap yoluyla bulmuş oluruz.

Yaş termometre sıcaklıkları ASHRAE’in psikrometrik diyagramlarında ve Mollier’in i-x diyagramında birbirine paralel eğimli düz çizgiler olarak gösterilir. Bu çizgiler sabit antalpi çizgilerine de paraleldir.

• Çiy Noktası ve Çiy Noktası Sıcaklığı

Çiy noktası sıcaklığını satıh kondansasyonunun oluşmaya başladığı sıcaklık olarak tarif edebiliriz. Benzeri bir tarif ile, çiy noktasını havanın doyma noktasına eriştiği, daha fazla buhar kabul edemeyeceği sıcaklık olarak ta tanımlayabiliriz. Eğer buhar ilave edilmeye devam edilirse sis, satıh yoğuşması veya bulutlar oluşmaya başlar.

Çiy noktasının daha ilmi bir tarifi de yoğuşabilir herhangi bir buharın sabit basınçta yoğuşma başlamadan önce erişebileceği sıcaklıktır. Dolayısıyla doyma sıcaklığı ile çiy noktası sıcaklığı birbirine eşit anlamdaki tabirlerdir.

Çiy noktası sıcaklığını  basit bir deneyle kendimiz de yapabiliriz.

Bir bardağın içine oda sıcaklığında su kouyn. İçine de bir termometre daldırın. Bardağın içine azar azar buz ilave edip termometredeki düşmeyi izleyin. Bir süre sonra bardağın dış sathında su zerrecikleri belirmeye başlayacaktır. Bu zerrecikler yoğuşan havadaki su buharıdır. Yoğuşmanın başladığı andaki sıcaklık değeri de odanızın çiy noktasıdır.

Herhangi bir kuru termometre ve yaş termometre sıcaklıkları ile belirlenen ortam soğutulmaya başlandığında önce duyulur soğutma işlemi gerçekleşir (Bkz. Bölüm-5, konu 5.4.1 ve 5.4.2). Belirli bir sıcaklığa gelindikten sonra mahal havasının içindeki buhar da yoğuşmaya başlar ve bu noktadan itibaren duyulur ve gizli soğutma işlemleri beraber devam eder.

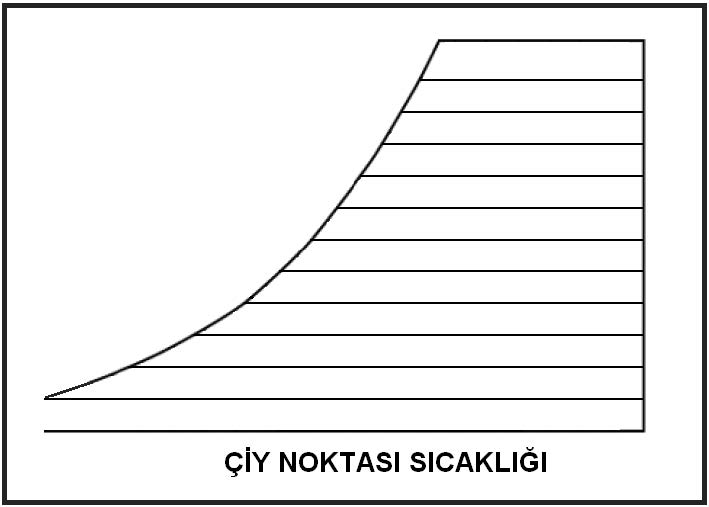
Çiy noktası mahal şartlarından kuru termometreyi belirleyen absise paralel bir çizginin çizilmesi ile bulunur. Bu çizginin doyma eğrisini kestiği nokta o ortamın çiy noktası sıcaklığıdır. Bu sıcaklık doyma noktası sıcaklığına eşittir.

Aynı zamanda bu noktanın kuru termometre ve yaş termometre sıcaklıkları da eşittir.

3.5. Bağıl Nem

-40^oC ila +65^oC arasındaki sıcaklıklarda yapılan deneyler su buharının ideal gaz karakteristiklerine sahip olduğunu göstermiştir. Bu görüş açısından hareketle bağıl nemi ortam şartlarında mevcut mutlak nem oranının aynı kuru termometre sıcaklığındaki mutlak nem oranına oranı olarak ifade edebiliriz. Bağıl nem için kulanılan simge “rH” olup “%” olarak ifade edilmektedir ve birimsiz bir kemiyettir.

rH (%)= (W_t1/Wdp._t1).100

Aynı orantıyı (kısmi) buhar basınçlarının oranı olarak ta ifade edebiliriz.

rH (%)=(P_wv-t1/P_wv-dp-t1).100

 

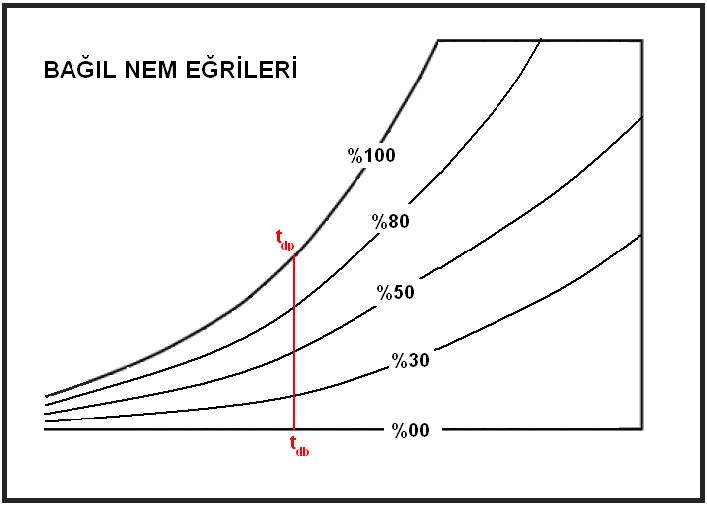
Yukarıdaki psikrometrik diyagramdan da anlaşılacağı gibi “t_db”kuru termometre şartlarındaki bir ortamda olabilecek mutlak nem oranı (miktarı) sıfır ile “t_dp”nin tekabül ettiği nem oranı arasında değişiklik gösterebilmektedir. Belirtilen sıcaklıktaki mutlak nem miktarının yüzde ellisi “rh%50”i,yüzde sekseni “Rh%80”i, yüzde otuzu da “Rh%30”a tekabül etmektedir.

Burada bilinmesi gereken bir olay vardır. Gün batımına yakınlaştıkça bağıl nem oranı artar. Bu işlem havanın duyulur soğuma işlemine tabi olmasından kaynaklanmaktadır. Havadaki mutlak nem değişmediğinden soğumaya bağlı olarak bağıl nem oranı artış gösterir. Bu soğuma devam eder ve çiy noktası sıcaklığının altına düşerse, örneğin arabalarımızın camlarında gördüğümüz su zerreciklerini görürüz. Eğer sıcaklık 0^oC’ın altındaysa çiy yerine kırağı ile karşılaşırız.

3.6. Barometrik Basınç 

Basınç bir birim alana onun üzerindeki kütlenin ağırlığı ile tatbik olunan kuvvete verilen isimdir. Aynı şekilde barometrik basıncı da herhangi bir belirgin konumda birim alana üzerindeki havanın ağırlığı ile tatbik olunan kuvvet olarak tarif edebiliriz. Psikrometrik proseslerde barometrik basınç ile atmosferik basınç eş anlamlı olarak kullanılmaktadır.

Barometrik basınç deniz seviyesinden olan irtifa ile değişmektedir. Atmosferin belirli bir kalınlığı olduğu kabulü ile barometrik basıncın deniz seviyesinden derinlere inildiğinde artacağı, yükseklere çıkıldığında da azalacağı kolaylıkla anlaşılabilir. Barometrik basınç “barometre” olarak adlandırdğımız, genelde cıva içeren bir ölçme aleti ile ölçülür. ASHRAE STP tarifine göre deniz seviyesindeki basınç 29.92 inHg, 760mmHg veya 101.325 kPa (kilopaskal)’dır. Günümüzde cıvalı barometrelere ilaveten körüklü “aneroid” tipi veya spiralli mekanik barometreler ve elektronik dijital barometreler de kullanılmaktadır.

Eğerbelirli bir noktadaki barometrik basınç bilinmiyorsa, basıncı ICAO (Uluslar arası Sivil Havacılık Kurumu)’nun 1925 yılında yayınlamış olduğu formüle göre hesaplamak mümkündür. Konu 2.4.1’de vermiş olduğumuz formülü tekrar veriyoruz.

P_bar= 101.325 (1-2.25577 x 10^-5x Z)^5.2559……….(kPa)

 Buformülde “Z” metre cinsinden irtifayı göstermektedir. İrtifaya bağlı olarak basınç ve sıcaklık değerlerinin değişimi Konu-2.4.1’deki “Standart Atmosferik Doneler” tablosunda -500m ila 10 000m arasındaki irtifalar için gösterilmektedir.

Barometrik basınç kuru havanın basıncıyla su buharının basıncının toplamından oluşmaktadır. Herhangi bir belirgin konumdaki barometrik basıncı  birim alan üzerindeki havanın ağırlığı ile tatbik olunan kuvvet olarak tarif etmiştik. Ancak havanın özgül hacminin artması ki bu genellikle sıcaklık artışına bağlı olarak meydana gelir, kuru hava basıncının azalmasına neden olur. Barometrik basınç sabit olduğuna göre eksilen kısmi basıncı su buharı tamamlayacaktır.

P_bar= P_da + P_wv

Diğer bir yaklaşımla, kuru havanın basıncındaki değişikler barometrik basıncı oluşturan ikinci ögeyi etkilediğini, bu nedenle kuru hava kısmi basıncının azalması su buharı kısmi basıncının artmasına neden oluşturduğunu söyleyebiliriz. Aynı şekilde kısmi kuru hava basıncındaki artışlarda kısmi buhar basıncında eksilmelere neden oluşacağı, bu işlemin de havadaki su buharının yoğuşması suretiyle gerçekleşeceği psikrometrinin temel oluşumlarından biridir.

Psikrometrik prosesler esnasında barometrik basıncın sabit olduğu kabul edilir. Tüm klima hesaplarında bu husus aynen kabul edilmekte, meteorolojik olaylar neticesi barometrik basınçta meydana gelebilecek küçük değişmeler kabili ihmal kabul edilmektedir.

 Barometrik basınç psikrometrik özelliklerin belirlenmesi ve sabitlenmesi için gerekli üç temel ögeden biridir. Diğer ögelerin başında kuru termometre sıcaklığı ile yaş termometre sıcaklığı gelir. Yaş termometre sıcaklığı yerine mutlak nem oranını veya bağıl nemi de kullanabilirsiniz. Barometrik basınç psikrometrik diyagramlarda bir koordinat olarak yer almaz. Ancak her barometrik basınç için ayrı bir psikrometrik diyagramın çizilmesi gerekir. Bu nedenledir ki ASHRAE deniz seviyesi (101.325 kPa) için ayrı, 750 metre (92.834 kPa) için ayrı, 1500 metre (84.556 kPa) için ayrı ve 2250 metre (77.058 kPa) için ayrı psikrometrik diyagramlar tanzim etmiştir. Bu diyagramlar 4. Bölüm’de detaylı olarak incelenecektir.

Barometrik basıncın irtifa nedeniyle azalması da hava içinde bulunabilecek mutlak nem oranını etkilemektedir. Basıncın düşmesi neticesi kısmı buhar basıncı ve buna bağlı olarak mutlak nem oranı artmaktadır. Bu değişikliği aşağıdaki diyagramda görebiliriz.

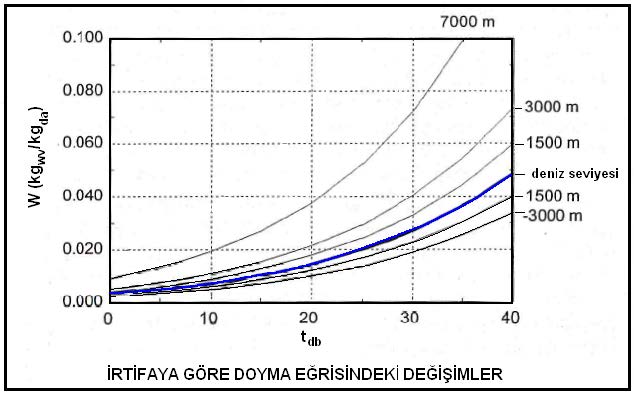
Ref.:Understanding Psychrometrics, Donald P. Gatley, ASHRAE

3.7. Özgül Hacim

Özgül hacim psikrometride kuru havanın birim kitlesinin işgal ettiği hacim olarak tarif edilir. Birimi beher kilogram başına düşen metreküp olup “m³/kg_da” olarak gösterilir sembolü de “v” harfidir. Dalton Kanunu’na göre kuru havanın, su buharının ve nemli havanın işgal ettikleri hacimler birbirine eşittir. Bu nedenle salt “v” ile iktifa edilir ve alt simge kullanılmaz.

Psikrometrik diyagramda özgül hacim eğimli düz çizgiler olarak gösterilir.

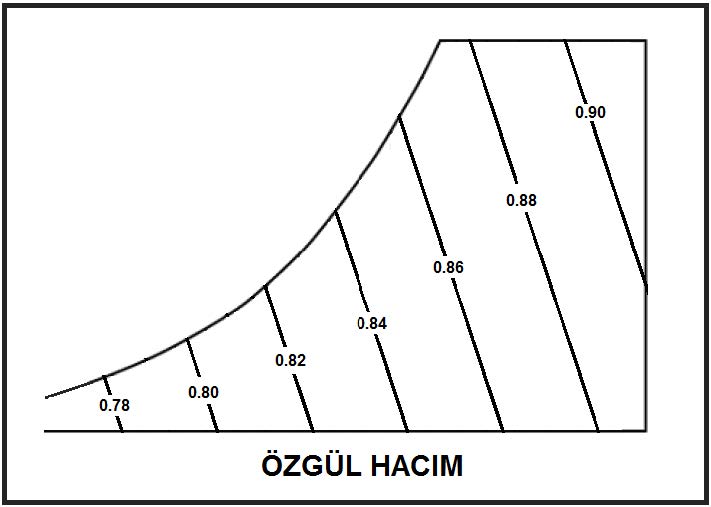
Psikrometrik özgül hacmin tarifi içinde kuru hava ile su buharından başka gazlar dikkate alınmamaktadır. Bu nedenle psikrometrik özgül hacim bilimsel özgül hacim tarifinden az da olsa farklılık içermektedir. Psikrometride özgül hacim nemli havanın hacminin kuru havanın kitlesiyle bölünmesiyle bulunur (m³/kg_da). Ancak diğer bilimsel uygulamalar için özgül hacim tüm elemanları içeren hacmin aynı elemanları içeren birim kütleye bölünmesiyle elde edilir.  İdeal gazları Dalton Kanunu’nun ışığı altında incelediğimizde karışımı meydana getiren kuru havanın ve su buharının aynı hacmi işgal ettiklerini görürüz. Bunu denklem olarak yazdığımızda:

V_da/m_da=V_wv/m_da=V_a/m_da

 Bu denklemde:

V= hacim……………………… m³

             M= kitlesel ağırlık…………kg’dır.

 Bu nedenle aynı denklemi özgül hacim açısından aşağıdaki gibi yazabiliriz:

 v_da=v_wv=v_a

Bu eşitlik eşit kuru termometre şartlarında geçerlidir.

 Özgül hacim ideal gazlarla ilgili denklemlerle de ifade edilebilir:

 P_da. v =R_da. T       

 ve

 P_da= P_bar-P_wv

 Bu iki denklemden hareketle aşağıdaki sonuçlara varırız:

v=(R_da.T)/(P_bar-P_wv)

 v=(287.042)(t_celcius+273.15)/(P_bar-P_wv)

 Daha önce,konu 2.4.4’de aşağıdaki eşitlik bulunmuştu

                          W=0.621945 . p_wv/(p_bar – p_wv)

 Bu eşitliği yukarıdaki denkleme yerleştirdiğimizde aşağıdaki sonuca ulaşırız:

v=(287.042)(t_celcius+273.15).(1 +1.60786W)/P_bar….m³/kg_da

3.8. Mutlak Nem Oranı

 Mutlak nem oranı birim hacimdeki kuru hava içinde bulunan nem miktarıdır. Aynı zamanda kısaca mutlak nem olarak ta ifade edilen bu bulgu şu şekilde ifade edilebilir. Mutlak nem oranı deniz seviyesinden olan yüksekliğin bir fonksiyonudur. Bu husus aşağıdaki hesaplarda da görülmektedir.

W=m_wv/m_da……………………………….(kg_vw/kg_da)

Bu formülde:

                W : Mutlak nem oranı

m_wv: Su buharı kitlesi…………………………..kg_vw

                m_da: Kuru hava kitlesi………………………….kg_da

Psikrometrik diyagramda mutlak nem oranı yatay çizgiler olarak gösterilmektedir.

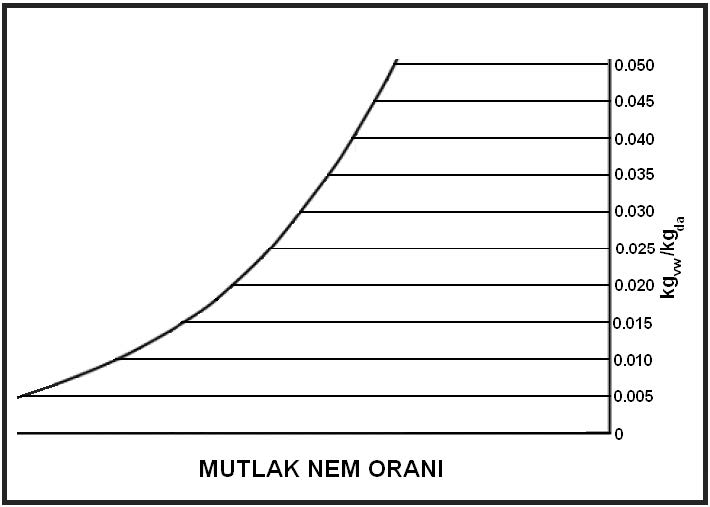
Mutlak nem oranı “W”, su buharı kısmi basıncı “P_wv” ve bağıl nem “rH” arasındaki münasebetleri aşağıdaki gibi belirleyip bu münasebetlerden yola çıkarak mutlak nem oranını hesap yoluyla bulabiliriz. İlk öce ideal gazlarla ilgili genel denklemimizi yazalım, sonra bunlara alt simgeler uygulayarak bu denklemleri su buharı ve kuru hava için tekrarlayalım.

P.V = m.R.T

m= (P.V)/(R.T)

m_da= (P_da.V_da)/(R_da.T_da)

m_wv= (P_wv.V_wv)/(R_wv.T_wv)

R_da= 287.06 J/kg.K)………………   (Bkz. Konu 2.2.4)

R_wv= 461.51 J/kg.K)………………   (Bkz. Konu 2.3.1)

(m_wv/m_da)=W=((P_wv.V_wv)/(R_wv.T_wv))/((P_wv.V_wv)/(R_wv.T_wv))

Bu son denklemde V_wvile V_daDalton kanununa göre eşittirler.Çünkü aynı hacmı paylaşmaktadırlar. Aynı şekilde T_daile T_wvda birbirine eşittir. Bu eşitliklerin birbirini götürmesi halinde formülümüz aşağıdaki şekle döner.

W=((P_wv)/(R_wv.))/((P_wv)/(R_wv))

W=(P_wv.R_da)/(Pda.R_wv)

W=287.06P_wv/461.51P_da

W=0.622 (P_wv/P_da)………………. Bulunur.

P_bar= P_da+ P_{wv……………………….}P_da=P_bar-P_{wv……………}olduğuna göre:

W=0.622 P_wv/(P_bar-P_wv)………………………………bulunur.

Bu son formüle göre mutlak nem oranının, başka bir ifade tarzıyla bir metreküp kuru hava içinde bulunabilecek nem miktarı atmosferik basıncın bir fonksiyonudur. Atmosferik basınç azaldıkça birim kuru hava hacmi içindeki mutlak nem oranı artar. Bu husus Konu 3.9’daki “İrtifaya Göre Doyma Eğrisindeki Değişimler” diyagramında açıkça görülmektedir.

3.9. Buhar Basıncı

Buhar basıncı, atmosferik basıncı meydana getiren kısmi basınçlardan biridir. Bunu daha önceki bahislerde görmüştük. Bu hususu aşağıdaki gibi formülize edebiliriz.

P_bar=P_N2+P_o2+P_Ar+………………………+P_wv

Bu formülde “P_wv” su buharı basıncını, diğerleri ise atmosferi oluşturan sair gazların basıncını ifade etmektedir. Deniz seviyesinde atmosferik basıncın psikrometrik prosesler açısından sabit olduğunun kabul edildiği belirtmiştik. Bu duruma göre deniz seviyesindeki basıncı şöyle de yazabiliriz.

P_bar=P_da+P_wv=101.325 kPa

Bu bağlantıdan iki husus anlaşılmaktadır.

• Kuru havanın basıncındaki artmalar ve eksilmeler buhar basıncını belirler.
• Atmosferik basıncın deniz seviyesinden olan yüksekliğe bağlı olarak değişmesi hem kuru hava kısmi basıncını hem de su buharı kısmi basıncını etkiler.

Kısmi buhar basıncını mutlak nem oranına bağlı olarak şu şekilde hesaplayabiliriz:

W=0.622P_wv/(P_bar-P_wv)…………….(bkz. Bölüm-3, konu 3.8)

P_wv=1.6077W(P_bar-P_wv)

veya

P_wv= W(162.90 – 1.6077P_wv)  …………………….(bulunur)

Deniz seviyesinde doyma noktasındaki buhar basıncı da P_bar’ın yerine 101,325 Pa değerini koymakla bulunur.

Değişik irtifalar için kısmi buhar basıncını değişik bir yöntemle  aşağıdaki gibi hesaplayabiliriz. Bunun için Bölüm-2 , konu 2.4.1’deki basınç hesaplama formülünü “P_wv” formülüne monte etmemiz gerekir.

P_bar=101.325(1 – 2.25577 x 10^-5x Z )^5.2559….dolayısıyla

P_wv=1.6077W(101.325(1 – 2.25577 x 10^-5x Z )^5.2559-P_wv)

Bu formülde “Z” metre cinsinden deniz seviyesinden yüksekliği göstermektedir.

Aynı noktadan hareketle Bölüm-2 konu 2.4.3’deki empirik formülü kullanarak deniz seviyesinde, değişik sıcaklıklardaki doymuş buhar basınçlarını hesapladığımızda aşağıdaki tablodaki değerleri buluruz.

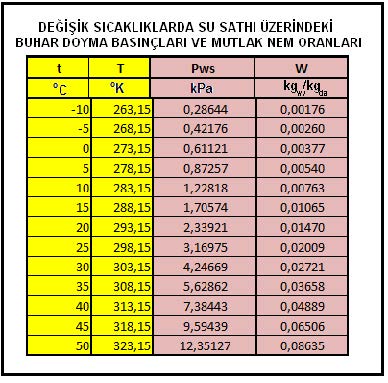
Yukarıdaki tablodan ve formüllerden de görüldüğü gibi buhar basıncı ile mutlak nem oranı birbiri ile birinci dereceden doğru orantılıdır. Bu noktadan hareketle psikrometrik diyagramda buhar basıncı ve mutlak nem çizgilerinin doğrular tarzında, birbirlerinme paralel olduğu, aynı zamanda absise de paralel olduğu anlaşılır. Bu durum aşağıdaki şematik çizimde gösterilmektedir.

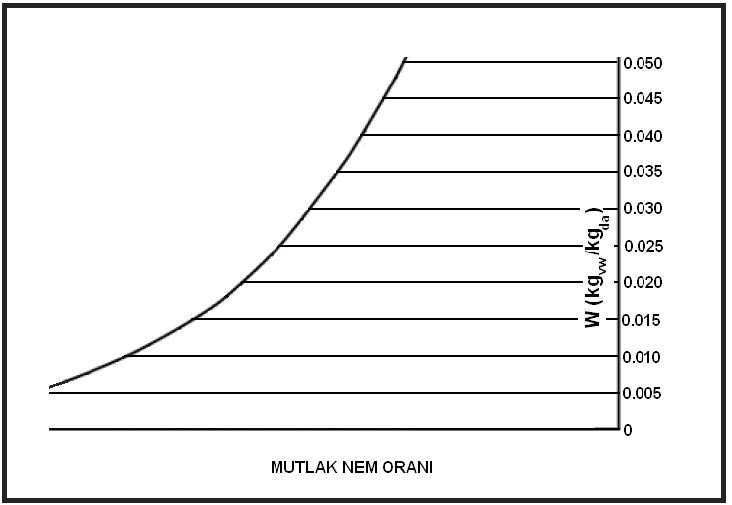
3.10. Özgül Entalpi

Entalpi maddenin yapısında depolanan her türlü enerjinin toplamıdır. Ancak maddelerin kesin entalpilerinin hesaplanması oldukça zordur. Bu yüzden çalışmalarda entalpik değer olarak birim kütledeki maddenin, belirli bir referans noktasından mevcut sıcaklığa yükselebilmesi için gerekli olan enerji ile faz değiştirmesi için gerekli olan enerjinin toplamına denir. Sıcaklık yükselmesi için gerekli entalpi “kJ/kg.” olarak ifade edilir. Keza aynı durum buhar için de gereklidir. Ayrıyeten sabit sıcaklıkta faz birim kitlenin faz değişimi için gerekli ısıya da  prosese bağlı olarak buharlaşma antalpisi veya yoğuşma antalpisi denir.

Birim kütleye sahip maddelerin birim sıcaklık artımı için gerekli ısıyı alabilme kapasitesine “özgül ısı” denir. Önceki yıllarda 1 kilogram suyun sıcaklığının 1^oC artması için gerekli ısı miktarı 1 kCal/^oC.kg kabul edilmiş ve değer arı suyun özgül ısısı olarak kabul edilmişti. Bu kabulden hareket ederek diğer sıvı, katı ve gaz konumundaki maddelerin sabit basınç altındaki özgül ısıları “c_p” belirlenmişti. Günümüzde artık“SI” birimleri kapsamında “kJ/kg.^oC” kullanılmakta ama aynı orantı mantığı devam etmektedir.

Antalpi “h” sembolü ile ifade edilir. Kuru hava için bunu aşağıdaki gibi formülize edebiliriz.

h_da=c_p(Δt)……………………………….kJ/kg

Kuru havanın antalpik ölçümleri için 0^oC noktası referans alınmıştır. Bu sıcaklığıjn altındaki kuru hava antalpileri “-“, üstündekiler ise “+” olarak ifade edilmektedir. Bu açıdan konuya baktığımızda yukarıfaki formül şu şekli alır:

h_da=c_p(t) .……………………………….kJ/kg

Önceki bahislerde, örneğin bu bölümde konu-3.2’de kuru hava ve su buharı için özgül ısı değerleri verilmiştir. Bu değerleri kullanarak kuru havanın entalpisini hesaplamak mümkündür. Ancak psikrometrinin incelediği hava salt kuru hava olmayıp kuru hava ile su buharının karışımından meydana gelmektedir. O zaman havanın antalpisi şu şekilde ifade dilebilir:

h_a= h_da+W.h_wv.……………………………….kJ/kg

Bu formülde:

h_a= Nemli havanın entalpisi……………….kJ/kg

h_da= Kuru havanın entalpisi……………….kJ/kg

h_wv= Su buharının entalpisi…………….….kJ/kg

                       W  = Mutlak nem oranı………………………kg_wv/kg_da

Yaklaşık denklemler olarak, havanın özgül ısısının 1.006 kJ/kg.^oC  kabulü ve “h_wv” değerinin kuru termometre sıcaklığına bağlı  aşağıdaki denklemle hesaplanacağını kabul edersek havanın entalpisini aşağıdaki denklemlerle hesaplayabiliriz (ref. Pyschrometrics, Theory & Practice, ASHRAE, 1996, formül No 1.7.21, 1,7,22 ve 1.7.23=;

h_wv= 2501 + 1.805t   

h_a= 1.006t+W.(2501 + 1.805t)………………………..kJ/kg

Yaş termometre sıcaklığı ile ilgili bölümde suyun hava içinde buharlaşmasının adyabatik bir proses olduğunu, dışarıdan herhangi bir enerji almadığını, buharlaşmak için gerekli olan ısıyı kuru havadan aldığını belirtmiştik. Başka bir tabirle yaş termometreyi belirleyen işlemlerde su buhar karışımının başlangıçta ve nihayette antalpik değerlerinin aynı kaldığını söylemiştik. Bu nedenle özgül entalpi hatlarının belirli bir eğimde düz çizgiler olduğunu ve bu çizgilerin yaş termometre çizgilerine paralel olduğunu söyleyebiliriz.

Bunun tek istisnası havaya püskürtülen suyun aşırı soğutulması veya aşırı ısıtılmasıdır ki bu durumda proses çizgisi artık sabit entalpi hatlarına paralel olmaz. Bu konuyu 5’inci Bölüm “Psikrometrik Esasların Uygulanması”da detaylı bir biçimde inceleyeceğiz.

 

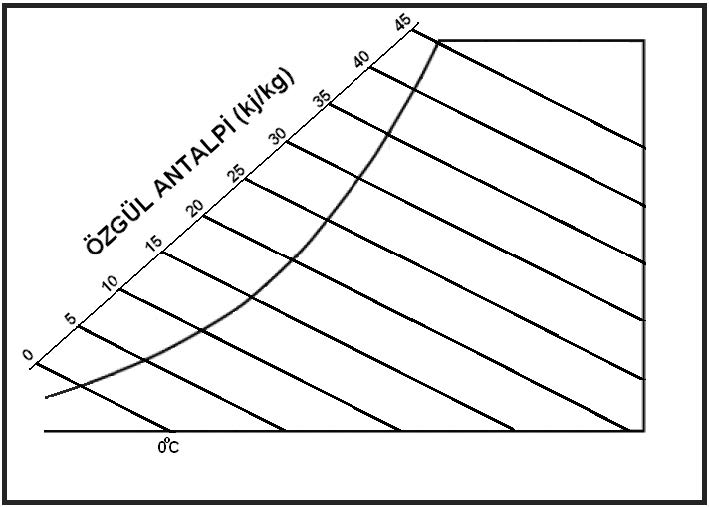
3.11. Özgül Entropi

Termodinamiğin ikinci yasasına aynı zamanda entropi de denir. Düzensizlik entropi ile eş anlamlıdır. Entropi termal işlemlerde yönü belirler. Örneğin suyun yukarıdan aşağı, ısının sıcaktan soğuğa akması gibi. “s” sembolüyle gösterilen özgül entropi sisteme ilave dilen birim enerjinin “dQ” zamana bölünmesinin integraline eşittir . Gibbs teorisine göre gaz karışımının entropisi onu meydana getiren elemanların entropilerinin toplamına eşittir.

s_a=s_da+ W.s_{wv…………………………………………………………………….}.kJ/kg.^oK

Psikrometrik proseslerde ilmi çalışmalara dışında pek karşılaşmayacağınız bu konuya salt bilgi açısından değinmekle yetineceğiz

2. KURU VE NEMLİ HAVANIN TERMODİNAMİK ÖZELLİKLERİ

2.1 Giriş

Atmosfer azot, oksijen, küçük miktarlarda başka gazlar, su buharı ve duman, polenler, ve havayı kirleten atık gazlardan oluşmaktadır.  Bu karışım bazı kitaplarda “atmosferik hava” veya “nemli hava” olarak adlandırılmaktadır. Biz kitabımızda “atmosferik hava” tabirini hiç kullanmayacağız. Çünkü bu tabir Dünya’mızın tamamını saran, troposfer ve stratosferden oluşan hava kütlesine de verilen isimdir. Halbuki psikrometri yalnızca troposferin alt seviyelerindeki hava ile ilgilenmektedir. Bu nedenle yanıltıcı olabileceğini düşündüğümüz “atmosferik hava” tabiri yerine “hava” tabirini kullanacağız. Bu tabiri “nemli hava”, “kuru hava” ve “su buharı” olarak genişletebiliriz. “Nemli hava”  havadan içerdiği iki elemanla ayrılmaktadır. Bunlar “kuru hava” ve “su buharı”ndan oluşmaktadır. Kuru hava ise içindeki su buharından, havayı kirleten duman, polen ve atık gazlardan arındırılmış teorik bir kavramdır.

Psikrometrinin üzerinde çalıştığı eleman havadır ve bu hava daima iki komponentin, su buharı ile kuru havanın karışımından oluşmaktadır. Bu karışım oranı sabit olmayıp , kuru termometre sıcaklığı, deniz seviyesinden yükseklik gibi şartlara bağlı olarak değişiklik göstermektedir.

2.2 Kuru havanın yapısı

Birinci komponent olan kuru hava hacimsel olarak %78 Azot, %21 Oksijen, %1 Argon, küçük ve değişik oranlarda asgari sekiz ayrı gazın oluşumundan oluşmaktadır.

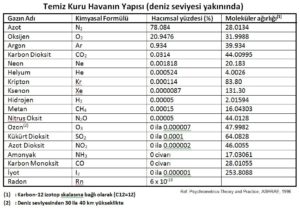
Yukarıdaki tabloda adı geçen gazların tamamı kendi kritik sıcaklıklarının çok üstündedirler. Bu gazların normal atmosferik şartlarda -100^oC ortam sıcaklığının üstünde yoğuşmaları, havayı oluşturan karışımdan ayrılmaları , dolayısıyla havanın oluşumunda bir değişiklik olması söz konusu değildir. Bu nedenle kuru hava tek bir gaz gibi mütalaa edilebilir, psikrometrik proseslere ve psikrometrik tablonun oluşumuna yönelik hesaplara esas alınabilir. Çünü yıllardır yapılan araştırmalar havanın karışımında ve dolayısıyla moleküler kütlesinde çok küçük değişikliklerin olduğu ve bu değişikliklerin psikrometrik değerlerin oluşumunda çok az etki yarattıkları tespit edilmiştir. 1983 yılında Hyland ve Wexler 28.9645 kg/kmol değerini, 2001’de de Nelson ve Sauer 28.95849 kg/kmol’ü havanın molar kütlesi olan olarak hesaplamışlardır. Bizim verdiğimiz “Temiz Kuru Havanın Yapısı” tablosundaki değerler kullanıldığında ise 28.964 kg/kmol bulunmaktadır.

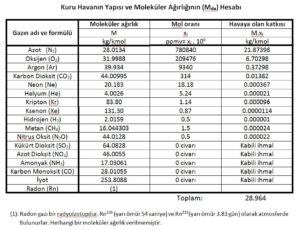
Hesap tarzı aşağıdaki formülde gösterilmiştir.

∑M.x_i= M_N2.x_iN2+ M_O2.x_iO2+ …… + M_I2.x_iI2       ………………. (kg/kmol)

Yukarıdaki tablonun oluşumunu daha iyi anlayabilmek için kullanılan tabirlerin açıklanması gerekmektedir. Bunlardan ilki moleküler ağırlık ve gaz sabitesidir.

2.2.1. Mole (Mol) ve Moleküler Ağırlık:

Mol ve moleküler kütle, bir maddenin (kitlenin yapısına bağlı olarak ve hangisi daha uygunsa) gram-atom veya gram-molekül ağırlığı, 12 gram karbon izotopundaki atom sayısı kadar temel yapıtaşı içeren bir sistemin madde miktarıdır. Temel yapıtaşları atom, molekül, iyon, elektron ve benzeri taneciklerden oluşan gruplar olabilir ve mol kullanılırken belirtilmelidir. Diğer bir anlatımla Bir mol ağırlığındaki bir maddenin kütlesel ağırlığı 6.022×10²³molekül içermektedir. Bu sayı Avogadro Sayısıolarak bilinmektedir. Bir mol da karbon 12 gram ağırlığındaki Karbon 12 örneğinde bulunan atom sayısı olarak ta tarif edilmektedir.

Önceleri 16 olarak kabul edilen oksijen izotopunun ağırlığı esas alınıyordu. Ancak oksijenin değişik izotoplara sahip olması nedeniyle bu sistem terk edildi. 159/60 yıllarında Uluslararası Teorik ve Uygulamalı Fizik Birliği (IUPAP) ile Uluslararası Teorik ve Uygulamalı Kimya Birliği (IUPAC) karbon izotopunun kullanılması konusunda anlaştılar. Her iki kuruluş kütle numarası 12 olan karbon elementi izotopunun (Karbon-12, C¹²) atom ağırlığı, yani atom kütlesi tam olarak 12 olan bu izotopun esas alınması konusunda anlaştılar. Böylece tüm elementler için birleştirilmiş bir bağıl atomik kütlr skalası belirlenmiş oldu.

2.2.2. Mol Oranı:

“x” ile gösterilen mol oranı bir karışımda bulunan bir gazın mol miktarının o karışımda bulunan tüm gazların mol miktarlarının toplamına bölünmesi ile elde edilen sayıdır. Örneğin iki elemanlı bir karışımdaki birinci elemanın mol oranı aşağıdaki gibidir:

x₁=n₁/(n₁+ n₂)

Burada “n₁” ve “n₂” karışımı oluşturan elemanların her birinin mol miktarlarıdır. Bir gaz karışımını oluşturan eleman sayısı kaç olursa olsun mol oranlarının toplamı daima 1’e eşittir.

x₁+x₂+…………….. x_n= 1

2.2.3. Üniversal Gaz Sabiti:

Universal gaz sabiti ideal bir gazın basıncıyla hacminin basıncıyla çarpımının mutlak sıcaklığa bölünmesiyle elde edilen değerdir. Diğer bir deyişle, basınç ile hacmin çarpımının mutlak sıcaklığa olan oranıdır.

P.V= R . T

“R”  ile gösterilen bu sabite bütün gazlar için geçerli olup değeri:               

8.31441 kJ/(kg.mol.^oK)’dir.

2.2.4. Kuru Hava ve Su Buharının Gaz Sabitleri:

Herhangi bir gazın gaz sabiti, üniversal gaz sabitinin o gazın moleküler ağırlığına bölünmesi ile elde edilir.

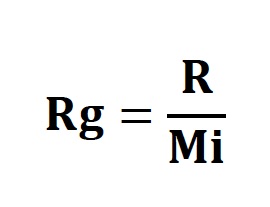 Bu duruma göre azot, oksijen ve kuru havanın gaz sabitleri şu şekilde bulunur:

2.2.5. İdeal Gaz Karışımları :

İdeal gaz karışımları ile ilgili iki temel kanunu hatırlamakta büyük yarar vardır. Bu kanunlar:

• Dalton’un toplanan basınçlar kanunu ve
• Amagat’ın toplanan hacimler kanunu’dur.

Dalton Kanunu’na göre bir gaz karışımının basıncı, karışan gazların karışım sıcaklığında olmaları ve ayrı ayrı toplam hacmi kaplamaları durumunda sahip olacakları basıncın toplamıdır. Amagat Kanunu’na göre de bir gaz karışımının hacmi, karışan gazların karışım sıcaklığı ve basıncında olmaları durumunda yarı ayrı kaplayacakları hacimlerin toplamıdır.

2.3 Su buharı

Psikrometriyi tam olarak anlayabilmek için için H₂O olarak ifade edilen suyun katı, sıvı ve gaz halindeki özelliklerini bütünüyle bilmek gerekir. Birçok madde de olduğu gibi su da üç fazda bulunmaktadır: katı (buz), sıvı (su) ve gaz (buhar veya su buharı). Suyun en büyük özelliği bu her üç fazın da günlük yaşamımızda görülebilmesi ve izlenebilmesidir. Örneğin Yazın bir bardak suya birkaç küp buz koyduğunuzda iki fazı bir arada izlersiniz. Bir müddet sonra bardağın dış sathında su zerrecikleri belirmeye başlar. Bu da yoğuşmakta olan su buharıdır. Bunun nedeni de bardağın dış sathının yoğuşma sıcaklığının altındaki bir sıcaklığa kadar soğumuş olmasıdır. Daha ilerideki bahislerde detaylı olarak ele alacağımız bu konu ile ilgili olarak kısaca şunu söyleyebiliriz: Normal atmosferik şartlarda (STP, Deniz seviyesi, 101.325 Pa basınç) hava içinde bulunabilen maksimum su buharı kuru termometre sıcaklılığna bağlı olarak değişiklikler gösterir. Sıcaklık düştükçe hava içinde bulunabilecek su buharı miktarı azalmaktadır. Bunu da yukarıda bardak örneğinde gördüğümüz gibi satıh yoğuşması ile kendini belli etmektedir. Atmosferik olaylarda ise bu durum kendini yağmur ve kar yağışı olarak belli eder.

Aşağıdaki diyagramda, beher kilogram kuru hava içinde bulunabilecek maksimum su buharı miktarı kilogarm olarak gösterilmektedir.

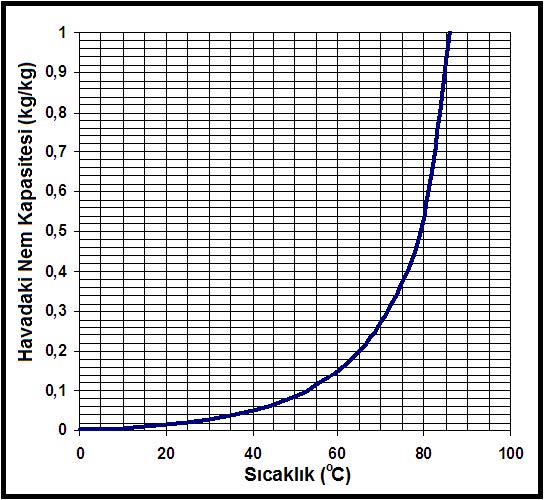
Suyun faz değişiklikleri termodinamik açıdan büyük önem taşır. Katı halden sıvı hale, buzdan suya dönüşmesine “erime” deriz. 0^oC sıcaklıktaki buzun aynı sıcaklıktaki suya dönüşmesi için gerekli ısı ilavesi 333.47 kJ/kg’dır. Bu işlemin tersi de mümkündür buna da donma deriz.

Keza aynı şekilde suyun sıvı halinin gaz haline, suyun buhar haline dönüşmesi için de ısı ilavesi gerekmektedir. Bu miktar da 15^oC muhit sıcaklığında 2465.38 kJ/kg, 100^oC’ta ise 2256.47 kJ/kg’dır. Bir kilogram suyun buharlaşması  için gerekli ısı miktarı 0^oC’ta 2500.93 kJ/kg ile 100^oC’ta 2256.47 kJ/kg arasında değişir.  Su için logP-H diyagramındaki çan eğrisinin içi buharlaşma prosesini göstermektedir. Burada değişik sıcaklıklarda ve basınçlarda suyun buharlaşması için gereken ısı miktarını hesaplamak mümkündür.

Buzun hiç sıvı hale dönüşmeden gaz haline geçmesi de mümkündür. Bu işleme depozisyon tersine de sublimasyon denir. Bu işlem için gerekli olan ısı miktarı da doğal olarak 0^cC’taki erime ısısı ile aynı sıcaklıktaki buharlaşma ısısının toplamına eşittir.

                    H_sub= h_fg1 + h_fg2=333.47 + 2500.93=2834.4 kJ/kg

Burada:

                     h₌ Antalpi (kJ/kg)

                     h_fg1 = Suyun erime antalpisi (kJ/kg)

 h_fg2= Suyun buharlaşma antalpisi (kJ/kg) ‘dır.

Bu değerler aşağıdaki “Doymuş Haldeki Suyun Termodinamik Özellikleri”nde görülmektedir.

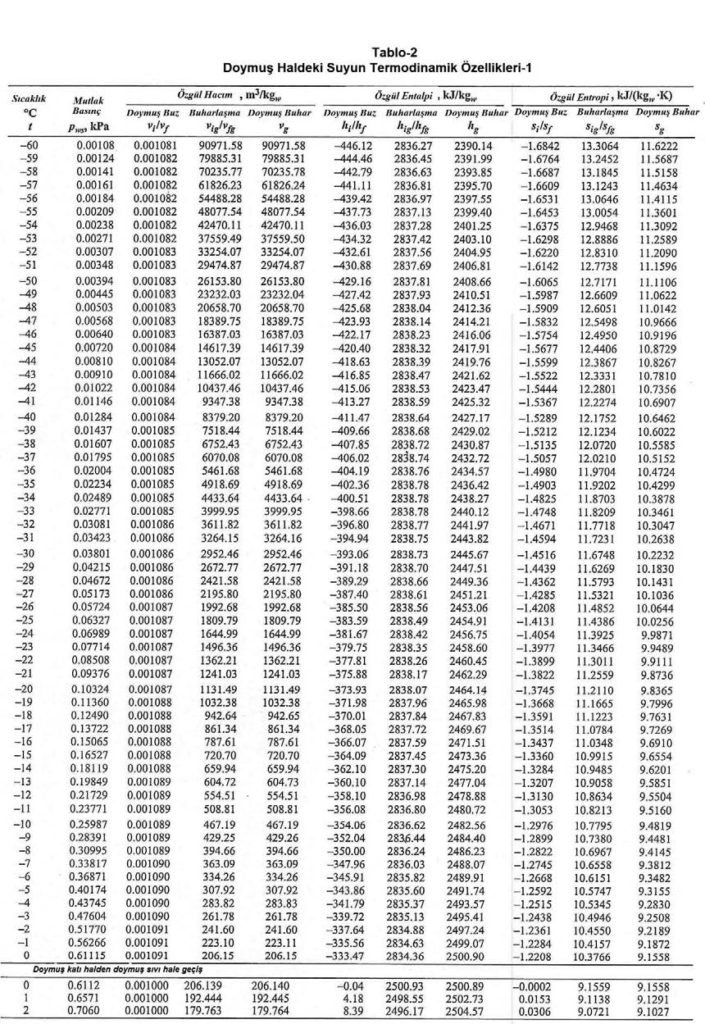
Ref: ASHRAE Fundamentals-2013

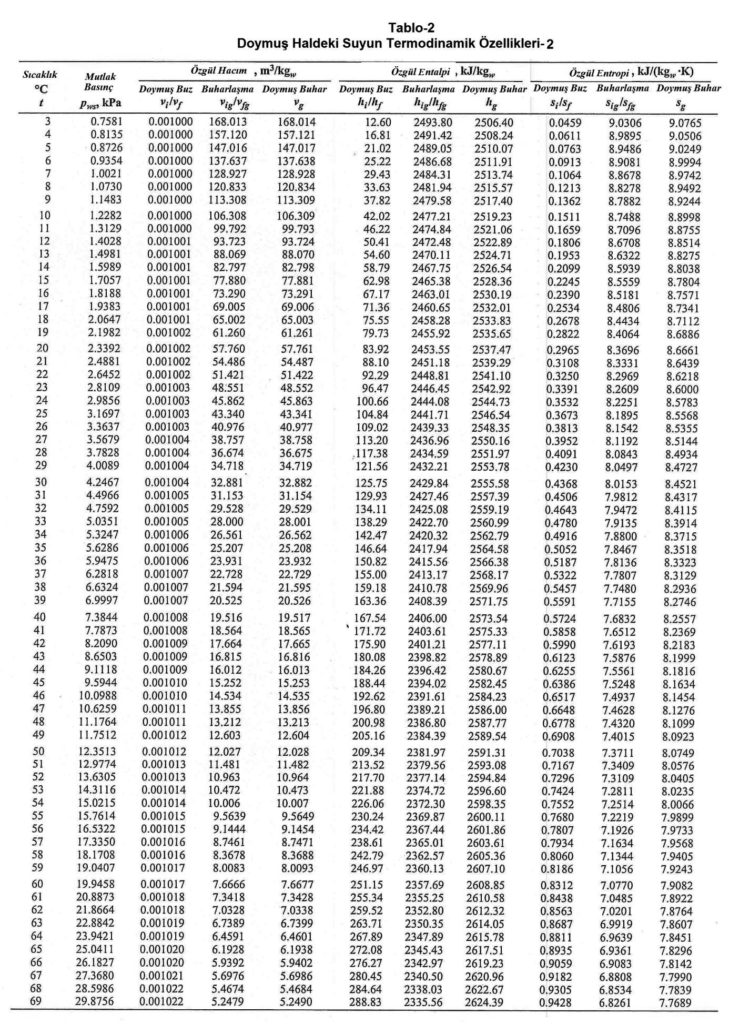
Ref: ASHRAE Fundamentals-2013

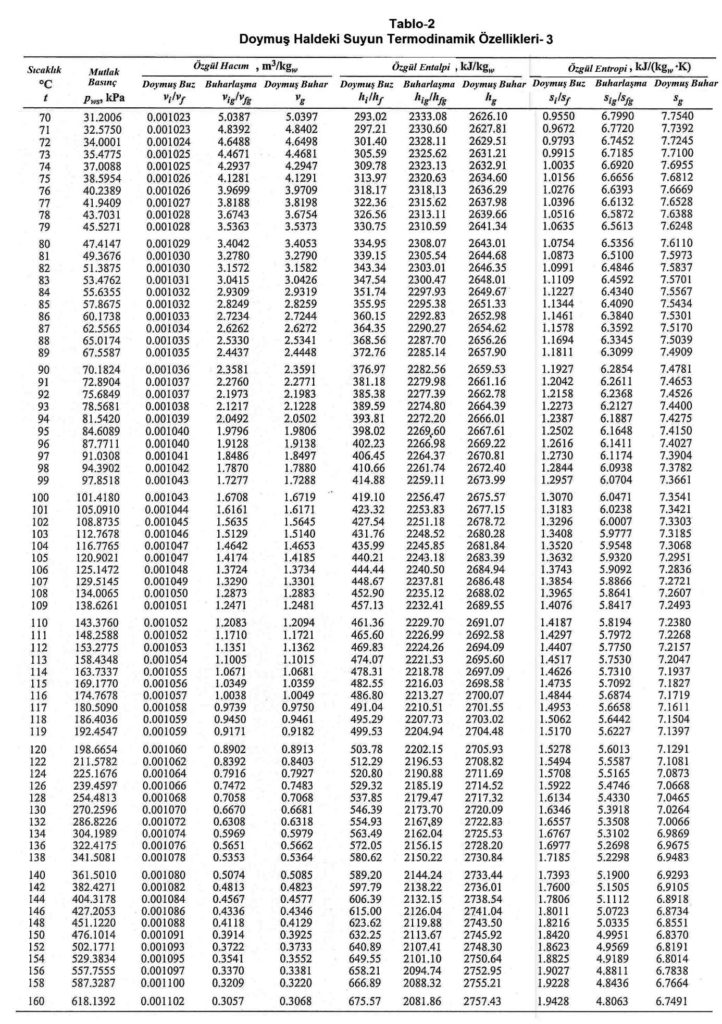
Ref: ASHRAE Fundamentals-2013

2.3.1. Su buharının molerküler ağırlığı ve gaz sabiti

Su buharı iki hidrojen ve bir oksijen atomundan oluşmaktadır. Bu gazların her birinin Karbon-12 skalasına göre moleküler ağırlıkları aşağıdaki gibidir.

M_H2= 2.0159 kg/kmol

M_O2= 31.9988 kg/kmol

M_{H20 (buhar)}= (1 x 2.0159) + ( 0.5 x 31.9988) 

M_{H20 (buhar)}= 18.01534 kg/kMol

2.4. Kuru hava ile su buharının karışımı

Nemli hava, veya bu kitapta kullandığımız tabiriyle hava su buharı ile kuru havanın ikili karışımından oluşur. Kuru havanın homojene yakın karışımına karşılık su buharı ve kuru havanın karışımından oluşan hava homojen değildir. Sıcaklık ve irtifaya göre farklılıklar gösterir.  Örneğin -40^oC’tan daha düşük sıcaklıklarda hava içindeki su buharı oranı sıfıra yakındır. Sıcaklık ve basınca bağlı olarak çok yüksek değerlere ulaşabilir.  Saturasyon veya doyma noktası gaz durumundaki su (buhar)  ile yoğuşarak sıvıya dönüşmüş sıvı (su) arasındaki dengedir.

Teknik tabir olarak yaygınca kullanılan saturasyon kelimesinin kökeni Latince “satar” kelimesidir; “dolu” veya “doyum” manasına gelmektedir. Ancak biz kitabımızda “doyma noktası”tabirini kullanacağız. Su buharı ile kuru hava atmosferde aynı hacmi paylaşmaktadır. İkisinin kısmi basınçlarının toplamı da atmosferik basıncı oluşturmaktadır.  Doyma noktası da belirli bir basınç ve sıcaklıkta birim atmosferik hacim içinde bulunabilecek maksimum su buharı molekülü miktarını ifade etmektedir. Bu  tabir de “gr_{su buharı}/kg_{kuru hava}” veya  “kg_{su buharı}/kg_{kuru hava}” olarak gösterilir.

 

2.4.1. Standart Atmosfer

Atmosferik havanın sıcaklık ve barometrik basıncı irtifa ile ve buna ilaveten mahallin coğrafik ve meteorolojik koşullarına bağlı olarak değişiklik gösterebilir. Standart atmosfer deniz seviyesinde 15^oC ve 101.325 kPa barometrik basınç olarak ifade edilmektedir. Sıcaklığın troposferde irtifaya bağlı olarak lineer bir değişiklik göstereceği, azalacağı, stratosferde ise sabit olacağı belirlenmiştir.

Aşağıdaki tabloda deniz seviyesinden olan irtifaya bağlı olarak sıcaklık ve basınç değişiklikleri gösterilmektedir.

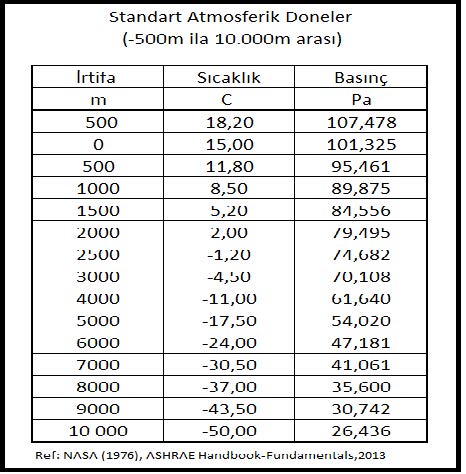
“Standart Atmosferik Doneler” tablosundaki basınç değerleri aşağıdaki şekilde hesaplanabilir:

p= 101.325 (1-2.25577 x 10^-5x Z)^5.2559……….(kPa)

Sıcaklık değerlerinin hesaplanmasında ise şu formül kullanılabilir:

t= 15 – 0.0065 x Z………………………………………(^oC)

Bu formüller 2013-ASHRAE Handbook Fundamentals’da yer almakta olup hatasız bir şekilde -5000 metre ila 11000 metre irtifa arasında kullanılabileceği belirtilmektedir.”Z” deniz seviyesinden olan yüksekliği belirtmektedir.

 

2.4.2. Havanın Termodinamik Özellikleri:

Aşağıdaki tablolarda havanın termodinamik özellikleri verilmektedir. Hermann, Kretzchmar ve Gatley  tarafından 2009 yılında yayınlanan araştırmadaki formüller esas alınarak hesaplanan havanın termodinamik özellikleri aşağıdaki tablolarda verilmektedir. Bu tabloda kullanılan birimler aşağıdadır

t= “Celcius” skalasına göre sıcaklık. “T”olarak gösterilen “Kelvin”

      skalası ile bağlantısı aşağıdaki gibidir:

    T =t + 273.15……………………… (^oK)

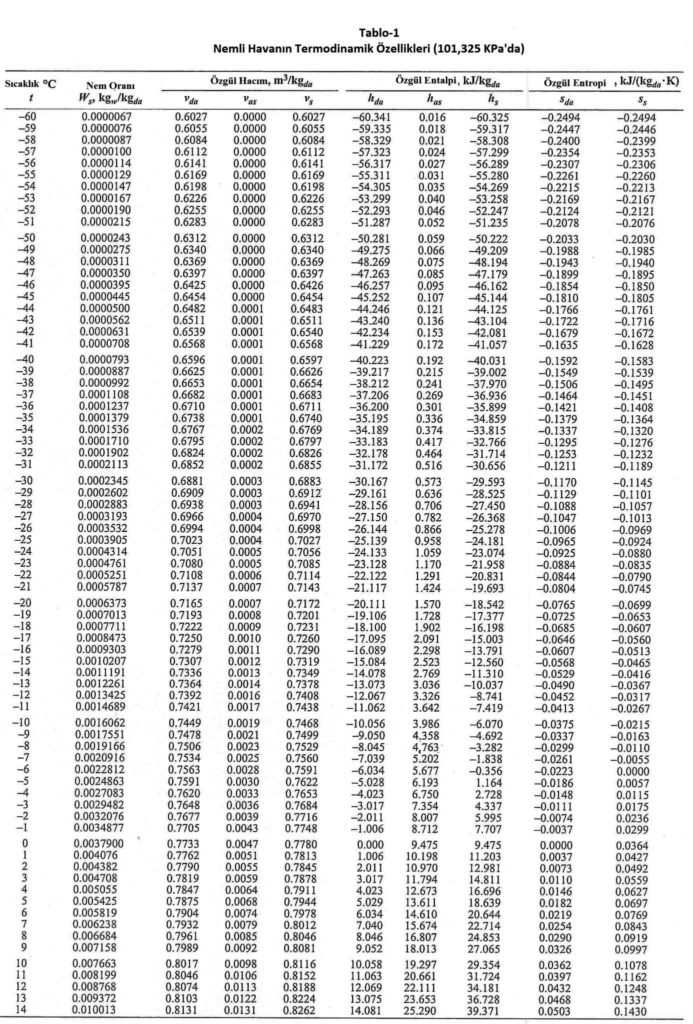
Ref: ASHRAE Fundamentals-2013

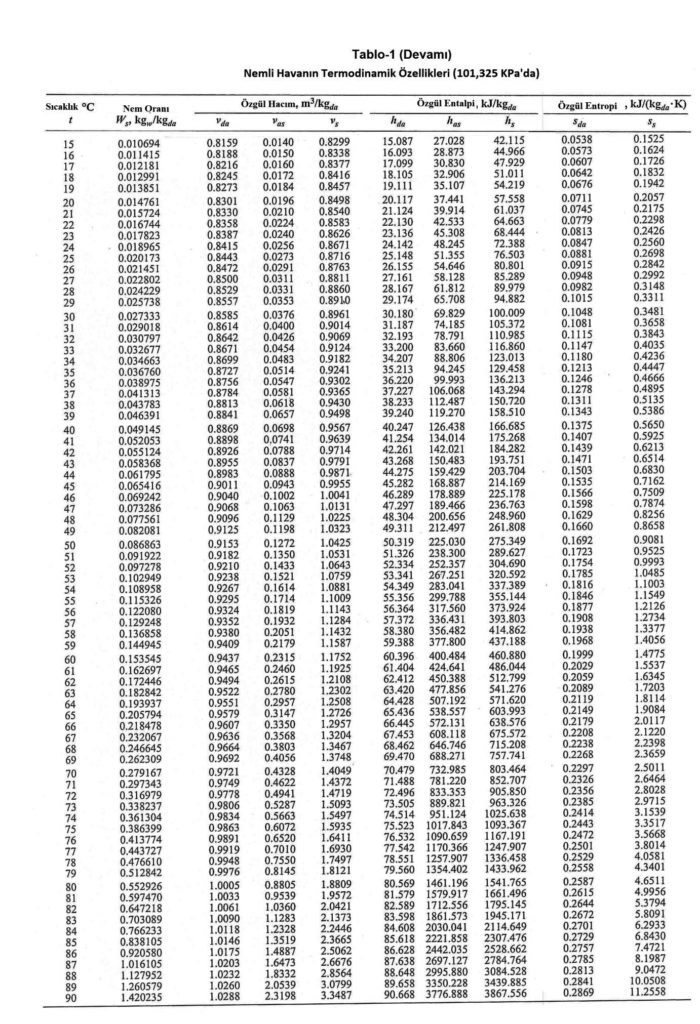
Ref: ASHRAE Fundamentals-2013

Tabloda kullanılan sembollerin açıklamaları da aşağıdadır:

W_s= Doyma noktasındaki su buharı miktarının kuru havaya oranı.

       “kg_w/kg_da” olarak ifade edilir.

v_da= Kuru havanın özgül hacmı  “m³/kg_da” olarak ifade edilir.

v_s   = Doyma noktasındaki havanın özgül hacmı “m³/kg_da” olarak ifade

         edilir.

v_as = Doyma noktasındaki kuru havanın özgül hacmı ile kuru havanın

        özgül hacımları arasındaki fark, “m³/kg_da” olarak ifade edilir.

h_da = Kuru havanın özgül antalpisi. “kJ/kg_da” olarak ifade edilir.

h_s  = Doyma noktasındaki kuru havanın özgül antalpisi. “kJ/kg_da” olarak

        ifade edilir.

h_as = Doyma noktasındaki kuru havanın özgül antalpisi ile kuru havanın

        antalpisi arasındaki fark, “kJ/kg_da” olarak ifade edilir.

s_da = Kuru havanın özgül antropisi, “kJ/(kg_da. K)” olarak ifade edilir.

s_s   = Doyma noktasındaki kuru hava ile kuru havanın özgül antropisi

        arasındaki fark, “kJ/(kg_da. K)” olarak ifade edilir.

2.4.3. Doyma Eğrisi ve Hesaplanması

Psikrometrik proses ve hesaplarda doyma eğrisi çok önemli bir yer işgal eder. Bu eğri aynı zamanda su buharı basıncını ve su buharı doyma sıcaklığını da belirler. Birçok eserde bu şartların belirlenmesi için ASHRAE Handbook-Fundamentals’a refere olunur ve oradaki tabloların kullanılması önerilir. Bu tablolar kitabımızda da verilmektedir. Ancak bu değerlerin hesap yoluyla da bulunabileceğinin bilinmesinde fayda vardır. Çünkü mühendislik bir şeyi olduğu gibi kabul etmek değil, bunun nedenlerini bilmek, empirik te olsa formüller ile bu değerlere ulaşabilmektir. Kullandığımız tabloların çoğu da bu yollarla hesaplanarak bulunmuştur. Buna örnek olarak kanal hesap abaklarını, ısıtma ve soğutma hidronik hesaplarında kullanılan boru hesap abaklarını gösterebiliriz.

Günümüzde en doğru yaklaşımları veren formül IAPWS (International Association for the Properties of Water and Steam) -IF97’de belirtilen formüllerdir.  Sıvı haldeki su sathı üzerindeki doyma basıncının sıcaklığa bağlı olarak hesaplanması aşağıdaki formülle belirlenmiştir.

p_ws=1000 x (2 x C/(-B+(B²-4 x A x C)^0.5))⁴………..(kPa)

Bu formülde :

A= Q²+ (N₁x Q) + N₂

B= (N₃x Q²) + (N₄x Q) + N₅

C= (N₆x Q²) + (N₇x Q) + N₈

“Q” değeri ise aşağıdaki formülle hesaplanır:

Q= T + N₉/(T-N₁₀)

T= t_C+273.15 

“t_C” Celcius skalasına göre doyma sıcaklığıdır.      (^oC)

N₁=  1167.05214527670            N₂= -724213.167032060

N₃= -17.0738469400920            N₄= 12020.8247024700

N₅= -3232555.03223330            N₆= 14.9151086135300

N₇= -4823.26573615910           N₈= 405113.405420570

N₉= -0.238555575678490         N₁₀= 650.175348447980

Bu hesap tarzı (0^oC ≤  t_c ≤ 373^oC için geçerlidir. Aynı şekilde “ters denklem” tabir edeceğimiz işlemle de doyma basıncından hareketle doyma sıcaklığını hesaplayabiliriz.

t_Cdp= (0.5 x (N₁₀+ D –((N₁₀+ D)²-4(N₉+N₁₀x D))^0.5))-273.15

Bu formülde :

D= 2G/(-F-(F²-4E x G)^0.5)

E= β²+ N₃x β + N₆

F= (N₁x β²) + (N₄x β) + N₇

G= (N₂x β²) + (N₅x β) + N₈

“β” değeri ise aşağıdaki formülle hesaplanır:

β= ( p_ws/1000)^0.25………………….. (p_ws= kPa)       

2.4.4. Mutlak Nem Miktarının (Nem Oranının) belirlenmesi

Havadaki mutlak nem miktarı (nem oranı) “W” bir kilogram kuru hava içinde bulunan nem miktarının orantı olarak belirtilmesidir. Bu orantı (kg_wv/kg_da) olarak ifade edilir.

Bağıl nem ise belirli bir kuru termometre sıcaklığındaki mutlak nem miktarının aynı sıcaklıkta doyma noktasındaki mutlak nem miktarına oranıdır. Bu tabir “%” olarak ifade edilir.

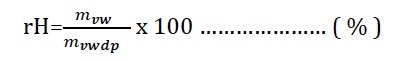
Mutlak nem miktarının hesaplanmasını da aşağıdaki tar-zda ve Dalton Kanunu’ndan yararlanarak yapabiliriz.

p.V = m . R . T

Bu formülü “m” değerini hesaplamak üzere tekrar düzenlersek:

m = (p . V)/( R . T ) 

 bulunur. Aynı formülü su buharı ve kuru hava için düzenlediğimizde aşağıdaki denklemlere ulaşırız.

m_vw= (p_vws. V_vws)/( R_wv. T )  …….. su buharı için

m_da= (p_da. V_da)/( R_da. T )  ………kuru hava için

 m_vw/m_da=((p_wvs. V_wvs)/( R_wv. T ))/( (p_da. V_da)/( R_da. T )) 

 Dalton Kanunu’na göre su buharı ile kuru hava aynı hacmı paylaşmaktadır. Bu nedenle:

V_vws= V_da

 Keza aynı şekilde her iki gazın ortam sıcaklığı da birbirlerine eşittir. Bu nedenle eşit değerler birbirini götüreceği için denklem aşağıdaki şekle dönüşür.

m_vws/m_da=(p_vws/ R_wv )/(p_da/ R_da) 

 R_wv= 461.52 kJ/kg

R_da= 287.06 kJ/kg

 Bu değerleri yerine koyduğumuzda

m_vw/m_da=0.621945 . p_vw/p_da       bulunur.

p_da= P – P_{vws                                      olduğundan aşağıdaki sonuç formül karşımıza çıkar.}

m_vw/m_da=0.621945 . p_wvs/(p– p_wvs)

 2.4.3 No’lu bahiste doyma nokta sıcaklığındaki buhar basıncını ve o noktadan hareketle doyma noktası sıcaklığının hesaplanacağını incelemiştik. Şimdi de o sıcaklığa tekabül eden mutlak nem miktarını buhar basıncına bağlı olarak nasıl hesaplanacağını görmüş olduk.

 2.4.5. Havanın Özgül yoğunluk ve özgül hacminin belirlenmesi

 P.v_{da_0C}= m . R . T

 Bu denklemde :

P          = Atmosferik basınç, 101325 Pa

v_{da_0C}  = Özgül hacım. 0^oC kuru hava için (m³/kg_da)

m         =Havanın moleküler ağırlığı. 28.964 kg/kmol

R          = Üniversal gaz sabiti . 8314.41 J/(kmol.K)

T          = havanın sıcaklığı ( ^oK)

Değerleri denklemde yerlerine koyup, “v_{da_0C}”için çözdüğümüzde:

v_{da_0C}=((8314.41)x(273.15 + 0))/(28.964×101325)

 v_{da_0C}= 0.773851 …………………………….  (m³/kg_da-0C)

 Havanın özgül yoğunluğu: δ_{da_0C}= 1/ v_{da_0C} olduğuna göre:

δ_{da_0C}= 1/ 0.773851=1.2922 … (kg_da-0C/m³) bulunur.

Bu formülü genelleştirdiğimiz zaman, derğişik sıcaklıklardaki kuru havanın özgül hacmini aşağıdaki formülle hesaplayabiliriz.

v_da= 0.0028333 (273.15 + t_da)

 Kuru havanın hesapla bulunan özgül ağırlığına aynı sıcaklıktaki doyma noktasındaki havanın içinde bulunan su buharının ağırlığının ilavesi ile doyma noktasındaki havanın özgül hacmi ve özgül ağırlığı bulunur.

δ_a= δ_da+ W_wv

1. PSİKROMETRİ NEDİR

1.1 Psikrometrinin tanımı ve tarihçesi

Psikrometri Yunanca iki kelimenin, soğuk ve soğutma anlamına gelen “psuchron” ile ölçme anlamına gelen “meter” birleşmesinden oluşmaktadır. Bu kelimeyi ilk kullanan Alman bilim adamı Ernest Ferdinand August’tur. Kendi geliştirdiği ıslak termometreye “Psychrometer”, psikrometre adını vermiştir. Günümüzde psikrometreler kuru termometre ve yaş termometreleri ayrı ayrı ölçmeye yarayan iki termometreden meydanan gelmekte ve bu enstrumanlar higrometre olarak sınıflandırılmaktadır.

Psikrometri sözlüklerde fizik kanunlarına göre kuru hava ve su buharı karışımlarını inceleyen bir bilim olarak tarif edilmektedir. ASHRAE ise psikrometriyi “atmosferik durumların, özellikle hava içindeki nemin ölçümü ve belirlenmesi ile uğraşan, fizik ana bilim dalının bir branşı” olarak kabul etmektedir.  Günümüzde makine mühendisliğinin temel konularından biri olan termodinamiğin içinde de kapsamlı bir şekilde yer almaktadır. Burada önem kazanan bir tarif te “nemli hava”dır. Nemli havayı iki değişik gazın, kuru hava ile su buharının karışımı olarak belirtebiliriz. Kritik sıcaklığın altındaki sıcaklıklarda bir maddenin gaz fazı “buhar” olarak adlandırılır. Bu terim bir maddenin doyma noktasına yakın yerlerdeki gaz halini belirtir. Dolayısıyla bu maddenin hal değişimi esnasında yoğuşabileceği kabul edilir.

Bazı çevreler bu tanımı daha da genişletmekte, psikrometriyi bir maddenin gaz hali ile diğer bir maddenin yoğuşabilir gaz halinin karışımı olarak tanımlamaktadır. Bizim konumuza esas olan ilk tarif ile ASHRAE’in kabulüdür ve bu kitabımızda kuru hava ile su buharının değişik şartlardaki karışımları olarak incelenecektir.

1.2 Psikrometrinin kapsamı

Psikrometri yalnız iklimlendirme dünyasına ait bir çalışma ve inceleme alanından ibaret değildir. Ziraatte, örneğin seralarda ürün yetiştirilmesi için gerekli ortamın tespit ve temininde, tahılların saklanmasında ve kurutulmasında, gıda mühendisliğinde, ilaç sanayiinde, tekstil sanayiinde nem kontrolunda, meteorolojide ve mimaride örneğin iç satıhlarda kondansasyonun belirlenmesi ve önlenmesinde de büyük ölçüde kullanım alanı bulmaktadır.

1.3 Psikrometrik diyagramın gelişimi

Günümüzde yaygın olarak kullanılmakta olan psikrometrik diyagram ilk olarak 1904 yılında Willis H. Carrier isimli Amerikalı bir mühendis tarafından geliştirilmiştir. Ancak prikrometri ile ilgili çalışmalar çak daha öncelere gitmektedir. Antik Yunan Medeniyeti’nde Anaksimenes, Aristo, Hero gibi filozof ve bilim adamlarının çalıştıkları bilinmektedir. “Aer” kelimesinin kökeni de Antik Yunanca olup hava ve su buharı manâsına gelmektedir ve uluslararası literatüre Anaksimenes tarafından kazandırılmıştır.

Aristo’nun ölümünü takiben, onbeşinci yüzyılın başlarına kadar süren Avrupa’nın “Karanlık Yıllar” olarak ta adlandırılan Orta Çağ döneminde hemen hemen hiçbir şeyin yapılmadığını, ancak Rönesans ile çalışmaların Yeni Çağ’da tekrar başladığını görürüz. Leonardo da Vinci (1452-1519) ilk higrometrenin teknik resimlerini tamamlamış ve bu çalışmasına “higroskop” adını vermiştir. İtalyan bilim adamı, matematikçi ve astronom Galileo Galilei (1564-1642) 1593’de başarısız bir termoskop tasarımı girişinde bulunmuştur. Ancak bu başarısızlığa rağmen, takibeden yıllarda gaz hacminin değişmesinin sıcaklık değişimi ile ilgisi hakkındaki prensipleri belirlemiştir. Basınç ölçümünün öncesi ise hiç süphesiz Evangelista Toriçelli’dir (1608-1647). 1643 yılında civalı barometreyi keşfetmiştir. Bu arada konuya büyük katkıları bulunan Blaise Pascal, Robert Boyle, fahrenhayt termometre skalasını geliştiren Gabriel Daniel Fahrenheit (1686-1736), Bernoulli, suyun donma ısısı 0⁰C, kaynama noktasını da 100⁰C olarak belirleyen ve arayı 100 eşit dilime bölerek celsiyus skalasını kazandıran Anders Celsius’u da (1701-1744) belirtmemiz gerekir. Bu termometrelerde skalanın belirlenmesi esnasında içine daldırılmış termometre bulunan suyun ısıtılma suretiyle buharlaştırılması, aynı suyun buharlaştırılması esas alınmıştır. G.D. Fahrenheit taksimatı önceden belirlenmiş bir cetvelde suyun +32^o’de ergidiğini, +212^o’de de buharlaştığını tespit etmiştir. A. Celcius ise bu skalayı 100 eşit parçaya bölmüş, suyun donma noktasına 0^o, kaynama noktasına da 100^odemiştir. Her iki deney de deniz seviyesinde, normal atmosferik şartlarda gerçekleştirilmiştir.

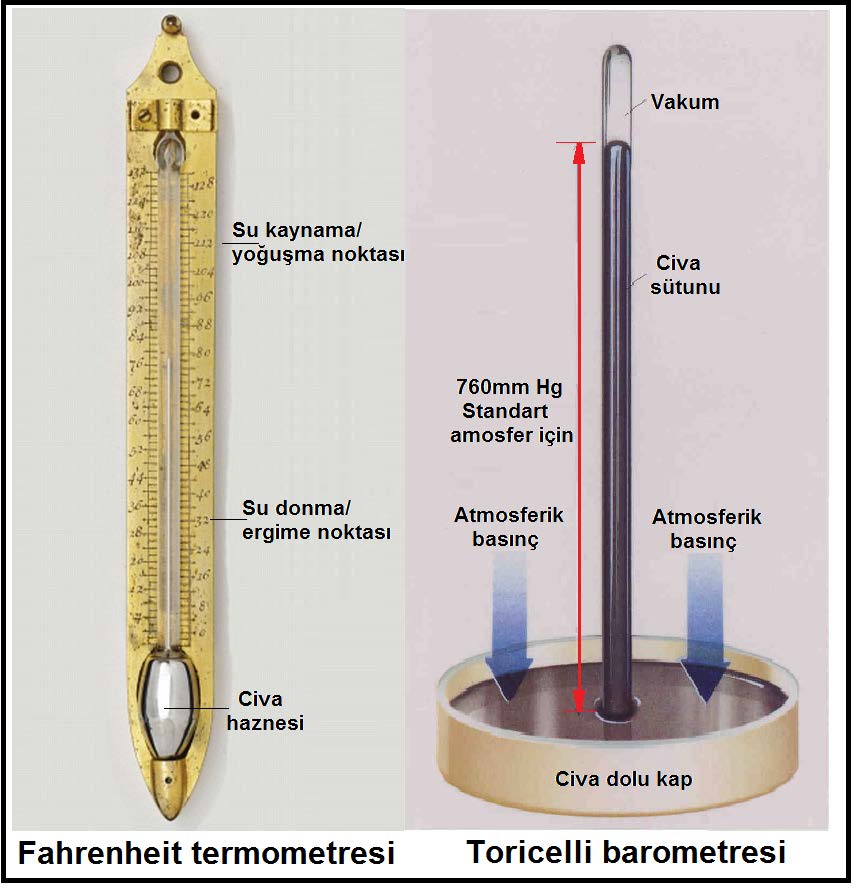
Bu çalışmaların her ikisinde de buz kütlesinin erimek için belirli bir enerjiye ihtiyacı olduğu, buz erirken sıcaklığın değişmediği tespit edilmiştir. Bu işlem için gereken birim ısıya bilahare donma (erime) antalpisi denilecektir. Benzeri durum buharlaşmada da gözlenmiştir. Suyun tamamı buharlaşana kadar sıcaklık değişmemekte ancak ısı ilavesi devam etmektedir. Bu birim ısıya da buharlaşma (yoğuşma) antalpisi denilecektir.

18’inci yüzyılın başlarından itibaren kuru hava ile su buharının ilişkilerini birlikte incelendiğini görürüz. İlk olarak John Dalton (1766-1844) isimli İngiliz bilim adamı havanın genleşmesi ve atmosferik yoğuşmayı, atmosferdeki su buharınının gösterdiği değişimlere dayandırırarak izah etmiş ve modern meteorolojinin temellerini atmıştır. 1801’de geliştirdiği toplanan basınçlar kanunu modern psikrometrinin temelini oluşturan dört ana ögeden biridir (bu konu ilerideki bahislerde kapsamlı olarak ele alınacaktır). Emile Hilaire Amagat (1841-1915) isimli Fransız fizikçi de  toplanan hacimler kanunu’nu bulmuştur. Bu kanun da modern psikrometrinin ikinci temel ögesini oluşturmaktadır.

James Ivory (1765-1842) James Hutton’ın yapmış olduğu yaş termometre deneylerini analiz ederek yaş termometre hakkındaki ilk teoriyi “The Hygrometer by Evaporation” isimli eserinde yayınlamıştır. Teorisini termometrenin ıslatılmış haznesi üzerinde sakin bir hava hareketi olduğunu, su ile hazne arasında ihmal edilebilecek derecede küçük bir ısı iletimi (kondüksiyonu) meydana geldiğini hipotezine dayandırmıştır. Bu işlem esnasında ıslatılmış hazne üzerinden geçen havanın doyma noktasına erişeceği, bu durumda da buharlaşma suretiyle havaya eklenen su buharının buharlaşma gizli ısısının (h_FG-WV-@WB) havadan temin edildiği ve bu surette havanın ısısının düştüğünü, düşen ısı miktarının tekabül ettiği “ΔT” sıcaklık farkının havanın kuru termometre sıcaklığından düşülmesi ile yaş termometre sıcaklığının elde edileceğini ispatlamıştır. Buna ilaveten buhar basıncı ile ilgili olarak aşağıdaki empirik formülü geliştirmiştir.

e = e’ – b ( t – t’)/1200

Bu formülde:

e      = su buharının hakiki basıncı ( inç civa sütunu )

                              e’       = yaş termometre sıcaklığındaki doyma noktasında su

buharının basıncı (inç civa sütunu )

                              t         = Ölçülen kuru termometre sıcaklığı (^oC )

                              t’        = Ölçülen yaş termometre sıcaklığı  (^oC)

                              b        = Barometrik basınç (inç civa sütunu)

Bu formül geçen zaman içinde yapılan küçük değişikliklerle geçerliliğini korumaktadır. “b” faktörü “a.P”ile değiştirilmiş olup “P” barometrik basınç, “a”ise düzeltme faktörüdür.  USWB “United States Weather Bureau” da bu formülde küçük bir düzeltme yapmıştır. Bu düzeltme suyun buharlaşma gizli ısısının kuru termometredeki değişiklikler paralelinde yaptığı değişmeleri kapsamaktadır. Bu formül aşağıdaki gibidir.

(C_p-DA+  C_p-WVS) x (t_DB– t_WB-SAT) = (h_FG-WV-@WB) x ( w_WB– w_ACT)

                            Bu förmülde:

C_p-DA             = Özgül ısı; kuru hava (1.006 kJ/kg.^oC)

C_p-WVS           = Özgül ısı; doyma noktasındaki su buharı (4.186 kJ/kg.^oC)

                           t_DB                   = Kuru termometre sıcaklığı (^oC)

                           t_WB-SAT        = Yaş termometre sıcaklığı, doyma noktasında (^oC)

h_FG-WV-@WB =Suyun buharlaşma spesifik antalpisi, yaş termometre

                                                       sıcaklığında (kJ/kg)

                           w_WB                 = Mutlak nem , doyma noktasında (kg_WV/kg_DA)

                           w_ACT                = Mutlak nem, ölçülen (kg_WV/kg_DA)

Bu arada adyabatik proseslerde ideal gazların basınç, sıcaklık değişmelerindeki durumlarını formülize eden Simeon Denis Poisson’u da (1781-1840) unutmamak gerekir. Bu formüller günümüzde termodinamikte, psikrometrik proseslerde özellikle vantilatöre bağlı ısı yükselmelerinin hesabında kullanılmaktadır.

             T . v^(n-1)= Sabit   ,    T . p^(n-1)/n= Sabit   ,       p . vⁿ= Sabit

1809-1903 yılları arasında yaşamış olan astronom ve meteorolojist James Glaisher 1847 yılında su buharı basıncı, atmosferik basınç, yaş termometre ve kuru termometre sıcaklıklarını içeren ilk güvenilir tabloları yayınlamıştır. Amerikalı bilim adamı William Ferrel de (1817-1891) atmosferik basınç, savurmalı psikrometre ile ölçülen yaş ve kuru termometre sıcaklıklarını esas alarak su buharı basıncını hesaplayacak empirik bir formül geliştirmiştir.

Savurmalı psikrometre iki termometreden oluşmaktadır. Bu termometrelerden birinin ucuna ıslatılmış bir kılıf geçirilmekte diğer termometrenin ucu ise açık bırakılmaktadır. Döndürme koluna bir manivela ile bağlı aparat havada hızlı bir şekilde, ıslatılmış kılıf kuruyuncaya kadar döndürülmekte, tam kurumadan her iki termometredeki değerler okunmaktadır. Ucu ıslatılmış termometreden yaş termometre sıcaklığı, ucu açık olan termometreden de kuru termometre sıcaklığı okunmaktadır. Her iki değerle daha önceden hazırlanmış tabloya girerek  bağıl nem belirlenmektedir.  Aşağıda deniz seviyesi için hazırlanış savurmalı psikrometre tablosu görülmektedir. Bu tablo deniz seviyesi için hazırlanmış olup değişik yükseklikler için de mevcuttur. Günümüzde bir referans ölçüm cihazı olarak kullanılmaktadır.

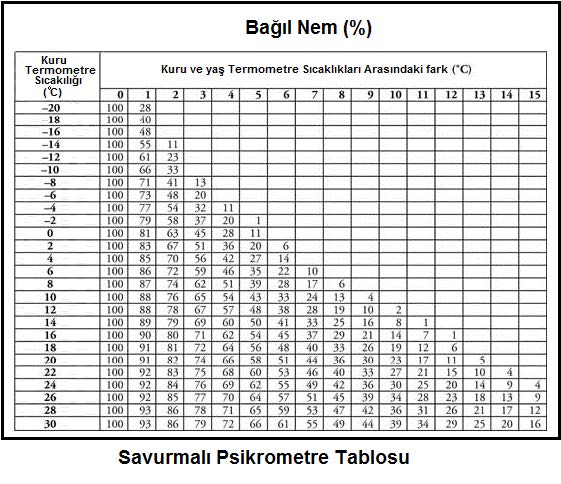
Günümüzde hala kullanılmakta olan diğer bir psikrometrik ölçüm cihazı da aspirasyonlu psikrometredir.

1902 yılında Cornell Üniversitesi’nden mezun olan Willis Haviland Carrier Buffalo Force Co. Şirketinde çalıştığı günlerde, daha bir yıllık mühendisken ilmi esaslara dayanan, rutubet kontroluna yönelik bir klima sisteminin yapımını tamamlamıştı. Böyle bir işin gerçekleştirilmesi için mahallin ısı ve nem kazançlarının (duyulur ve gizli ısı yüklerinin ) hesaplanmasına, nemli havanın psikrometrik  değerlerine ihtiyaç vardı. W.H. Carrier’ın bu donelerin temininde C.F. Marvin’in 1900’da yayınlanan “Psychrometric Tables” isimli eserinden yararlandığı tahmin edilmektedir. 1904 yılında da, mezuniyetinden iki yıl sonra,bugün kullanılmakta olan psikrometrik diyagramlara çok benzer olan “Hygrometric Chart” (Higrometrik Tablo) isimli çalışmasını tamamlamıştı. 1906 yılında yayınlanan Buffalo Force Co. kataloğunda bu tablo yer almıştı. 1911 yılında da ASME’ye “American Society of Mechanical Engineers” (Amerikan Makine Mühendisleri Derneği)sunduğu  “Rasyonel Psikrometik Formüller” isimli çalışmasında Ferrel’in çalışmalarını esas alan termodinamik formüller sunmuştu. Bu formüller sayesinde havanın adyabatik doyması esnasında duyulur ısının gizli ısıya dönüştürülmesini doğru bir şekilde hesaplamak mümkün olmaktaydı.

Pekiyi, Carrier’in çalışmaları Psikrometrik Diyagram alanındaki ilk çalışma mıydı? Tabii ki hayır. Daha 1847 yılında Glaisher’ın higrometrik tabloları “Hygrometrical Tables” adı ile yayınlanmış bulunuyordu. Bu tablolar buhar basıncı, barometrik basınç, yaş termometre sıcaklığı , kuru termometre ve yoğuşma sıcaklığı açısından güvenilir bilgiler içeriyordu. Belirli bir sıcaklıkta tam doyma için gerekli buhar miktarı da bu tablolar vasıtasıyla belirlenebiliyordu.

1867’ye gelindiğinde de W. Edson “HYDRODEIK” isimli kuru ve yaş termometre sıcaklıklarını ölçebilen ve üzerine monte edilmiş diyagram vasıtasıyla bağıl nemi belirleyebilen harika bir enstrumanı geliştirmiş ve patentini almıştı.

Bu enstrumanla ölçülen yaş termometre sıcaklığı eğrisi ile kuru termometre eğrisinin kesiştiği noktaya manuel kumandalı buton getirilmekte,butonun üzerinde aşağı-yukarı hareket eden butonun bağlı olduğu kolun ucundaki ok yardımıyla alttaki skalada bağıl nem okunabilmektedir.

1900 yılında da Profesör C.F. Marvin “Psychrometric Tables” isimli çalışmasını yayınlamıştı. Buhar basıncı, bağıl nem, yoğuşma noktası sıcaklığı bu çalışma ile belirlenebiliyordu. Önceki sayfalarda belirtildiği gibi Willis Carrier’in bu çalışmalardan faydalandığı sanılmaktadır.

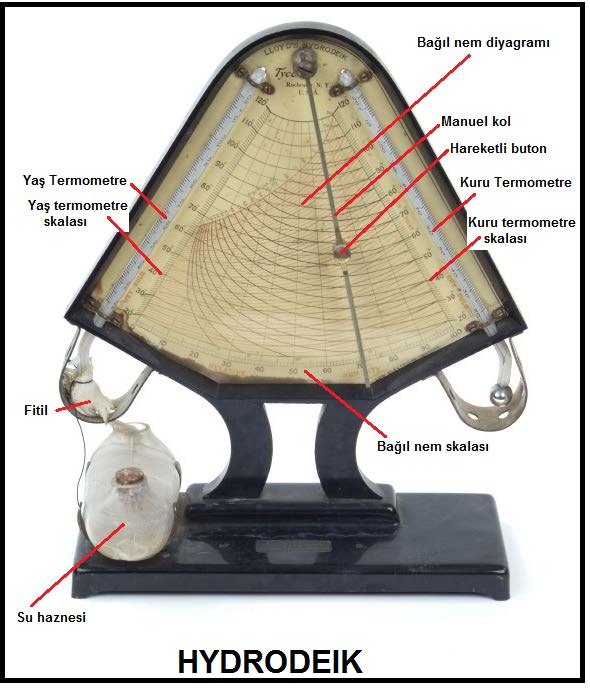
Carrier’in çalışmasından önce elde olan psikrometrik diyagrama benzer çalışmalar Glaisher ve Ferrel’in tablolarından, Hydrodeik enstrumanından ibaretti.  Ancak Carrier’in ilk diyagramı bugün kullanmakta olduğumuzdan bazı farklılıklar içeriyordu.

Willis Carrier ilk diyagramında ordinat olarak su buharının birim ağırlığının beher kuru hava hacmine olan oranını  (grains_WV/ft³_DA) kullanmıştı. Su buharının dansitesinin su buharı basıncına orantılı olması ilk diyagramın yapımını kolaylaştırıyordu.

Carrier’in koordinat seçimi klima uygulamalarının diyagram üzerinde ideale yakın bir şekilde çizilmesini de sağlıyordu. Kuru termometre sıcaklıkları absiste gösterilmiş, sabit sıcaklıklar da düşey çizgilerle belirlenmişti. Yatay çizgiler ise birim hacimdeki su buharını  ağırlık olarak gösteriyordu. Diyagramda “doyma yüzdesi” de %10 ila %100 arasında gösterilmekteydi. Günümüzde “doyma yüzdesi” tabiri artık kullanılmamaktadır. Bunun yerine daha uygun olan “bağıl nem”tabiri kullanılmaktadır.

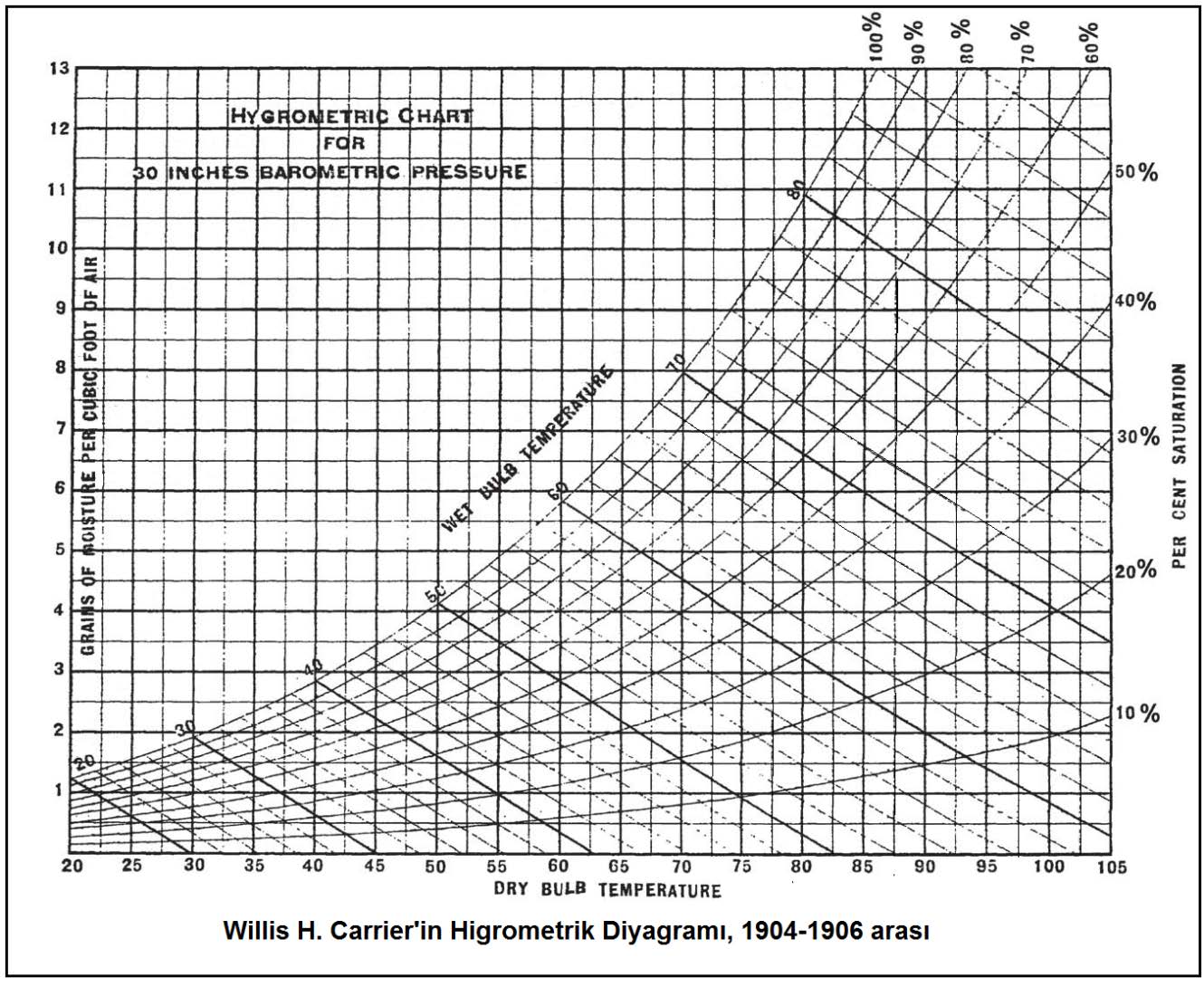
1908 ila 1911 arası ordinatın adı “nem oranı” olarak değiştirilmiş, beher hacimdeki nem miktarı da (lb_VW/ft³_DAveya metrik sistemde  gr_VW/m³_DA) beher kuru hava ağırlığındaki nem miktarı (lb_VW/lb_DAveya metrik sistemde  kg_VW/kg_DA)olarak gösterilmeye başlanmıştı. Ancak “nem oranı” Avrupa’da yaygın olarak “nem miktarı” veya “mutlak nem” olarak ifade edilmektedir. Biz de kitabımızda bundan böyle “mutlak nem” tabirini kullanacağız. Diyagram da  yapılan diğer bir değişiklik te ordinatın soldan sağa taşınmasıdır. Bu arada diyagramın adı da “higrometrik diyagram”dan “Psikrometrik Diyagram”a dönüştürülmüştür. Psikrometrik diyagramın günümüzde kullanılmakta olan hali aşağıda görülmektedir.

Mutlak nem biriminin su buharı ağırlığı bölü birim kuru hava ağırlığı (kg_VW/kg_DA) olarak değiştirilmesi duyulur ısıtma ve duyulur ısıtma proses çizgilerinin yatay doğrular halinde gösterilmesini sağlamıştır. Daha önceki uygulamalarda bu proses çizgileri hafif kurveler halinde gösterilebilmekteydi. Bu değişikliğin sağladığı önemli bir husus ta gizli ısıtma (salt nemlendirme = izotermal nemlendirme) ve gizli soğutma (salt nem giderme = izotermal nem alma) proseslerinin de düşey doğrular halinde gösterilebilmesini sağlamasıdır. Bu iki önemli kazanım sayesinde bir mahallin ısı kazanç ve kayıpları belirlenirken bu yüklerin duyulur ısı ve gizli ısı olarak birbirinden ayrı olarak hesaplanması daha doğru ve daha kolay bir duruma gelmiştir.

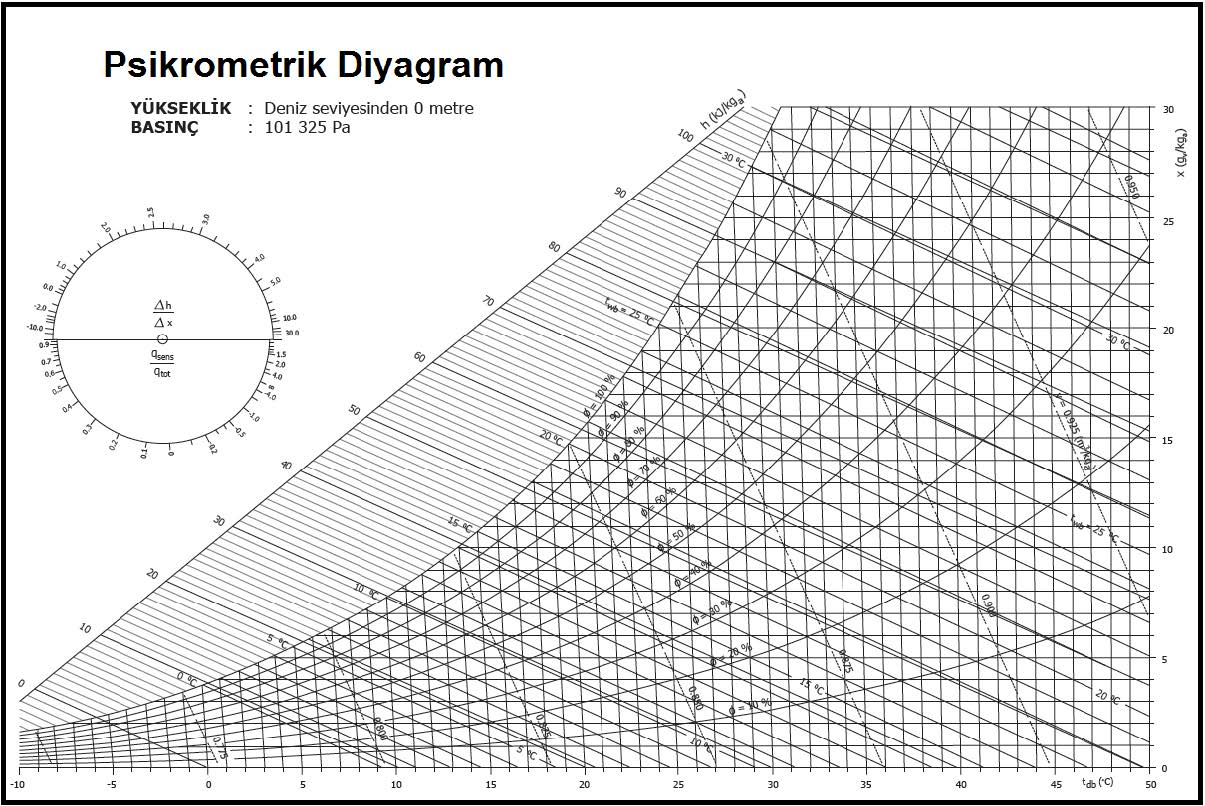
Carrier bu arada adyabatik doyma hacmi (adiabatic saturation chamber) konseptini de geliştirmiştir.

Hazne ideal izoleli olup dışarısıyla ısı alışverişinde bulunmamaktadır (adyabatiktir). Haznenin alt kısmı su ile dolu olup eksilen suya eşit miktar su girişinden tamamlanmaktadır. Doymamış nemli hava hazneye sol taraftan girmekte ve çok yavaş bir hızla sağ taraftan çıkmaktadır. Girişteki hava doymamıştır. Su sathı ile temas ederek geçen hava kısmi buhar basıncı nedeniyle buharlaşmakta ve havaya karışmaktadır. Bunun neticesi olarak sağ taraftan hava doymuş olarak olarak çıkmaktadır. Sıcak havanın sıcaklığı giriş havasından düşüktür. Ancak sistemin antalpisinde bir değişiklik yoktur (bu konu ileride detaylı bir biçimde incelenecektir). Suyun buharlaşması için gereken ısı soğuyan hava tarafından karşılanmaktadır. Bu konsept havanın yıkanması ve bu sayede gerçekleştirilen adyabatik soğutmayı da izah etmektedir.

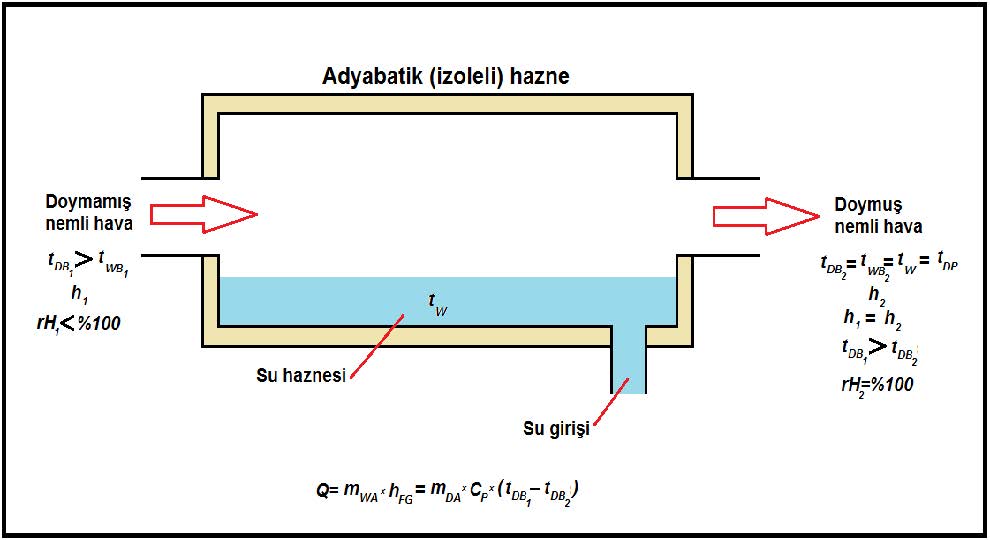
Carrier’in psikrometrik diyagramı gerçekleştirmesini takiben birkaç değişik psikrometrik diyagram çalışmaları da başka bilim adamları tarafından yapılmıştır. Bunların bir kısmını aşağıdaki gibi sıralıyabiliriz:

1. Grosvenor diyagramı…………………….1908
2. Marvin’in psikrometresi………………..1920
3. E.Horton’un diyagramı……………….1921
4. Claud Bulkeley’in diyagramı………….1926
5. M. Ware’in diyagramı………………..1931
6. Lavin ve Sutherland’ın diyagramı…..1931
7. M. Norris’in psikrografı………………1934

Bu daha da uzatmak mümkündür. Carrier’ın haricindeki çalışmaların tamamı 20 adettir. Bunların içinde en önemlisi halen birçok Avrupa ülkesinde kullanılmakta olan Mollier h-x diyagramıdır.

Bu diyagram Prof. Richard Mollier tarafından 1923 yılında gerçekleştirilmiştir. Kullanılan semboller Carrier’in psikrometrik diyagramından farklıdır. Örneğin entalpi “h”, mutlak nem de “x” olarak gösterilmektedir.

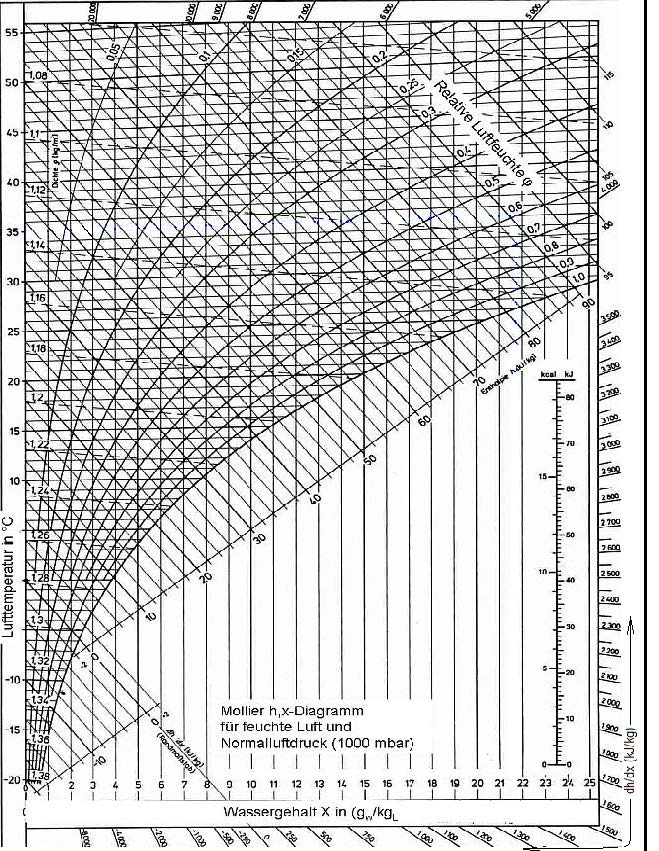
Ancak Mollier diyagramı Carrier’in diyagramında şekil olarak son derece benzemektedir. Sanki Carrier’in diyagramının saat ibresinin ters yönünde döndürülmüş olanının ayna aksi gibidir. Ancak bu benzetmemizden “intihal” gibi bir sonuç çıkarmak son derece yanlış olur. 1863-1935 yılları arasında yaşamış Prof.Dr. Richard Mollier birçok araştırmalar yapmış, çalışmalarını 8 Eylül 1923’de ZVDI’nin 67’nci sayısında yayınlamıştır. Diyagramının temeli antalpi mutlak nem oranını psikrometri dünyasına sunması ve bu oranı diyagramındaki koordinatlardan biri olarak kullanmasıdır. Bu sayede sis oluşumu da incelenebilmektedir.

Psikrometrinin gelişmesi için en çok çaba harcayan kuruluşların başında ASHRAE (American Society of Heating Refrigeration & Air conditioning Engineers Inc. = Amerikan Isıtma, Soğutma ve İklimlendirme Mühendisleri Derneği) gelmektedir. ASHRAE tarafından desteklenen araştırmaların başında Hyland  ile Wexler’in ve Goff ile Gratch’ın yaptığı araştırma ve çalışmalar gelmektedir. Richard Hyland ve Arnold Wexler isimli iki fizikçi ve araştırmacı bilim adamı 1983 yılında iki ASHRAE araştırma projesini tamamlamışlardır. “Nemli Gazların Termodinamik Özelliklerinin Formulasyonu” ve “ Kuru Havanın Termodinamik Özelliklerinin Formulasyonu” isimli bu çalışmalar günümüzün psikrometrisinin temelini oluşturmaktadır.  Günümüzde psikrometrik tablo ve diyagramlar bu araştırmalar sayesinde geliştirilen formül ve değerler esas alınarak yapılmaktadır.