1. KIŞ KLİMASI
1.1. %100 HARİCİ HAVALI KLİMA SANTRALI,YALNIZ ISITMA:
Problem: Toplam hacmi 1200 m3olan bir mahallin ısı kaybı 26 kw’tır. Bu mahallin havasının saatte 8 defa değiştirilmesi ve %100 harici hava kullanılması istenmektedir. Dış hava kış dizayn şartları -10oC, mahal şartları ise 20oC’tır. Klima santralındaki psikrometrik prosesi çizin ve klima santralının tasarımını yapın.
1 kJ = 0.238846 kCal
1 Watt= 0.86 kCal/h
dolayısıyla
1 Watt= 0.86/0.238846 = 3.60065 kJ ; 1kW= 3600.65kJ
Bu durumda yeni “SI” birimlerine göre mahallin ısı yükü:
26×3600.65=93617 kJ/saat’tir.
Mahal için gerekli hava debisi ise:
V=8 x 1200 = 9600 m3/saat bulunur.
Mahal sıcaklığı 20C ve hava debisi 9600 m3/saat olduğuna göre, mahal ısı kaybını karşılamak için gerekli üfleme sıcaklığını bulalım.
Qmahal=V x cpx (1/γ)x (tSA – tRA)
cp=Havanın özgül ısısı…………………………………………….. 1.041 kJ/kg
ϒ =Havanın özgül hacmi (ortalama)..………………………. 0.800 m3/kg
Değerleri yerine koyduğumuzda:
93617= 9600 x 1.041 x( 1/0.800)x(tSA – 20)
tSA = 27.49oC ≈ 28oC bulunur.
Dış havanın mahal şartlarına kadar ısıtılması için gerekli ısı miktarı:
Qdış hava=V x cpx (1/γ)x (tRA – tOA)
Qdış hava=9600 x 1.041 x (1/0.800)x (20 + 10)=374769 kJ/saat
Klima santralındaki ısıtıcı bataryanın toplam yükü ise:
ΣQ= Qmahal + Qdış hava
ΣQ= 93617 + 374760 = 468377 kJ/saat (= 130.08 kW)
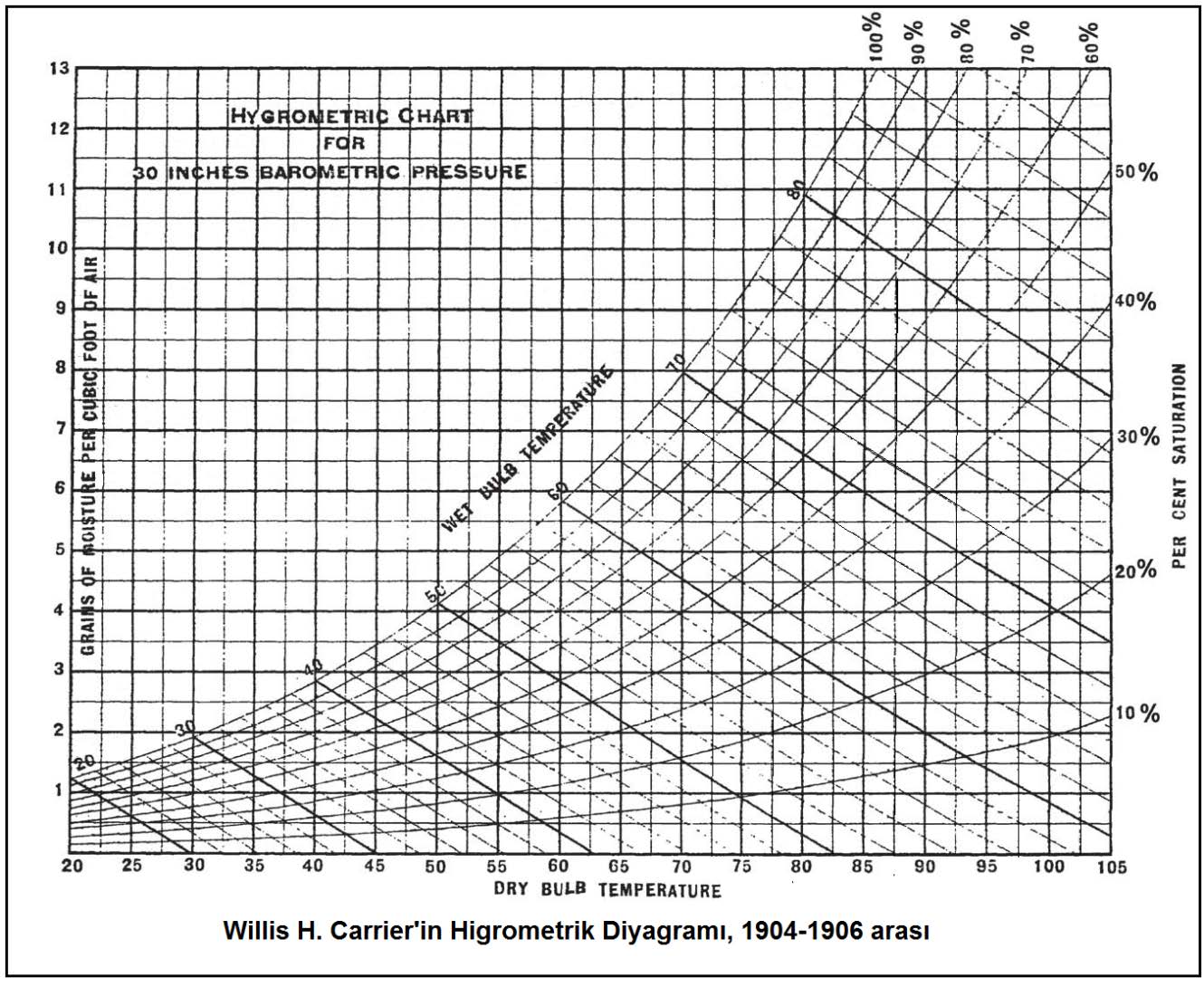
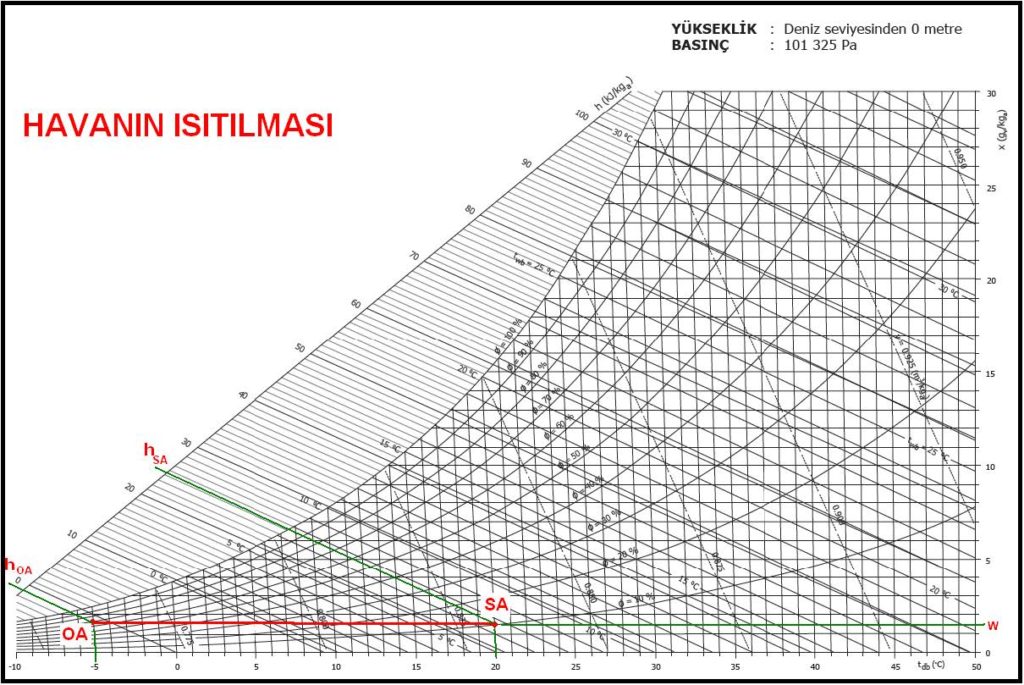
Bu prosesi psikrometrik diyagram üzerinde gösterelim.
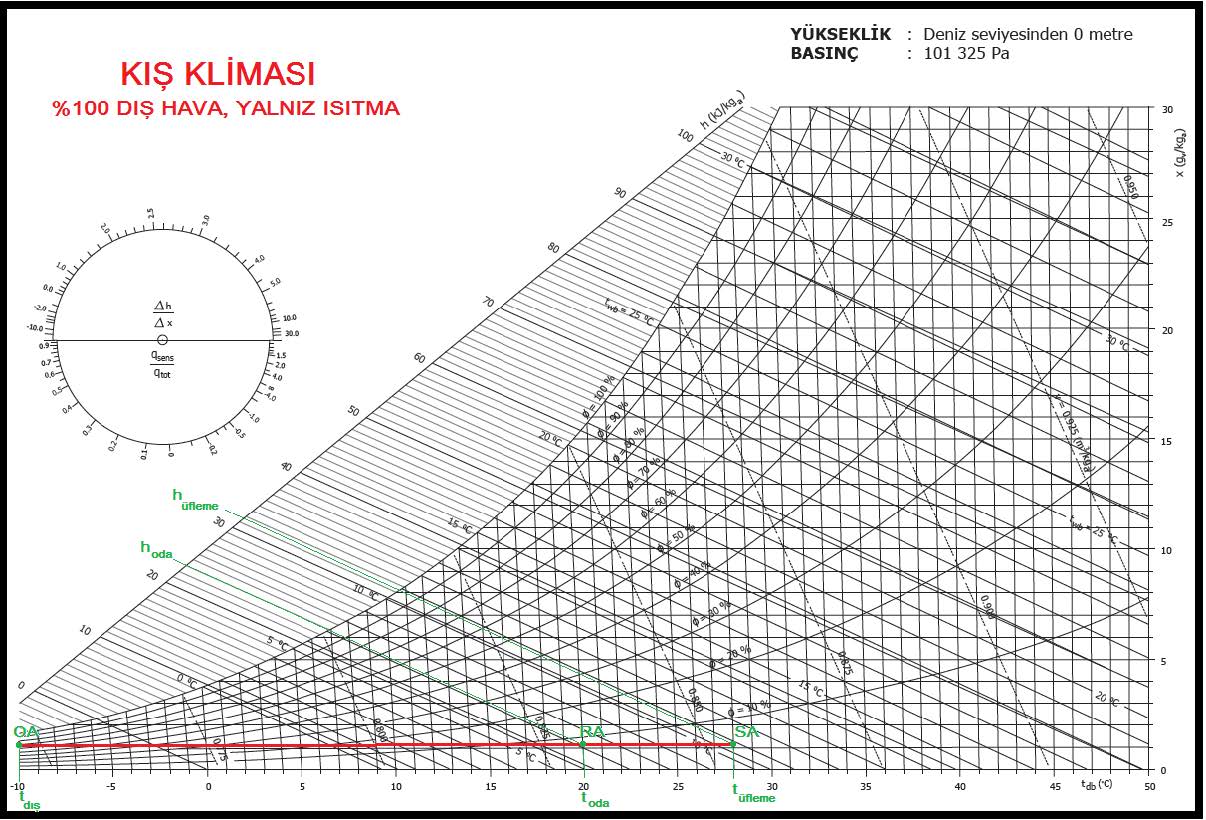
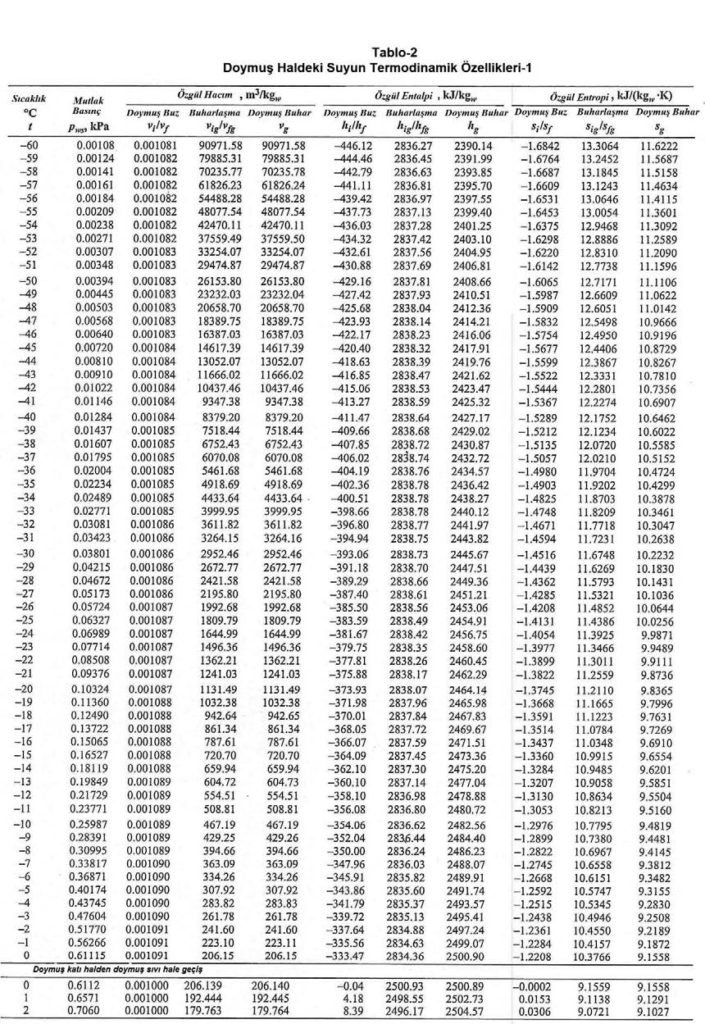
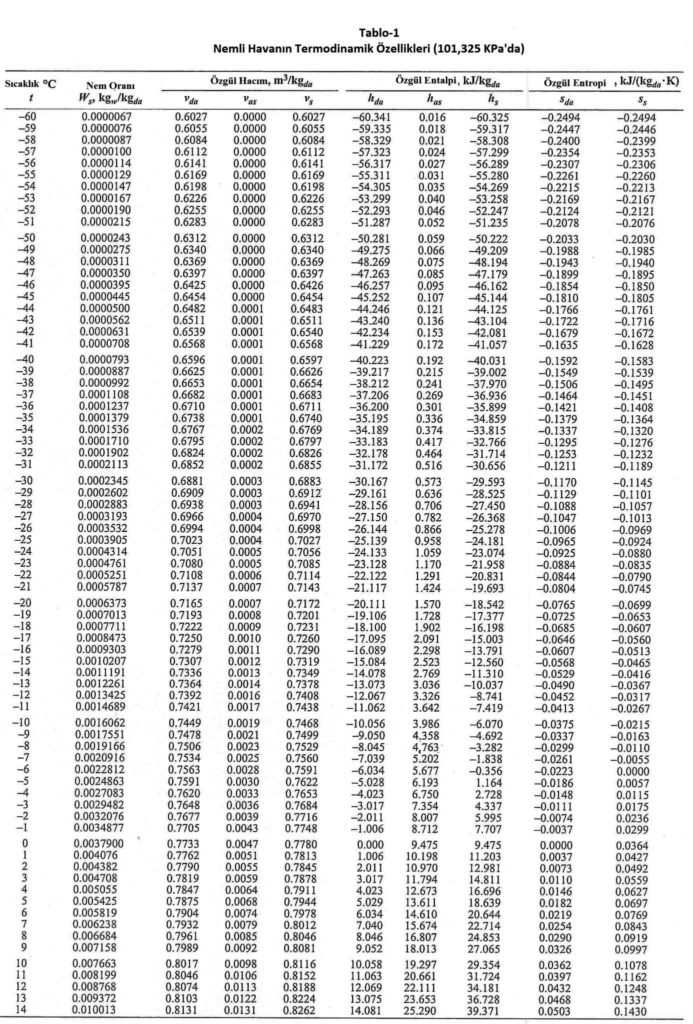
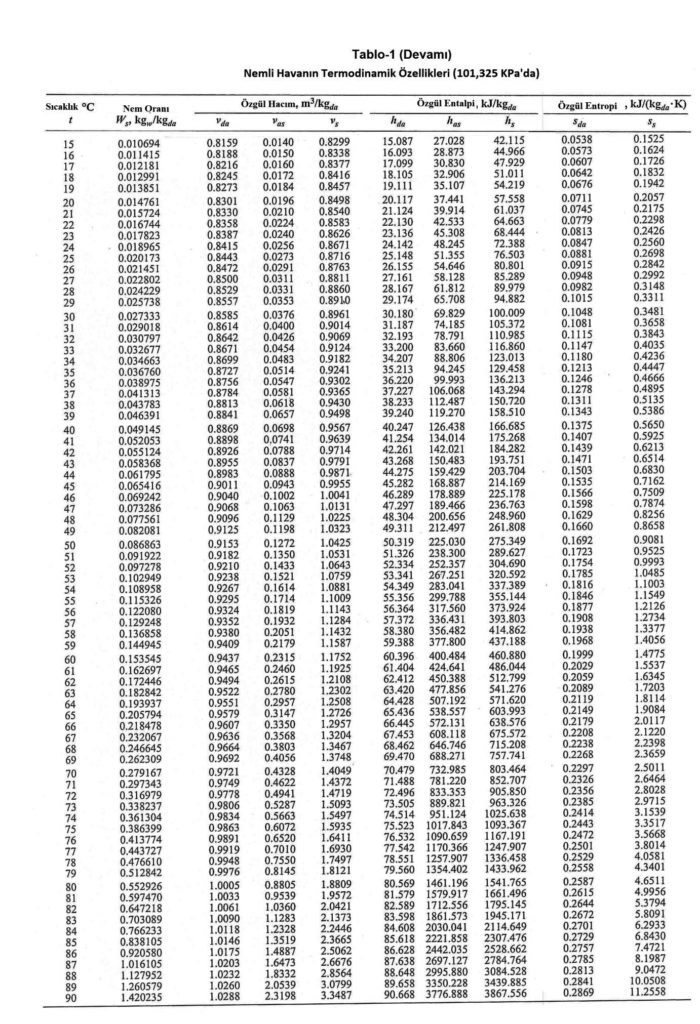
hOA= -7.2585 kJ/kg …………………..(bkz. Psikrometri-I, sayfa 132, 8-Tablo ve diyagramlar)
γOA= 0.7469 m3/kg…………………… (bkz. Psikrometri-I, sayfa 132, 8-Tablo ve diyagramlar)
hRA = 23.00 kJ/kg …………………… (Yukarıdaki psikrometrik diyagramdan)
γRA = 0.8305 m3/kg h…………………(bkz. Psikrometri-I, sayfa 133, 8-Tablo ve diyagramlar)
hSA= 31.60 kJ/kg …………………… (Yukarıdaki psikrometrik diyagramdan)
γSA= 0.8565 m3/kg h…………………(bkz. Psikrometri-I, sayfa 133, 8-Tablo ve diyagramlar)
Önceki hesabımızda olduğu gibi “ϒ”değerini 0.800 m3/kg kabul ederek hesabımızı yapabiliriz.
Qdış hava=V x (1/γ)x (hRA– hOA)
Qmahal =V x (1/γ)x (hSA – hRA)
ΣQ= Qmahal + Qdış hava
Bu duruma göre:
Qdış hava=V x (1/γ)x (hRA– hOA)
Qdış hava=9600 x (1/0.800)x (23.00+7.2585)
Qdış hava=363 102 kJ/saat
Qmahal =V x (1/γ)x (hSA – hRA)
Qmahal =9600 x (1/0.800)x (31.60– 23.00)
Qmahal =103200 kJ/saat
ΣQ= Qmahal + Qdış hava
ΣQ= 103200+ 363102 = 466302 kJ/saat= 129.50 kW
İki hesaplama metodu arasındaki farklılık havanın özgül hacminin sabit kabul edilmesinden ve psikrometrik diyagramda yapılan okuma hatalarından kaynaklanmaktadır. Fark %1’den azdır ve ihmal edilebilir. Çok hassas bir hesap için her sıcaklık için özgül hacimleri de dikkate almak gerekir, söyleki:
Qdış hava=V x (hRAx(1/γRA)– hOAx(1/γOA))
Qmahal =V x (hSAx(1/γSA)– hRAx(1/γRA))
ΣQ= Qmahal + Qdış hava
Qdış hava=9600 x (23.00x(1/0.8305)+ 7.2585x(1/0.7469))=359158 kJ/saat
Qmahal =9600 x (31.60x(1/0.8565)– 23.00x(1/0.8305)) = 88322 kJ/saat
ΣQ = 359158 + 88322 = 447480 kJ/saat = 124.3 kW
Son yapılan hesap üç metod içinde en hassas olanıdır. Ancak aradaki fark %5’in altındadır. Bu nedenle konfor şartları içinde yapılacak hesaplarda her üç metod da uygulanabilir. Tercih hesap yapan kişiye aittir. Ancak çok yüksek sıcaklıklar (t>50oC) ve çok düşük sıcaklıklar
(t<-15oC) esas alınarak hesap yapılacaksa muhakkak her sıcaklığa ait özgül hacim değerleri dikkate alınmalıdır.
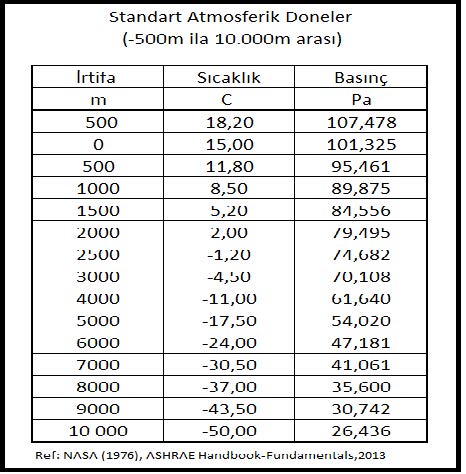
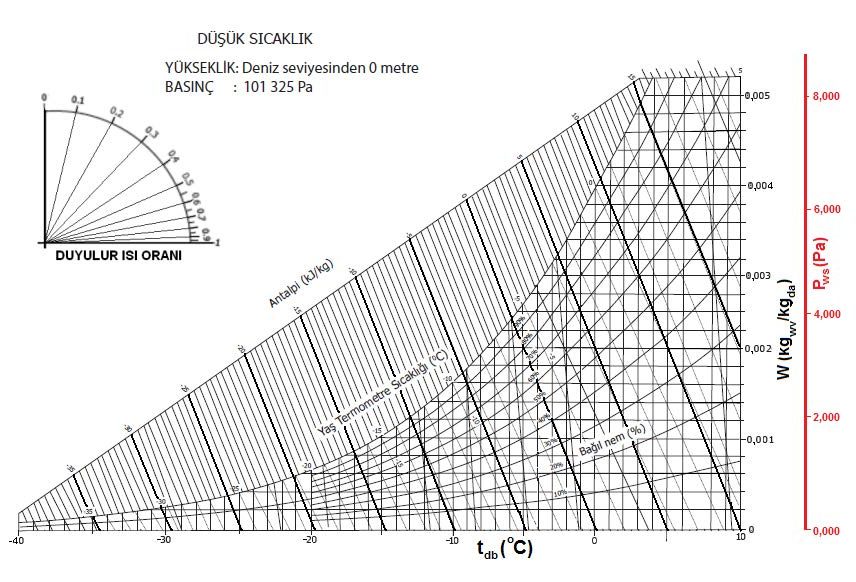
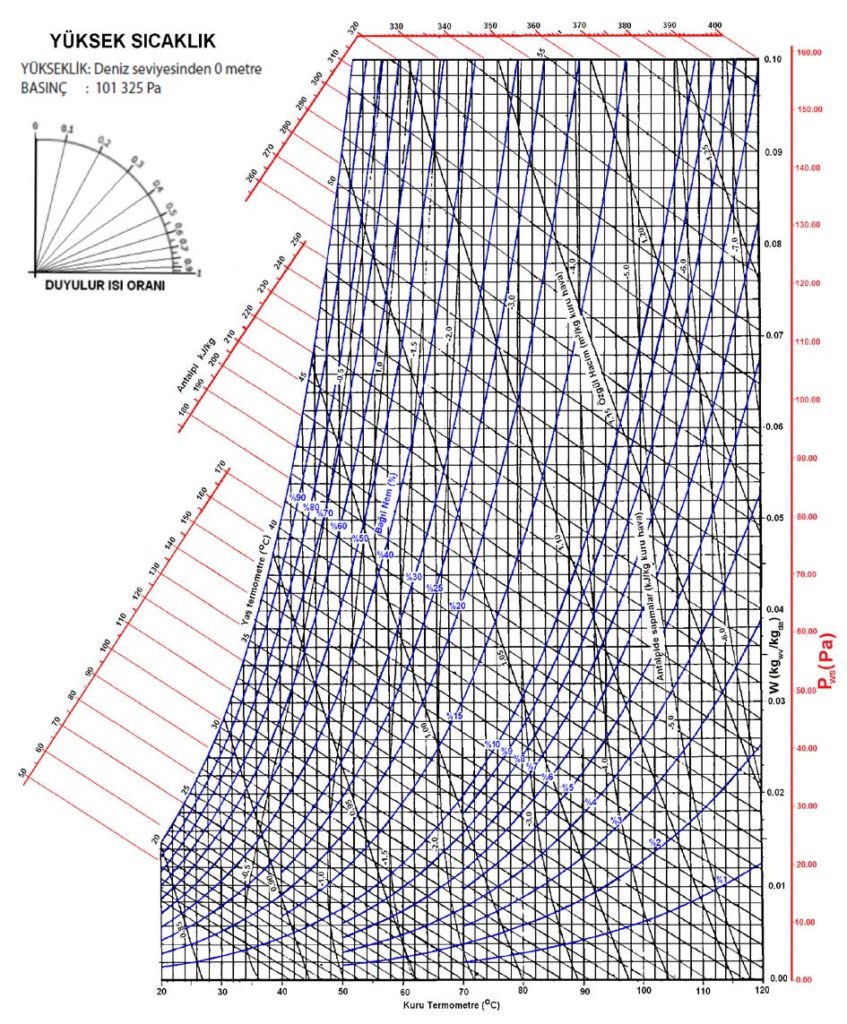
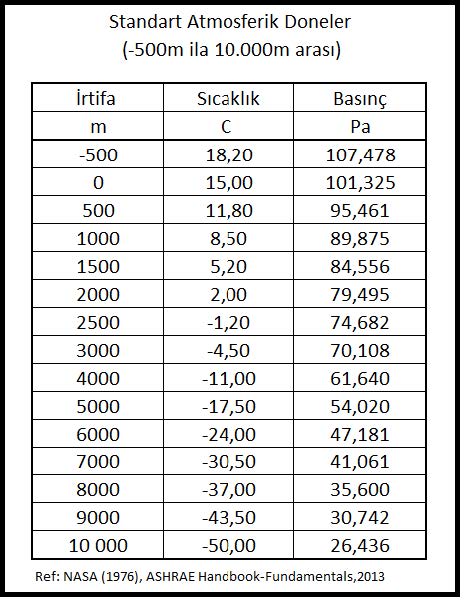
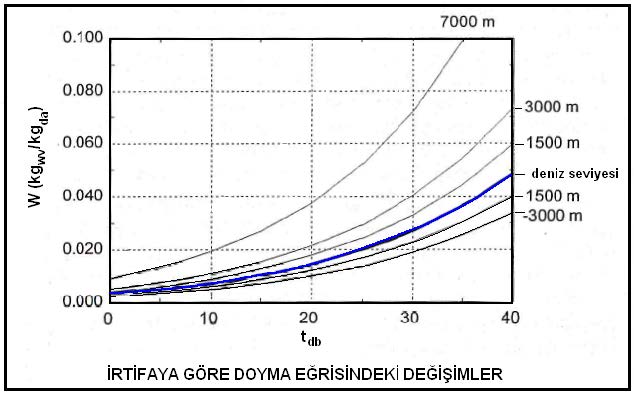
Dikkate alınması gereken diğer bir husus ta irtifa (deniz seviyesinden yükseklik)tir. İrtifa arttıkça atmosferik basınç azalacağından ve bu nedenle havanın özgül hacmi artacağından toplam ısı yüklerinde değişiklikler olacaktır. Be nedenle hesaba esas olan ortama en yakın psikrometrik diyagram ve tablolar kullanılmalıdır.
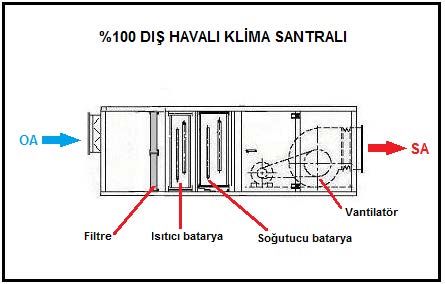
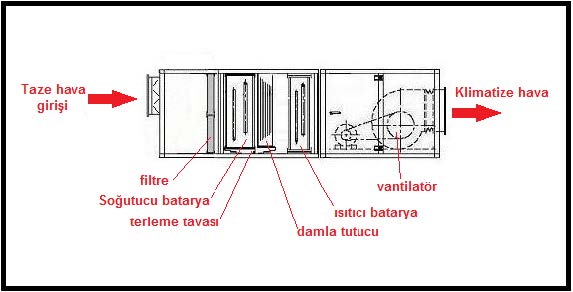
Aşağıdaki resimde, probleme konu olan,%100 harici havalı klima santralı görülmektedir.
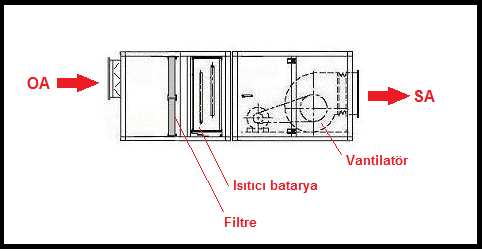
1.2. KARIŞIM HAVALI KLİMA SANTRALI, YALNIZ ISITMA:
Problem: Toplam hacmi 1200 m3olan bir mahallin ısı kaybı 26 kw’tır. Bu mahallin havasının saatte 8 defa değiştirilmesi ve %100 harici hava kullanılması istenmektedir. Dış hava kış dizayn şartları -10oC, mahal şartları ise 20oC, bağıl nemi %35’dir.Mahalde 32 kişi bulunmaktadır. Kişi başına 60 m3/saat taze hava miktarı esas alınarak klima santralındaki psikrometrik prosesi çizin ve klima santralının tasarımını yapın.
Vtoplam=1200 x 8 = 9600 m3/saat
Vdış = 32 kişi x 60 m3/saat.kişi = 1920 m3/saat
Dış hava oranı= 1920 / 9600 = 0.20 =%20
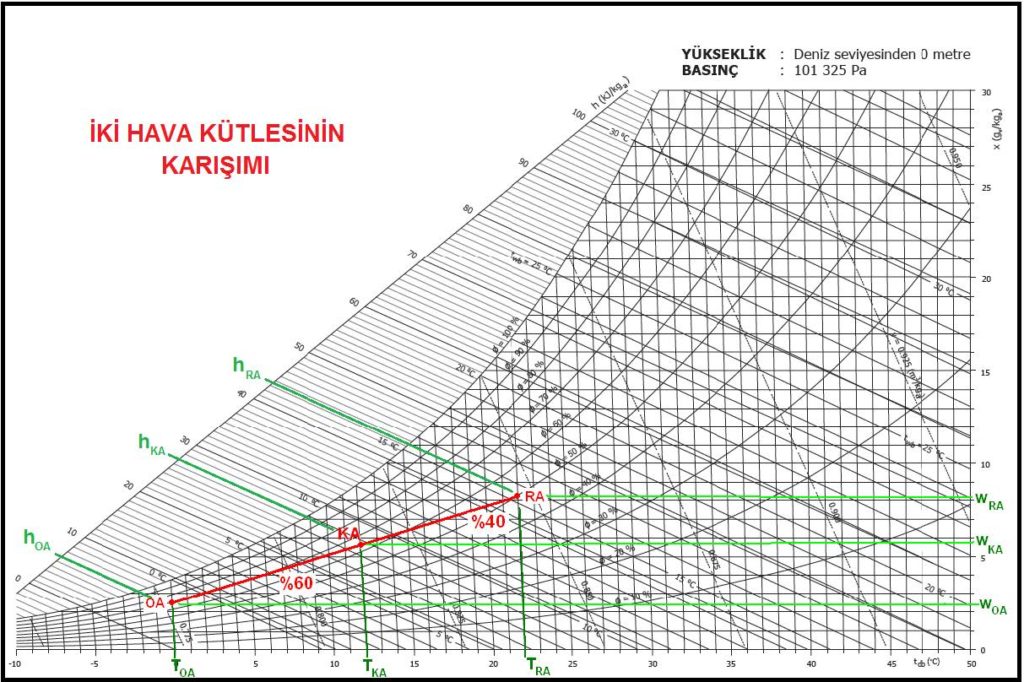
Psikrometrik diyagram üzerine dış hava-mahal havası karışımı işleyip prosesimizi belirleyelim.
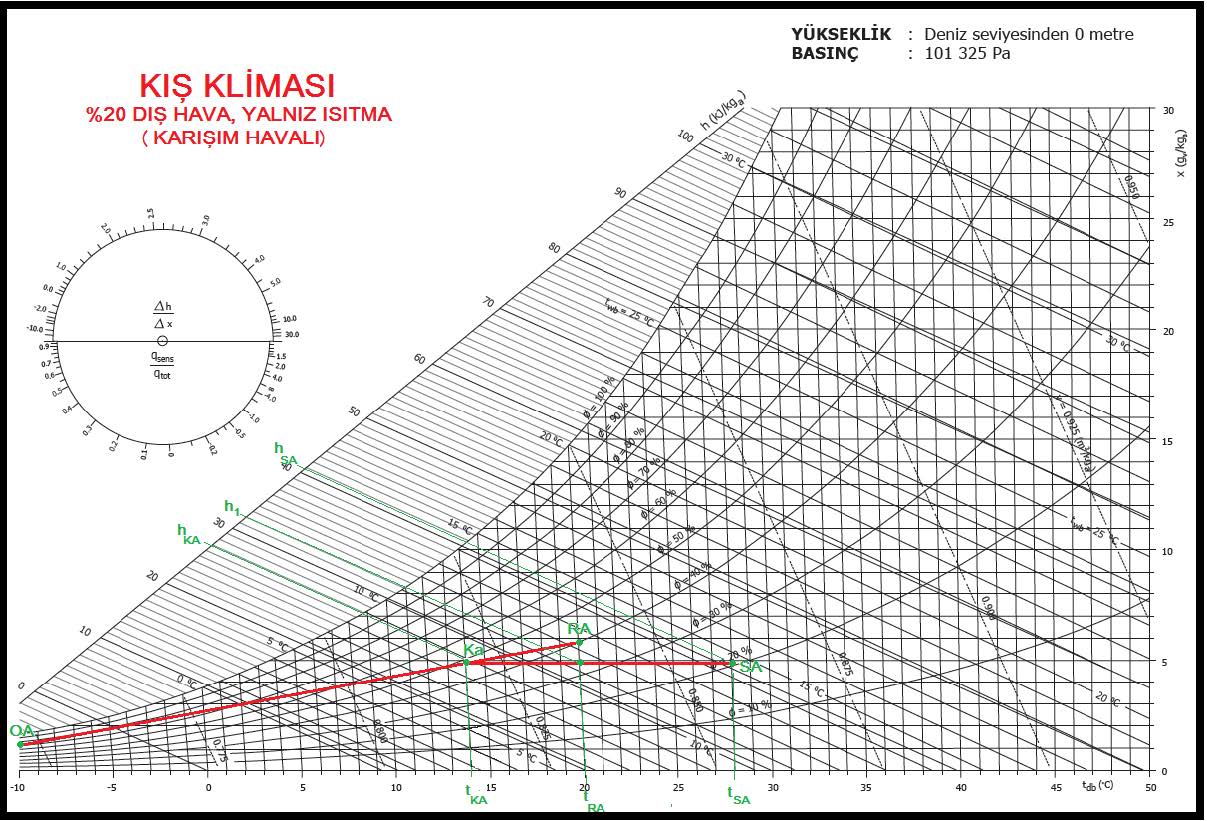
“Ka” olarak gösterilen konum %20 dış hava ile %80 dönüş (resirküle) havanın karıştığı konumdur. “OA-RA” hattı iç hava ile dış havanın karışım prosesini göstermektedir. Analitik olarak çözüm yaptığımızda “OA-RA” uzunluğunun %20’sine eşit olan mesafe “RA” tarafından işaretlenir. Bu nokta “Ka”, iki havanın karışım noktasıdır.
“RA” mahal şartlarını, “SA” da üfleme havasının şartlarını simgelemektedir. Bir önceki örnekte olduğu gibi “tSA” ile “tRA” arasındaki ısıtma prosesi mahal ısı kaybını karşılamak için yapılan prosestir. “tKA” ile “tSA” arasındaki proses ise dış havadan kaynaklanan ısıtma prosesidir. 20oC kuru termometre sıcaklığındaki hava -10oC kuru termometre sıcaklığındaki dış hava ile yukarıda belirtilen şartlarda karışarak “Ka” meydana gelmiştir. “Ka”nın kuru termometre sıcaklığı 14oC’tır. Dolayısıyla karışım nedeniyle 14oC’a kadar soğuyan karışım havası mahal kuru termometre sıcaklığı olan 20oC’a kadar ısıtılacak ve bu sayede dış havanın yarattığı soğuma efekti giderilecek, bilahare hava üfleme sıcaklığına kadar ısıtılmak suretiyle mahal ısı kaybı karşılanmış olacaktır. Bu uygulamada %100 harici hava yerine mahaldeki insan sayısı dikkate alınarak belirli bir oranda (%20) harici hava kullanımına gidilmiş ve önemli ölçüde enerji tasarrufu yapılmıştır.
Mahal ısı yükünün karşılanması “1.0” daki problemde olduğu gibidir. Oradaki hesabı aynen buraya alıyoruz.
Yeni “SI” birimlerine göre mahallin ısı yükü:
26×3600.65=93617 kJ/saat’tir.
Mahal için gerekli hava debisi ise:
V=8 x 1200 = 9600 m3/saat’tir.
Mahal sıcaklığı 20oC ve hava debisi 9600 m3/saat olduğuna göre, mahal ısı kaybını karşılamak için gerekli üfleme sıcaklığını bulalım.
Qmahal=V x cpx (1/γ)x (tSA – tRA)
cp=Havanın özgül ısısı…………………………………………….. 1.041 kJ/kg
ϒ =Havanın özgül hacmi (ortalama)..………………………. 0.800 m3/kg
Değerleri yerine koyduğumuzda:
93617= 9600 x 1.041 x( 1/0.800)x(tSA – 20)
tSA = 27.49oC ≈ 28oC bulunur.
Karışım havasının mahal şartlarına kadar ısıtılması için gerekli ısı miktarı:
Qdış hava=V x cpx (1/γ)x (tRA – tOA)
Qdış hava=9600 x 1.041 x (1/0.800)x (20 – 14)=74952 kJ/saat
Klima santralındaki ısıtıcı bataryanın toplam yükü ise:
ΣQ= Qmahal + Qdış hava
ΣQ= 93617 + 74952 = 168569 kJ/saat (= 48.62 kW)
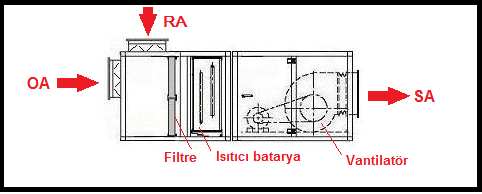
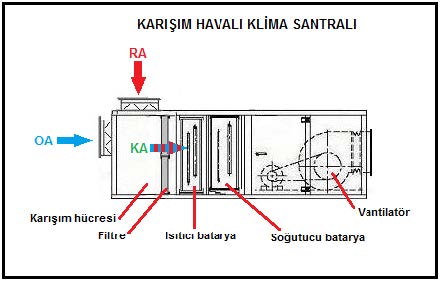
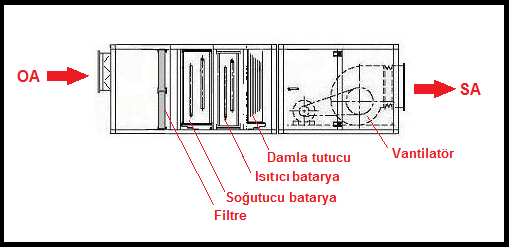
Karışım havalı, yalnız ısıtıcı bataryalı klima santralının resmi aşağıdadır. Bu uygulamada klima santralının iki hava girişi bulunmaktadır. Bunlardan biri “RA” olarak gösterilen dönüş havası, diğeri de “OA” olarak gösterilen dış havadır. Bu uygulamada her iki hava girişi üzerinde debi reğlaj damperleri vardır. Bu damperler sayesinde karışım oranı belirlenir ve sabitlenir. Ancak
Dış hava sıcaklığının 0oC’ın altında olması nedeniyle, sistem karışım havasıyla da çalışsa bir donma riski vardır. Bu nedenle damperlerin üzerine iki konumlu servomotorlar (damper motorları) konmasında yarar vardır. Donma konusu klima santralları otomatik kontrolunda detaylı bir biçimde ele alınacaktır.
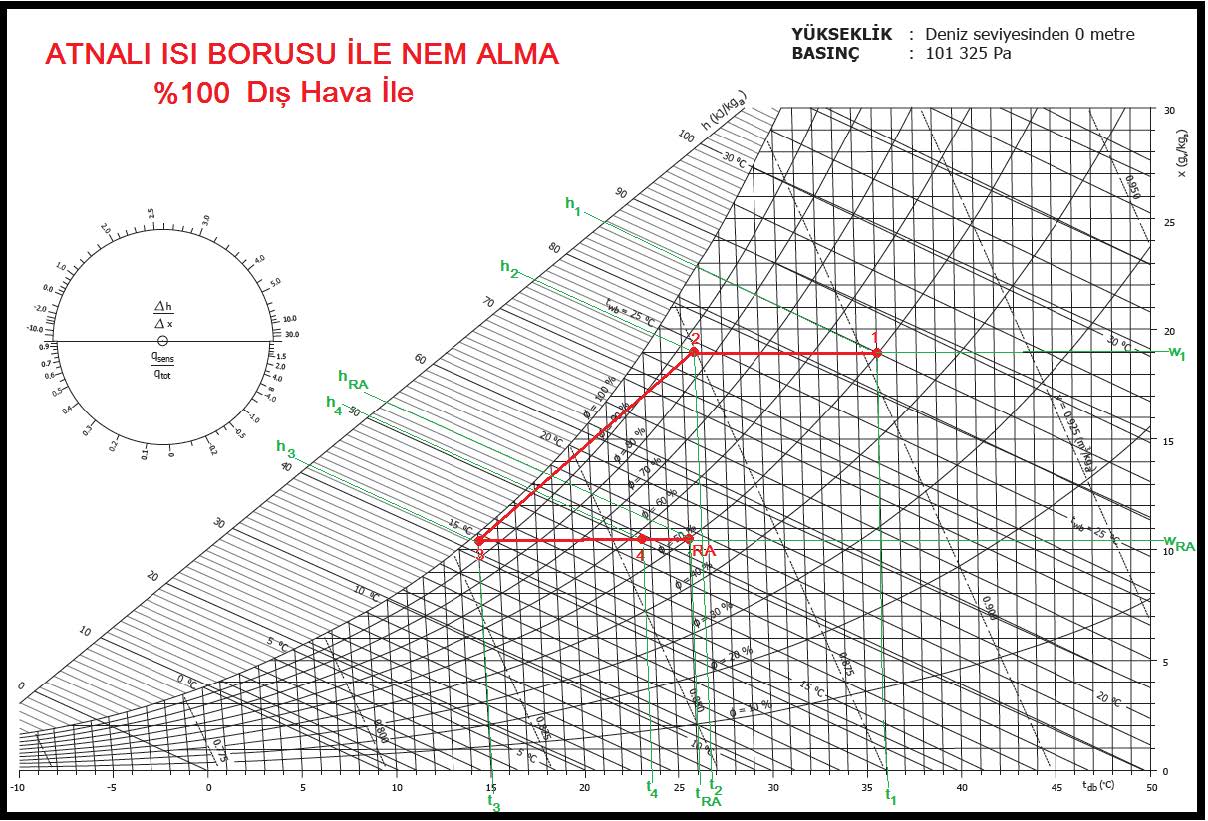
1.3. %100 DIŞ HAVALI KLİMA SANTRALI, ISITMA VE HAVA YIKAYICI İLE NEMLENDİRME
Problem: Toplam hacmi 1200 m3olan bir mahallin ısı kaybı 26 kw’tır. Bu mahallin havasının saatte 8 defa değiştirilmesi ve %100 harici hava kullanılması istenmektedir. Dış hava kış dizayn şartları -10oCKT,%70 rH, mahal şartları ise 20oCKT, %50 rH’tır.Klima santralında hava yıkayıcı ile nemlendirme yapılıp, üfleme havasının mutlak neminin oda şartlarına çıkarılması istenmektedir. Klima santralındaki psikrometrik prosesi çizin ve klima santralının tasarımını yapın.
1 kJ = 0.238846 kCal
1 Watt= 0.86 kCal/h
dolayısıyla
1 Watt= 0.86/0.238846 = 3.60065 kJ ; 1kW= 3600.65kJ
Bu durumda yeni “SI” birimlerine göre mahallin ısı yükü:
26×3600.65=93617 kJ/saat’tir.
Mahal için gerekli hava debisi ise:
V=8 x 1200 = 9600 m3/saat bulunur.
Mahal sıcaklığı 20oC ve hava debisi 9600 m3/saat olduğuna göre, mahal ısı kaybını karşılamak için gerekli üfleme sıcaklığını bulalım.
Qmahal=V x cpx (1/γ)x (tSA – tRA)
cp=Havanın özgül ısısı…………………………………………….. 1.041 kJ/kg
ϒ =Havanın özgül hacmi (ortalama)..………………………. 0.800 m3/kg
Değerleri yerine koyduğumuzda:
93617= 9600 x 1.041 x( 1/0.800)x(tSA – 20)
tSA = 27.49oC ≈ 28oC bulunur. Bu sıcaklık psikrometrik diyagramda “SA” olarak gösterilmektedir.
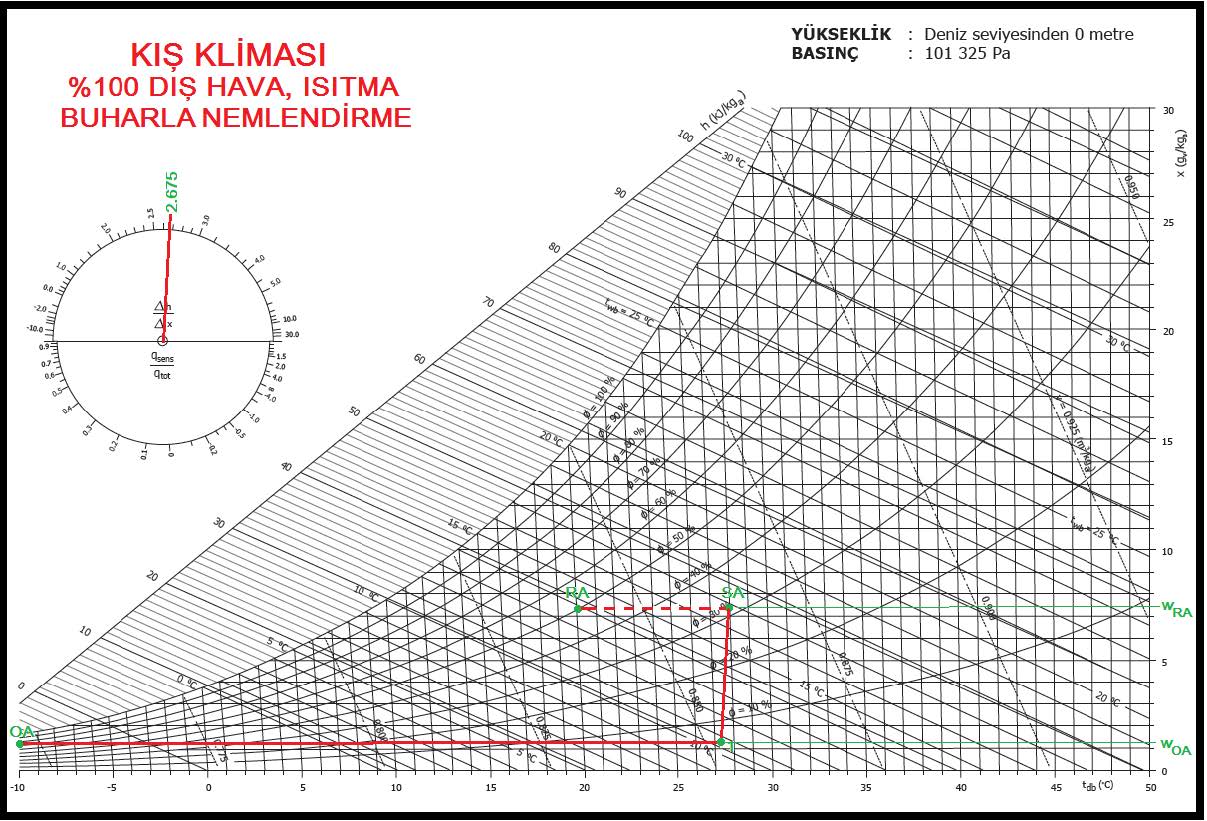
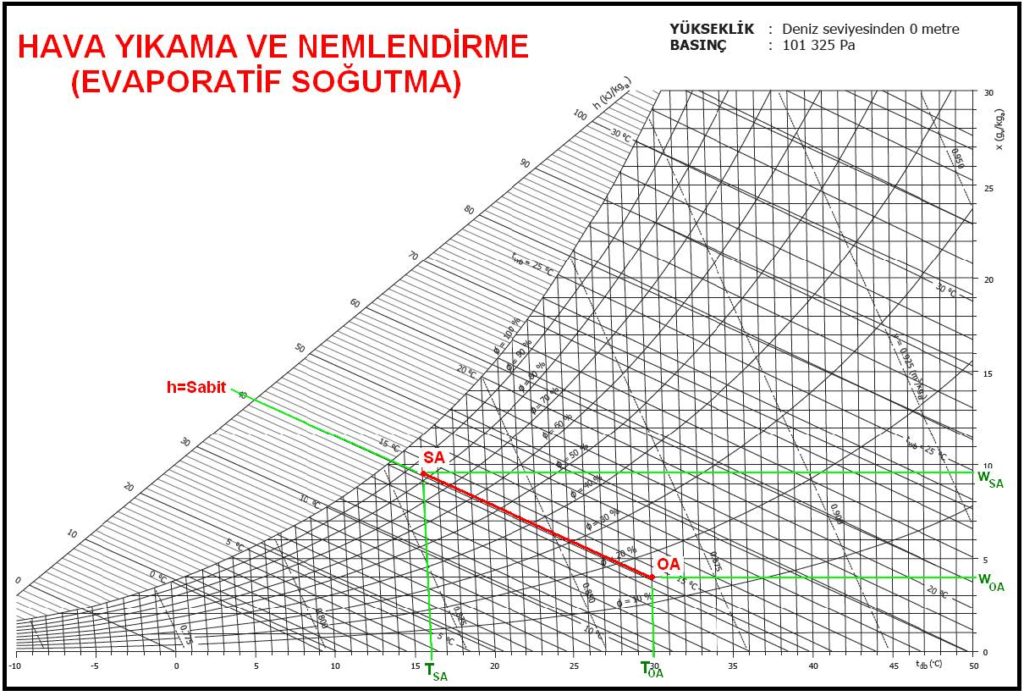
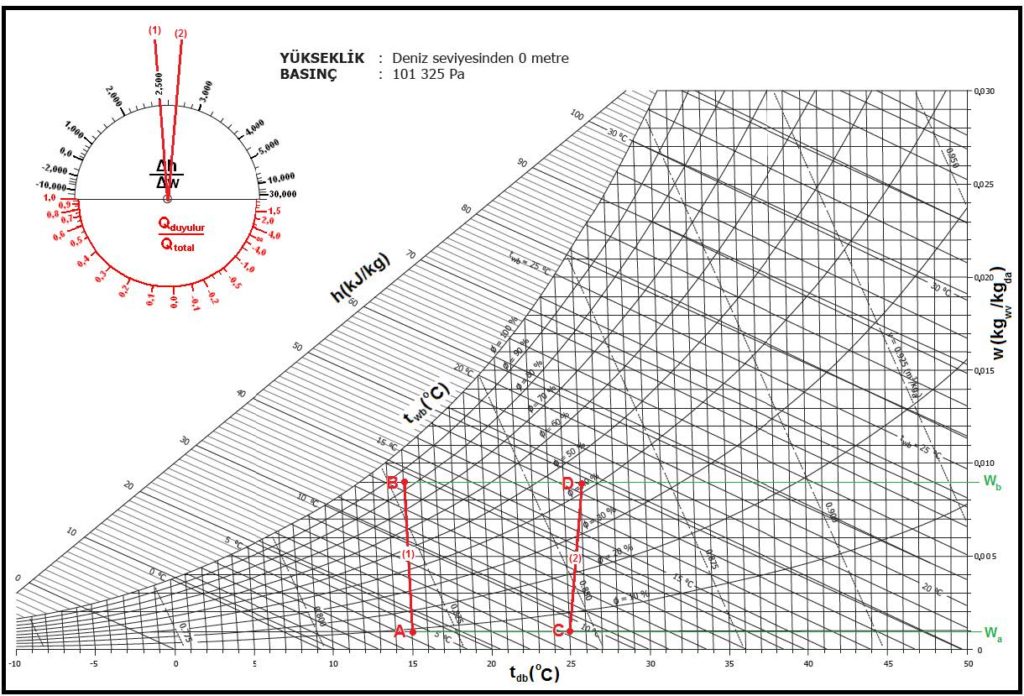
Psikrometrik proses ise aşağıda gösterildiği gibidir.
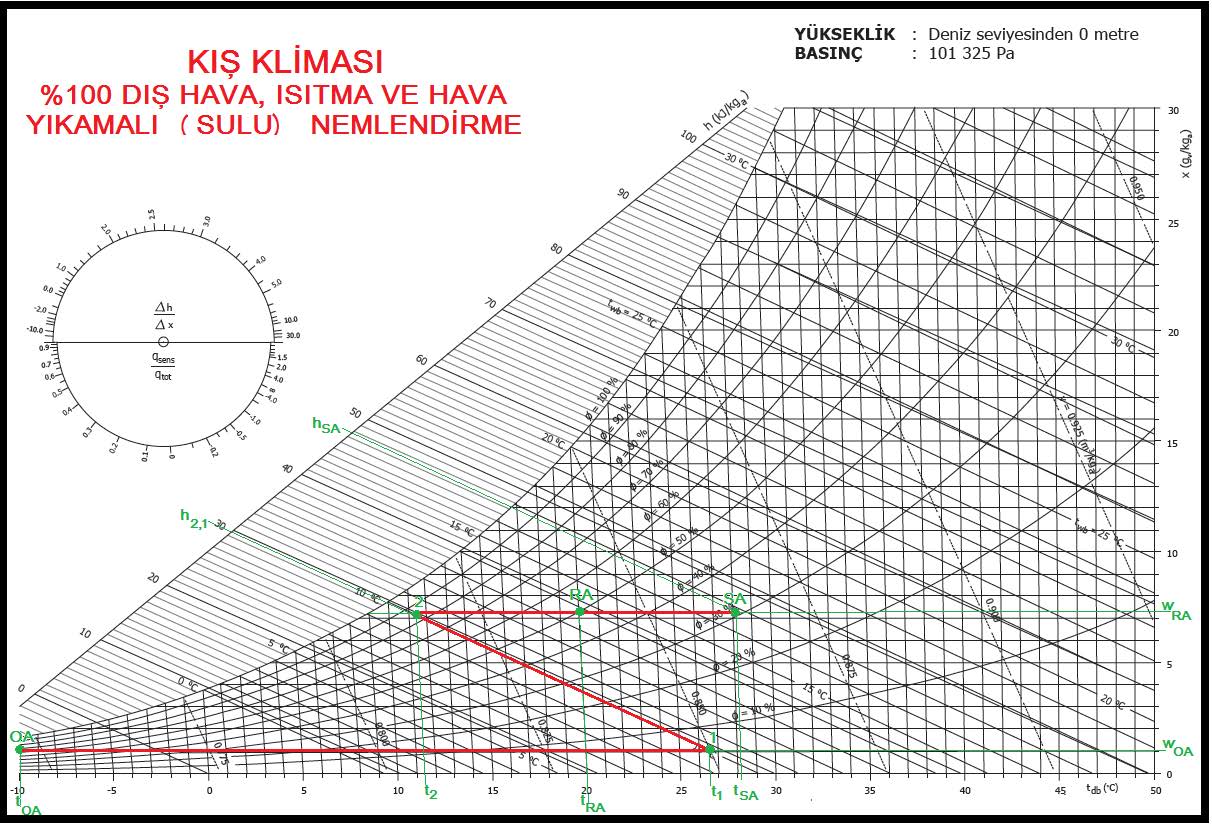
Bu prosesle ilgili önemli hususları aşağıdaki gibi belirtebiliriz:
- Nemlendirme neticesinde “wOA” olan dış havanın mutlak nemi “wRA”seviyesine çıkarılacaktır.
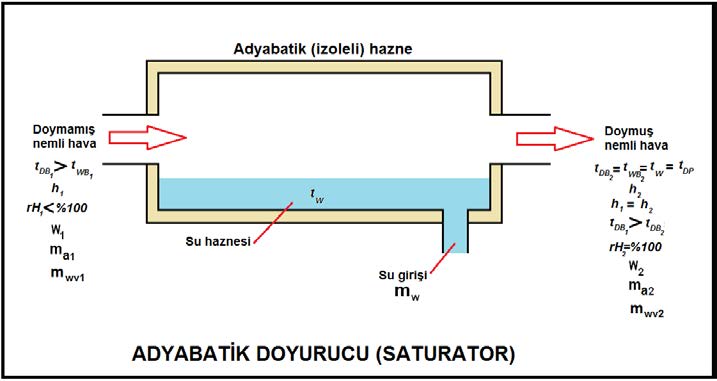
- Bu işlem için hava yıkayıcısı kullanılacaktır. Havanın içine su püskürtülme ile neminin arttırılması işlemi adyabatik bir işlemdir, sabit entalpide cereyan eder. Buharlaşan su gerekli buharlaşma enerjisini havadan alacak ve bunun neticesi bir soğuma meydana gelecektir.
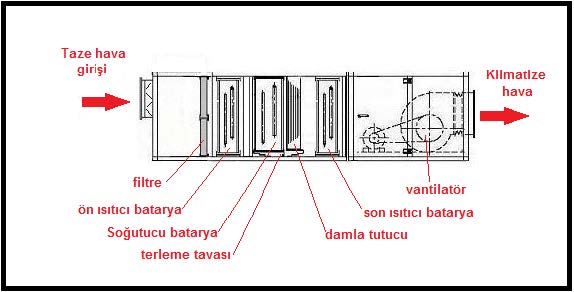
- Evaporatif işlem neticesi havanın soğumasını karşılayabilmek, aynı zamanda mahal ısı ihtiyacını karşılayabilmek için ikinci bir ısıtıcıya gerek vardır. Bu nedenle klima santralında “ön ısıtıcı” ve “son ısıtıcı” olarak adlandırılan iki ısıtıcı batarya bulunacaktır.
“OA-1” prosesi dış havanın ön ısıtıcıda ısıtılması işlemidir. “1-2” prosesi ise havanın içine su püskürtülmesi neticesi mutlak neminin arttırılması işlemidir. “2-SA” prosesi ise havanın tekrar ısıtılması işlemidir. Bu işlem hem evaporatif soğumayı karşılamakta, hem de mahal ısı kaybı için gerekli enerjiyi üfleme havasına ilave etmektedir.
Şimdi ön sıtıcı ve son ısıtıcı büyüklüklerini belirleyelim.
cp=Havanın özgül ısısı ………………………………………………. 1.041 kJ/kg
γ=Havanın özgül hacmi (ortalama)..………………………. 0.800 m3/kg
hOA= -7.2585 kJ/kg …………………..(bkz. Psikrometri-I, sayfa 132, 8-Tablo ve diyagramlar)
h1 = 29.80 kJ/kg …………………… (Yukarıdaki psikrometrik diyagramdan)
h2 = 29.80 kJ/kg …………………… (Yukarıdaki psikrometrik diyagramdan)
hSA = 46.70 kJ/kg …………………… (Yukarıdaki psikrometrik diyagramdan)
Ön ısıtıcı büyüklüğü:
Qön ısıtıcı=V x (1/γ)x (h1– hOA)
Qön ısıtıcı=9600 x (1/0.800)x (29.80+7.2585)
Qön ısıtıcı=444 702 kJ/saat
Qön ısıtıcı =123,50 kW
Son ısıtıcı büyüklüğü:
Qson ısıtıcı=V x (1/γ)x (h1– hOA)
Qson ısıtıcı=9600 x (1/0.800)x (46.70– 29.80)
Qson ısıtıcı= 202 800 kJ/saat
Qson ısıtıcı = 56.32 kW
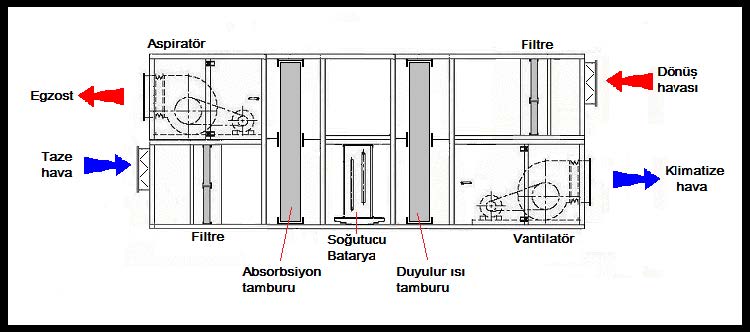
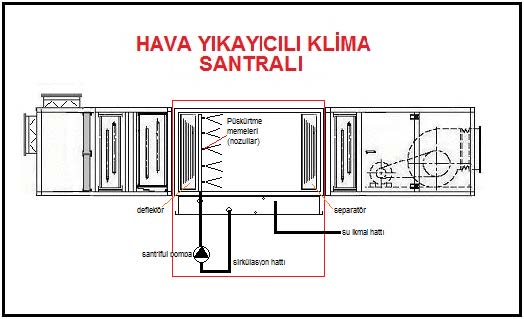
Nemlendirici için bir hesaba gerek yoktur. Hava yıkayıcılı sistemlerde genel tatbikat 1 m3/saat hava için 0.8 ila 1 lt/saat suyun püskürtülmesi tarzındadır.Nozul basıncı da seçilen nozul tipine bağlı olup genelde 15mSS ila 30mSS arasındadır. Dolgu tipi nemlendirici (matt type humidifier) kullanılıcaksa üretici firma değerleri esas alınmalıdır. Klima santralının şematik çizimi aşağıdadır.
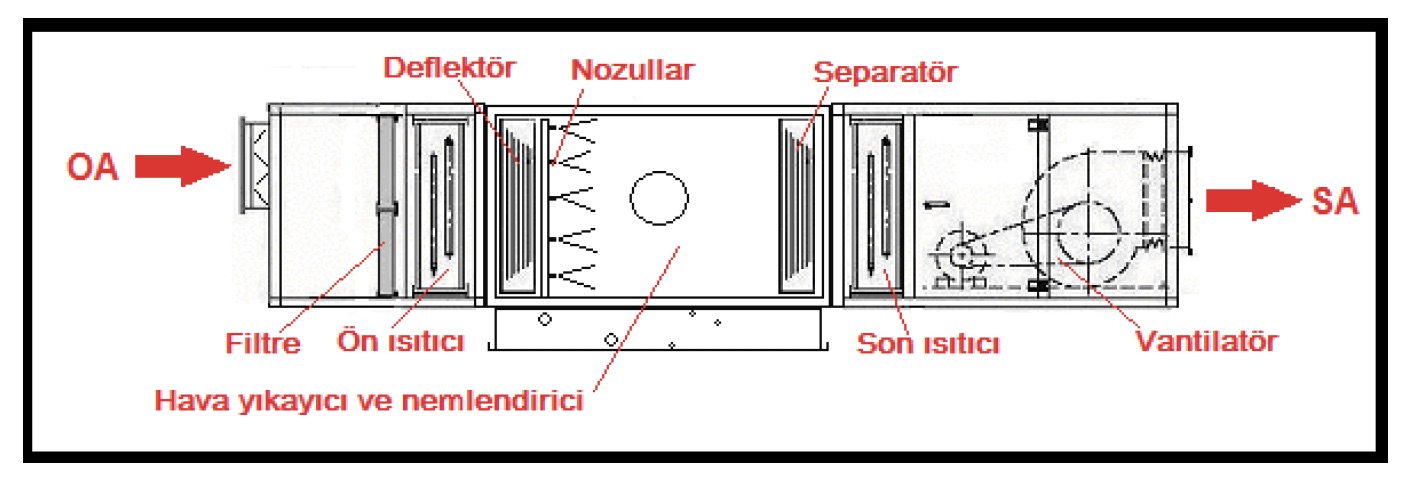
Şekilde görülen “deflektör” havaya yön verici görevini yerine getirmektedir. “Separatör” ise havaya karışmamış su damlacıklarının sürüklenmesine mani olmaktadır.
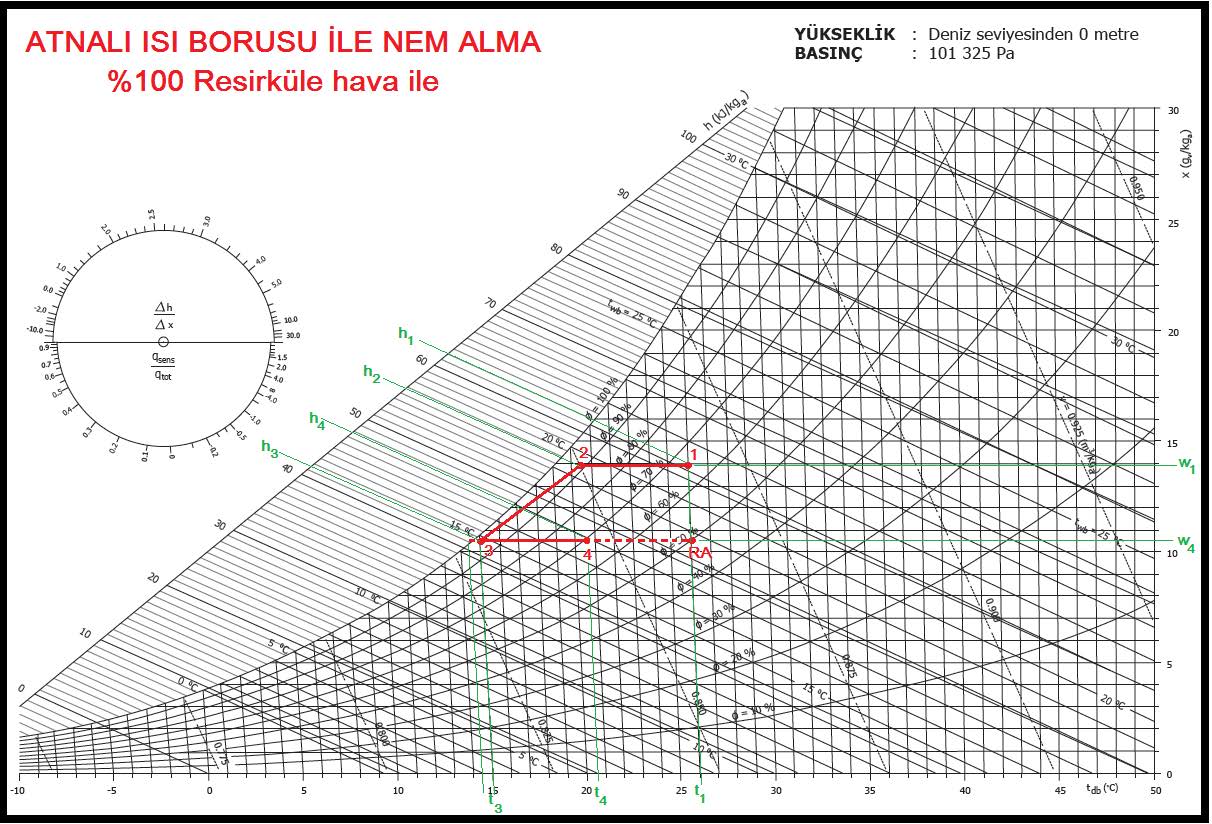
1.4. KARIŞIM HAVALI KLİMA SANTRALI, ISITMA VE HAVA YIKAYICI İLE NEMLENDİRME
Problem: Toplam hacmi 1200 m3olan bir mahallin ısı kaybı 26 kw’tır. Bu mahallin havasının saatte 8 defa değiştirilmesi ve %50 harici hava kullanılması istenmektedir. Dış hava kış dizayn şartları -10oCKT,%70 rH, mahal şartları ise 20oCKT, %50 rH’tır.Klima santralında hava yıkayıcı ile nemlendirme yapılıp, üfleme havasının mutlak neminin oda şartlarına çıkarılması istenmektedir. Klima santralındaki psikrometrik prosesi çizin ve klima santralının tasarımını yapın.
1 kJ = 0.238846 kCal
1 Watt= 0.86 kCal/h
Mahal için gerekli hava debisi ise: V=8 x 1200 = 9600 m3/saat bulunur.
Mahal sıcaklığı 20oC ve hava debisi 9600 m3/saat olduğuna göre, mahal ısı kaybını karşılamak için gerekli üfleme sıcaklığını bulalım.
Qmahal=V x cpx (1/γ)x (tSA – tRA)
cp=Havanın özgül ısısı…………………………………………….. 1.041 kJ/kg
ϒ =Havanın özgül hacmi (ortalama)..………………………. 0.800 m3/kg
Değerleri yerine koyduğumuzda, daha önceki problem çözümlerinde olduğu gibi:
93617= 9600 x 1.041 x( 1/0.800)x(tSA – 20)
tSA = 27.49oC ≈ 28oC bulunur. Bu sıcaklık psikrometrik diyagramda “SA” olarak gösterilmektedir.
%50 dış hava ile %50 dönüş havasının karışım konumu OA-RA proses hattının tam ortasında olup aşağıdaki değerlere sahiptir.
tKa= +5oCKT
hKa= 15.6 kJ/kg
wKa=4.2 gr/kgda
Mahal şartları (RA) :
tRA= +20oCKT
hRA= 38.8.0 kJ/kg
wRA=7.3 gr/kgda (=%50 rH)
Dış hava şartları (OA):
tOA= -10oCKT
hOA= -7.2585 kJ/kg
Daha önceden belirlenen üfleme havası (SA) şartları:
tSA= +28oCKT
hSA= 47.0 kJ/kg
wSA=7.3 gr/kgda
Ön ısıtıcı batarya çıkışı “1” konumunun değerleri:
t1= +18.6oCKT
h1= 29.5 kJ/kg
w1=4.2 gr/kgda
Hava yıkayıcı çıkışı “2” değerleri:
t2= +11.3oCKT
h2= 29.5 kJ/kg
w2=7.3 gr/kgda
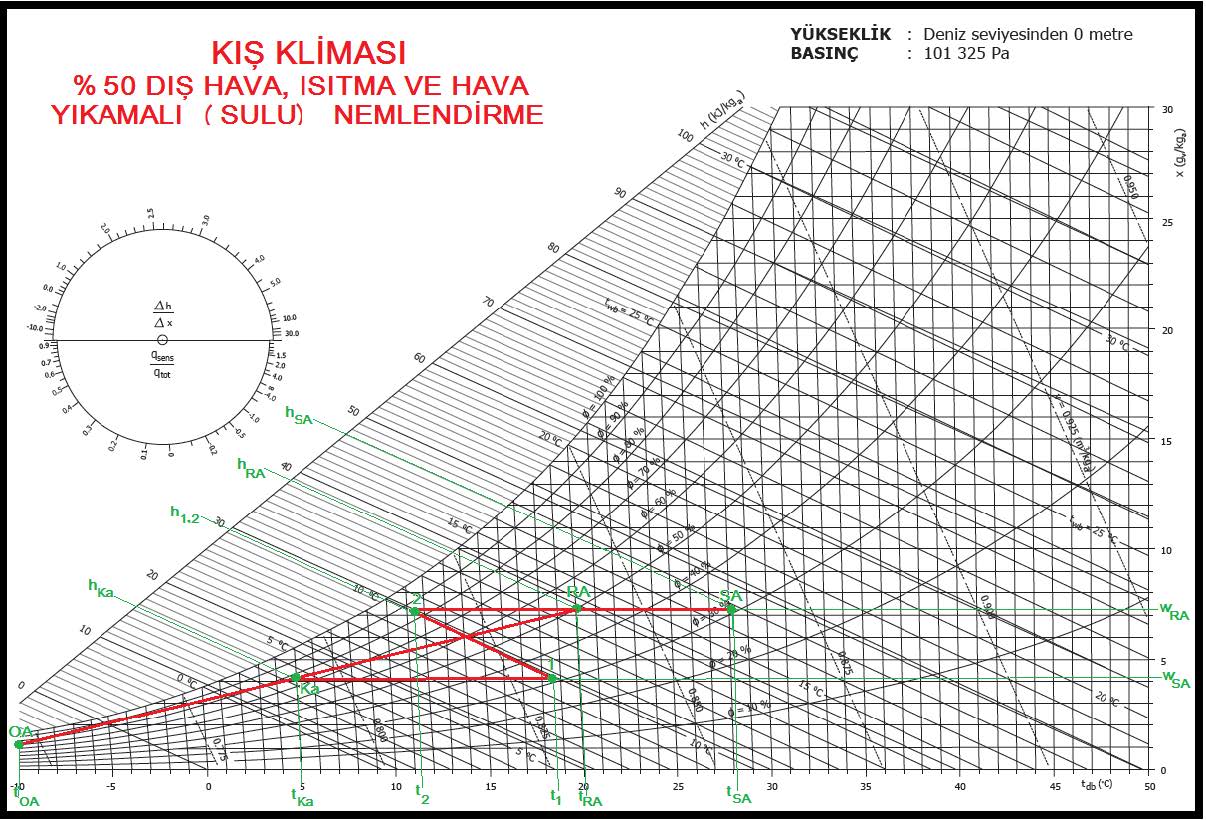
Psikrometrik proses bir önceki, %100 dış havalı sistemin benzeridir. Ön ısıtıcı batarya kapasitesi:
Qön ısıtıcı=V x (1/γ)x (h1– hKA)
Qön ısıtıcı=9600 x (1/0.800)x (29.50+15.60)
Qön ısıtıcı= 166 800 kJ/saat
Qön ısıtıcı = 46.33 kW
Son ısıtıcı kapasitesi:
Qson ısıtıcı=V x (1/γ)x (hSA– h2)
Qson ısıtıcı=9600 x (1/0.800)x (47.00-29.50)
Qson ısıtıcı= 210 000 kJ/saat
Qson ısıtıcı = 58.32 kW
Son ısıtıcı batarya kapasitesinin 26 kW’ı mahal ısı kayıplarını karşılamak, bakiye ise hava yıkayıcıda evaporatif olarak soğuyan havanın mahal kuru termometre sıcaklığına kadar ısıtılması için gerekli olan ısı miktarıdır.
1.5. %100 DIŞ HAVALI KLİMA SANTRALI, ISITMA VE BUHARLI NEMLENDİRİCİ İLE NEMLENDİRME
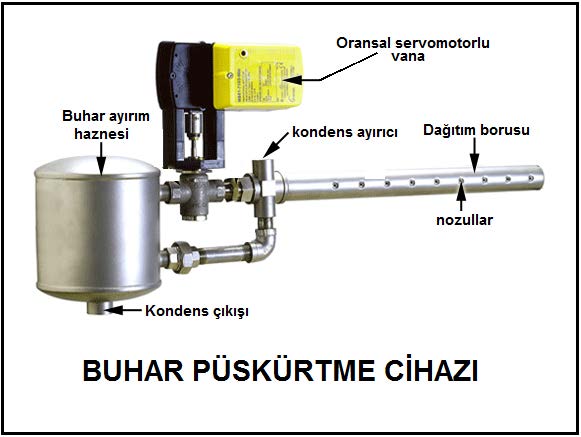
Buharlı nemlendirmenin sağladığı en büyük avantaj klima santralının boyunun kısalması ve daha az yer işgal etmesidir. Buharlı nemlendiricilerin buhar püskürtme probları santral gövdesi içine yerleştirilebileceği gibi üfleme kanalına da yerleştirilebilir.
Buharlı nemlendirmenin diğer bir üstünlüğü de hassas bir oransal kontrol yapabilme olanağıdır. Hava yıkayıcılı nemlendirmede çok zor olan bu uygulama, iki yollu bir oransal vana ve oransal bir higrostat ile (veya DDC/BMS uygulaması varsa bir bağıl nem hissedici ile)kolaylıkla gerçekleştirilebilir.
Atık buharın mevcut olduğu, büyük lokanta, hastane, otel be benzeri tesislerde de son derece ekonomik çözümler getirir.
Burada da, devamlılık açısından, 1.3. numaralı konuda ele aldığımız mahallin kış klimasını bu sefer buharlı nemlendirici ile yapacağız.
Problem: Toplam hacmi 1200 m3olan bir mahallin ısı kaybı 26 kw’tır. Bu mahallin havasının saatte 8 defa değiştirilmesi ve %100 harici hava kullanılması istenmektedir. Dış hava kış dizayn şartları -10oCKT,%70 rH, mahal şartları ise 20oCKT, %50 rH’tır.Klima santralında havanın nemlendirilmesinin buharlı nemlendirici ile yapılıp, üfleme havasının mutlak neminin oda şartlarına çıkarılması istenmektedir. Klima santralındaki psikrometrik prosesi çizin ve klima santralının tasarımını yapın.
1 kJ = 0.238846 kCal
1 Watt= 0.86 kCal/h dolayısıyla
1 Watt= 0.86/0.238846 = 3.60065 kJ ; 1kW= 3600.65kJ
Bu durumda yeni “SI” birimlerine göre mahallin ısı yükü:
26 kW x 3600.65=93617 kJ/saat’tir.
Mahal için gerekli hava debisi ise:
V=8 x 1200 = 9600 m3/saat bulunur.
Mahal sıcaklığı 20oC ve hava debisi 9600 m3/saat olduğuna göre, mahal ısı kaybını karşılamak için gerekli üfleme sıcaklığını bulalım.
Qmahal=V x cpx (1/γ)x (tSA – tRA)
cp=Havanın özgül ısısı…………………………………………….. 1.041 kJ/kg
γ=Havanın özgül hacmi (ortalama)..………………………. 0.800 m3/kg
Değerleri yerine koyduğumuzda, daha önceki problem çözümlerinde olduğu gibi:
93617= 9600 x 1.041 x( 1/0.800)x(tSA – 20)
tSA = 27.49oC ≈ 28oC bulunur. Bu sıcaklık psikrometrik diyagramda “SA” olarak gösterilmektedir. Bu nedenle -10oCKT sıcaklığındaki dış hava +28oCKT sıcaklığına kadar ısıtılacaktır.
Bu duruma göre:
Q=V x (1/γ)x (h1 – hOA)
Q=9600 x (1/0.800)x (31.60+7.2585)
Q= 466 302 kJ/saat
Q= 466 302 /3600.65=129.50 Kw
(hSA= 31.60 kJ/kg …………………… ( psikrometrik diyagramdan))
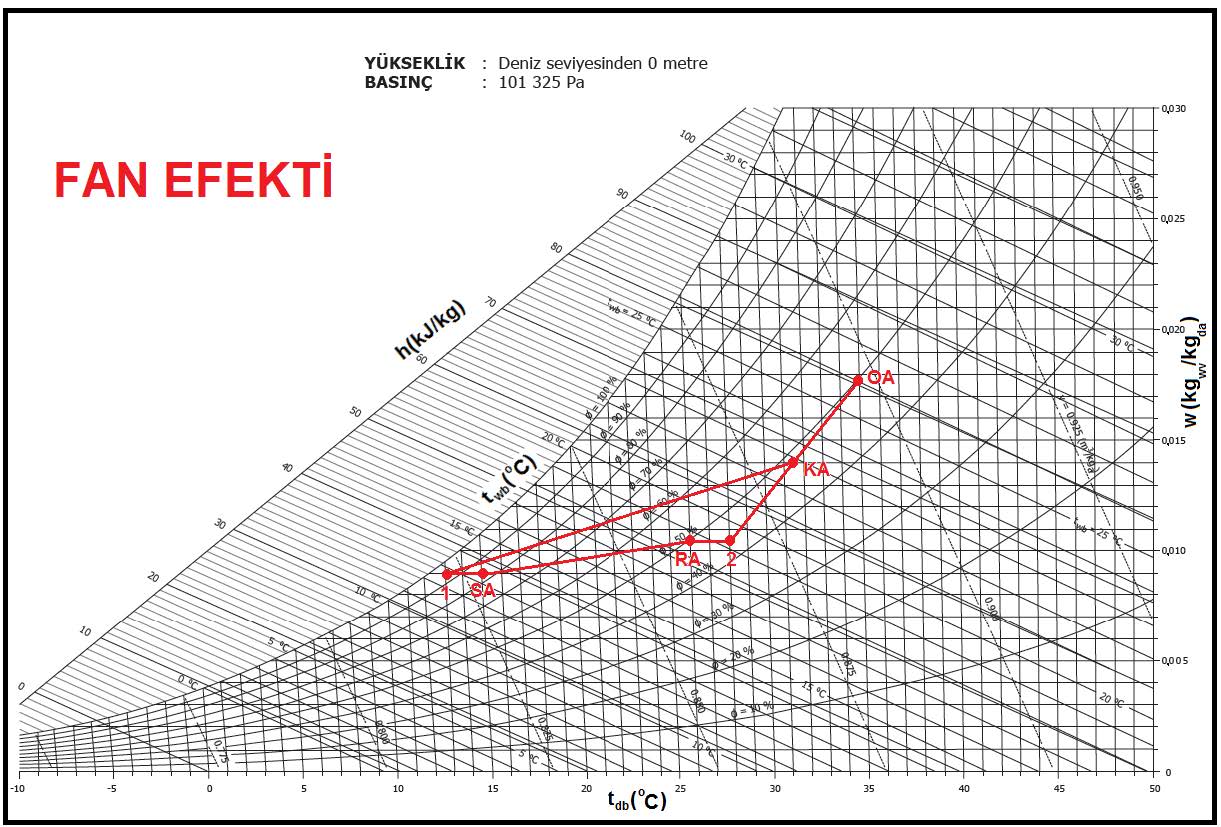
Buhar ile nemlendirme izotermik bir proses olarak tanımlanır. Havaya doğrudan buhar ilave ettiğimiz için yalnız havanın mutlak nem oranı artmakta, sıcaklığın sabit kaldığı kabul edilmektedir. Örneğin buharın sıcaklığı ile buhar üflenen havanın kuru termometre sıcaklıkları birbirine eşit olması durumunda bu varsayım doğrudur. Ancak hakikatte bu proses psikrometrik diyagramda hafif sağa yatan bir doğru tarzında oluşur. Çünkü üflenen buharın sıcaklığı havanın kuru termometre sıcaklığından çok yüksektir. Bu nedenle havayı nemlendirmeye ilaveten az da olsa havayı bir miktar ısıtmış olur.
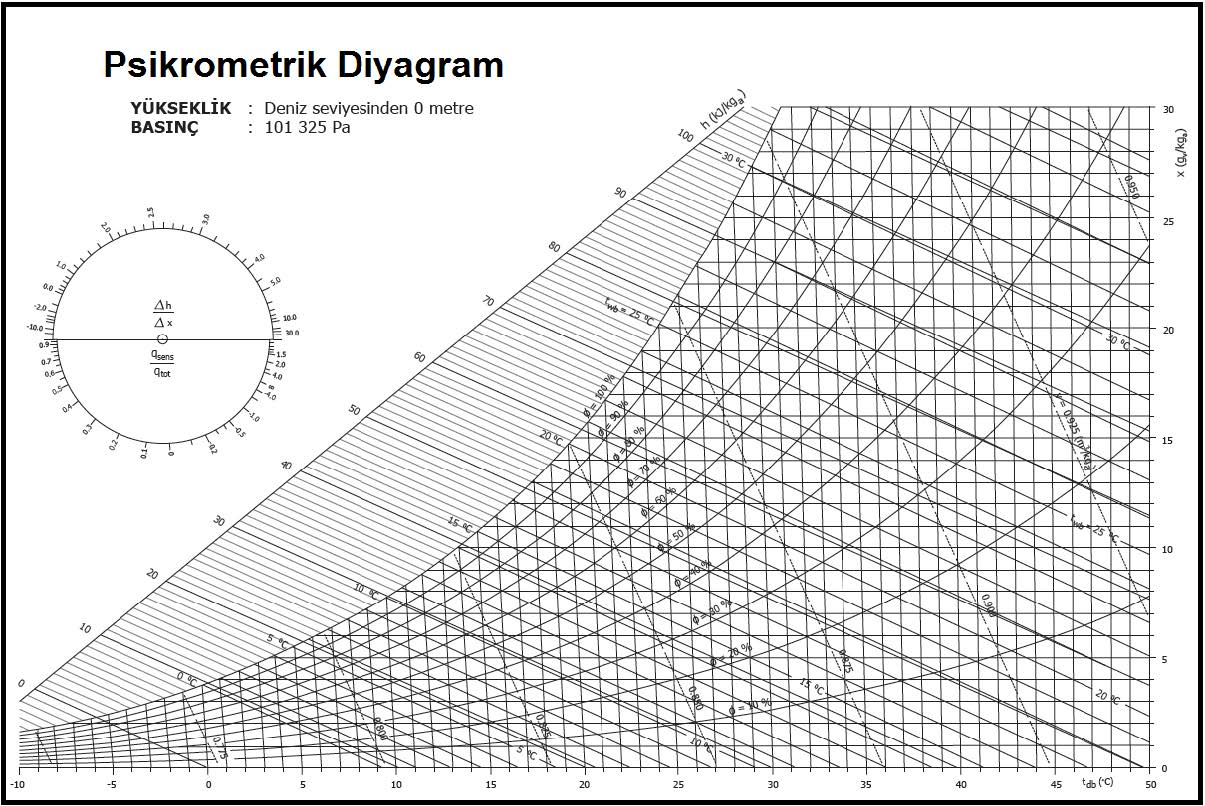
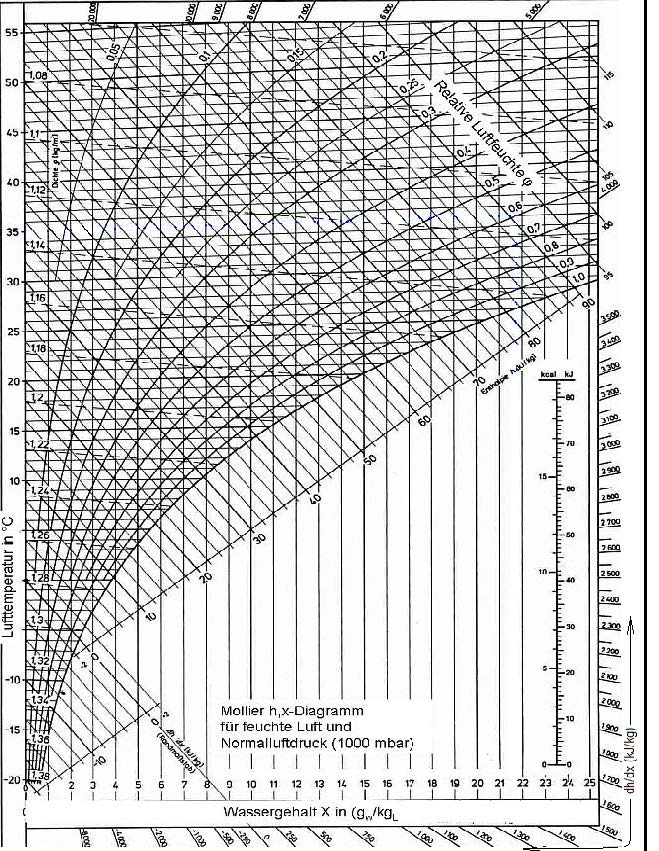
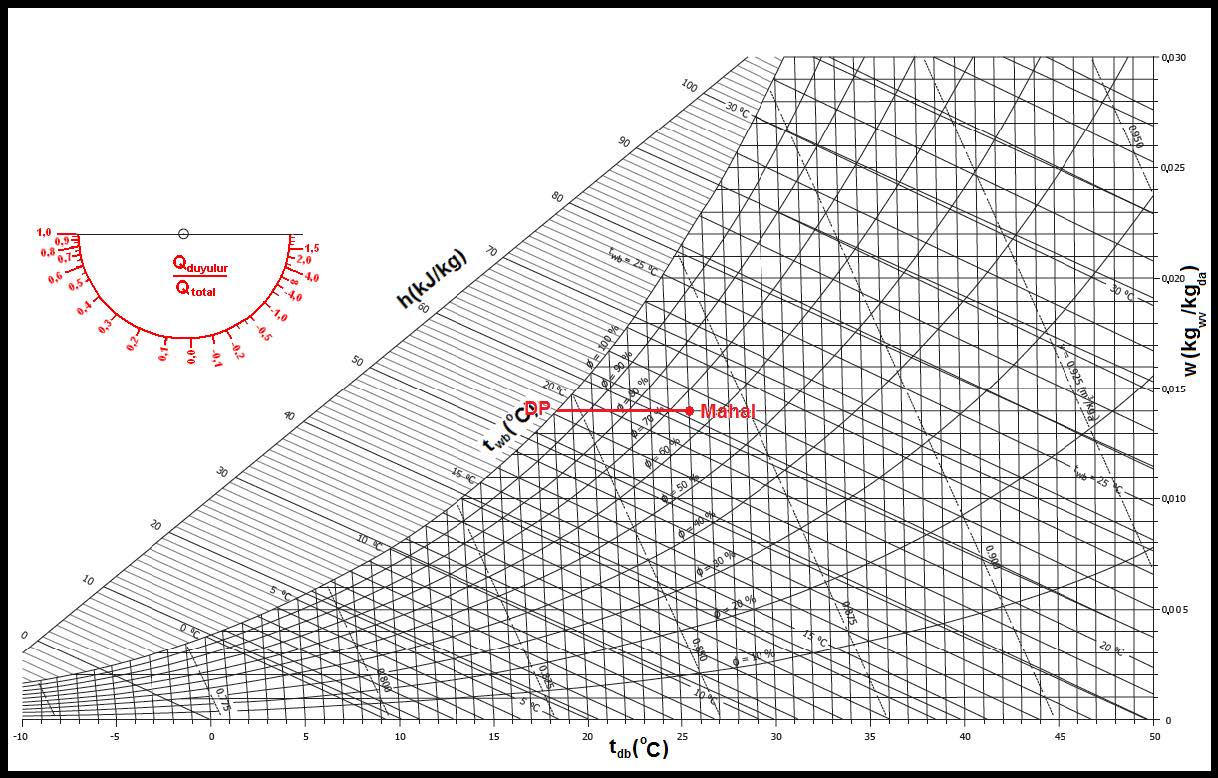
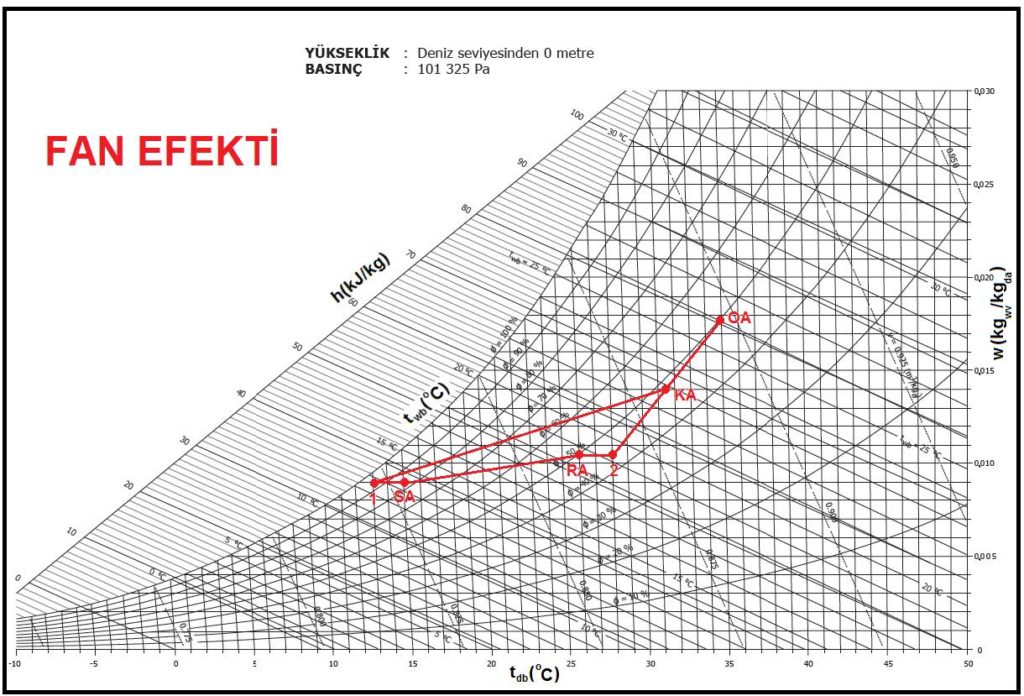
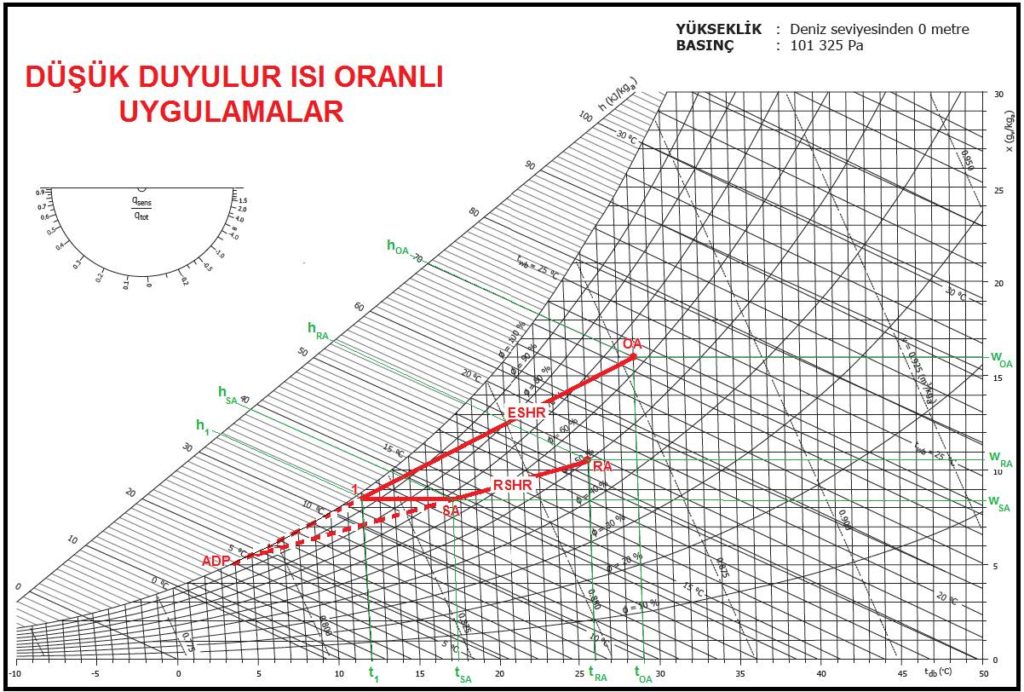
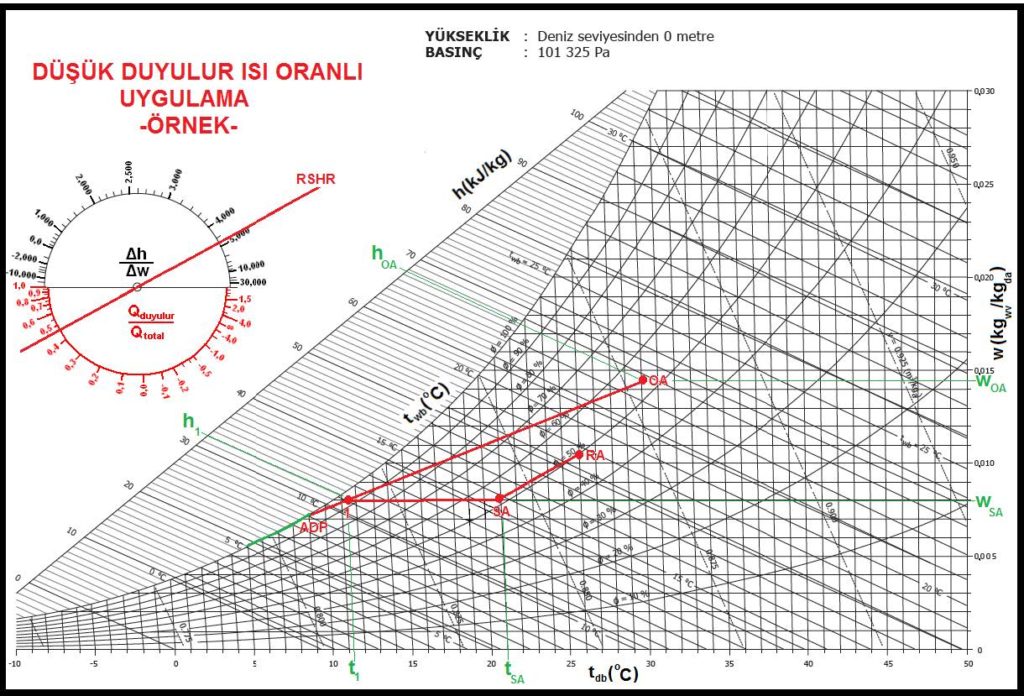
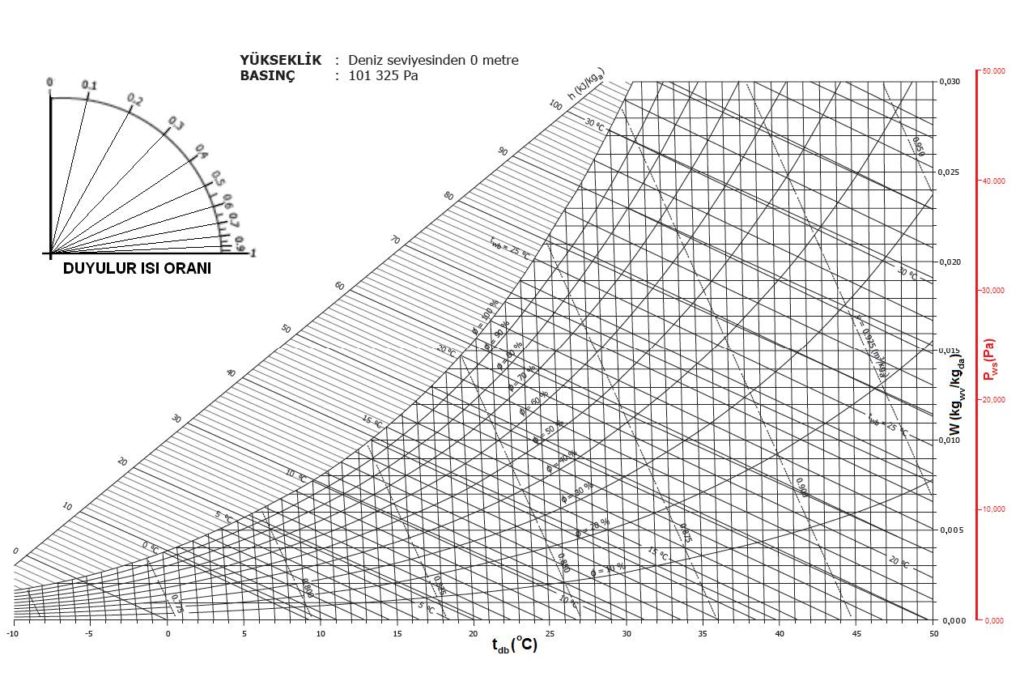
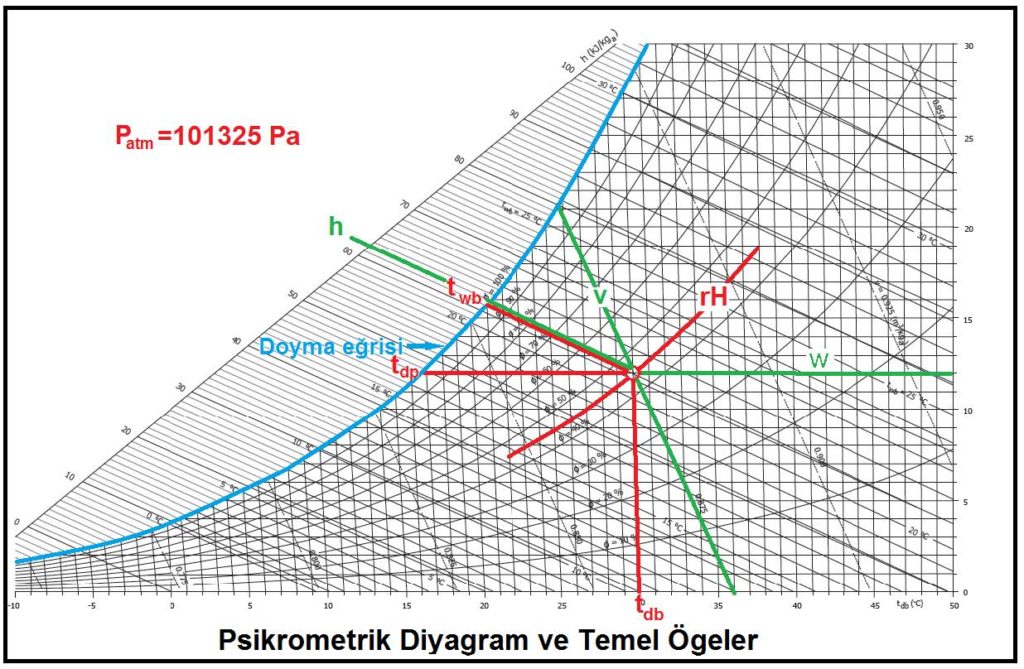
Aşağıdaki psikrometrik diyagramda bu prosesi görmekteyiz. Burada psikrometrik diyagramda bulunan yeni bir şema ile karşılaşıyoruz. Dairesel olan bu şema “Psikrometri-I” kitabımızda deteylı bir biçimde anlatılmıştı. Ancak kısaca tekrarında fayda görüyoruz.
Bu daire ortadan ikiye bölünmüş olup alt kısmı duyulur ısı oranını “qsens/qtot” vermektedir. Üst kısmı ise “Δh/Δw” değeridir. Bu değer bir gram buharın entalpik değerine eşit olup bize buharlı nemlendiricilerde proses hattının eğimini belirler.
Jeneratör tipi buharlı nemlendiricilerde jeneratör buhar çıkış sıcaklığı 102 ila 103oC civarındadır. Ancak boru şebekesi içinde soğuma olabilmesi ihtimali dikkate alınarak buhar üfleme sıcaklığı 100oC kabul edilebilir. 100oC buharın entalpisi “hg-100” 2675.57 kJ/kg’dır (bkz, Psikrometri-I, sayfa-26, Tablo-2).
hg-100= 2675.57 kJ/kg = 2.67557 kJ/gr.
Biz de üst yarı dairede 2.67557 noktasını bulup bu noktası dairenin merkeziyle birleştiririz. Bu bizim nemlendirme proses hattımızın eğimidir. Bu hattı “SA” noktasına taşıyıp, “OA-1” ısıtma proses hattıyla kesiştiriz. “1” noktasının kuru termometre sıcaklığı 28oC değil, aslında 27.3oCKT’dir. Bu değeri dikkate alarak ısıtıcı batarya kapasitesini yenileyebiliriz.
Q=V x (1/γ)x (h2 – hOA)
Q=9600 x (1/0.800)x (30.50+7.2585)
Q= 453 102 kJ/saat
Q= 453 102 /3600.65=125.84 Kw bulunur.
Buharlı nemlendiricinin kapasite de aşağıdaki gibi hesaplanır:
WOA= 1.2 gr/kgda
WRA= 7.4 gr/kgda
ϒ = 0.850 m3/kg (ortalama değer)
Mbuhar= V x (1/γ) x (WRA– WOA)
Mbuhar= 9600 x (1/0.850) x (7.4 – 1.2)
Mbuhar= 70 023.53 gr/saat = 70 kg/saat
Bu sistem için gerekli olan buhar jeneratörünün kapasitesi 70 kg/saat olmalıdır.
Jeneratörün elektrik sarfiyatını hesaplayalım (%100 adyabatik olduğu kabulüyle)
hf-15 = 62.98 kJ/kg ………….(suyun 15oC’ta jeneratöre geldiği varsayımıyla)
hg-103=2680.28 kJ/kg
Q=M x (hg-103– hf-15 )
Q=70 x (2680.28 – 62.98 )
Q=183 211 kJ/saat = 50.88 kW
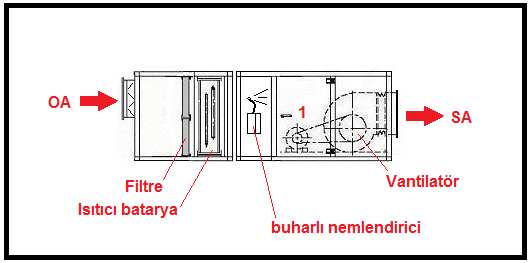
Buharlı nemlendirici bünyesinde olan %100 dış havalı klima santralı şematik olarak aşağıdadır.
 1.6. KARIŞIM HAVALI KLİMA SANTRALI, ISITMA VE BUHARLI NEMLENDİRİCİ İLE NEMLENDİRME
1.6. KARIŞIM HAVALI KLİMA SANTRALI, ISITMA VE BUHARLI NEMLENDİRİCİ İLE NEMLENDİRME
Problem: Toplam hacmi 1200 m3olan bir mahallin ısı kaybı 26 kw’tır. Bu mahallin havasının saatte 8 defa değiştirilmesi ve %30 harici hava kullanılması istenmektedir. Dış hava kış dizayn şartları -10oCKT,%70 rH, mahal şartları ise 20oCKT, %50 rH’tır.Klima santralında havanın nemlendirilmesinin buharlı nemlendirici ile yapılıp, üfleme havasının mutlak neminin oda şartlarına çıkarılması istenmektedir. Klima santralındaki psikrometrik prosesi çizin ve klima santralının tasarımını yapın.
Önceki problemlerde sunduğumuz değişim çarpanlarını, mahal ısı yükünü belirleyelim.
1 kJ = 0.238846 kCal
1 Watt= 0.86 kCal/h dolayısıyla
1 Watt= 0.86/0.238846 = 3.60065 kJ ; 1kW= 3600.65kJ
Bu durumda yeni “SI” birimlerine göre mahallin ısı yükü:
26 kW x 3600.65=93617 kJ/saat’tir.
Mahal için gerekli hava debisi :
V=8 x 1200 = 9600 m3/saat olduğuna göre,
Mahal ısı kaybını karşılamak için gerekli üfleme sıcaklığını bulalım.
Qmahal=V x cpx (1/γ)x (tSA – tRA)
cp=Havanın özgül ısısı…………………………………………….. 1.041 kJ/kg
γ=Havanın özgül hacmi (ortalama)..………………………. 0.800 m3/kg
Değerleri yerine koyduğumuzda, daha önceki problem çözümlerinde olduğu gibi:
93617= 9600 x 1.041 x( 1/0.800)x(tSA – 20)
tSA= 27.49oC ≈ 28oC bulunur. Bu sıcaklık psikrometrik diyagramda “SA” olarak gösterilmektedir.
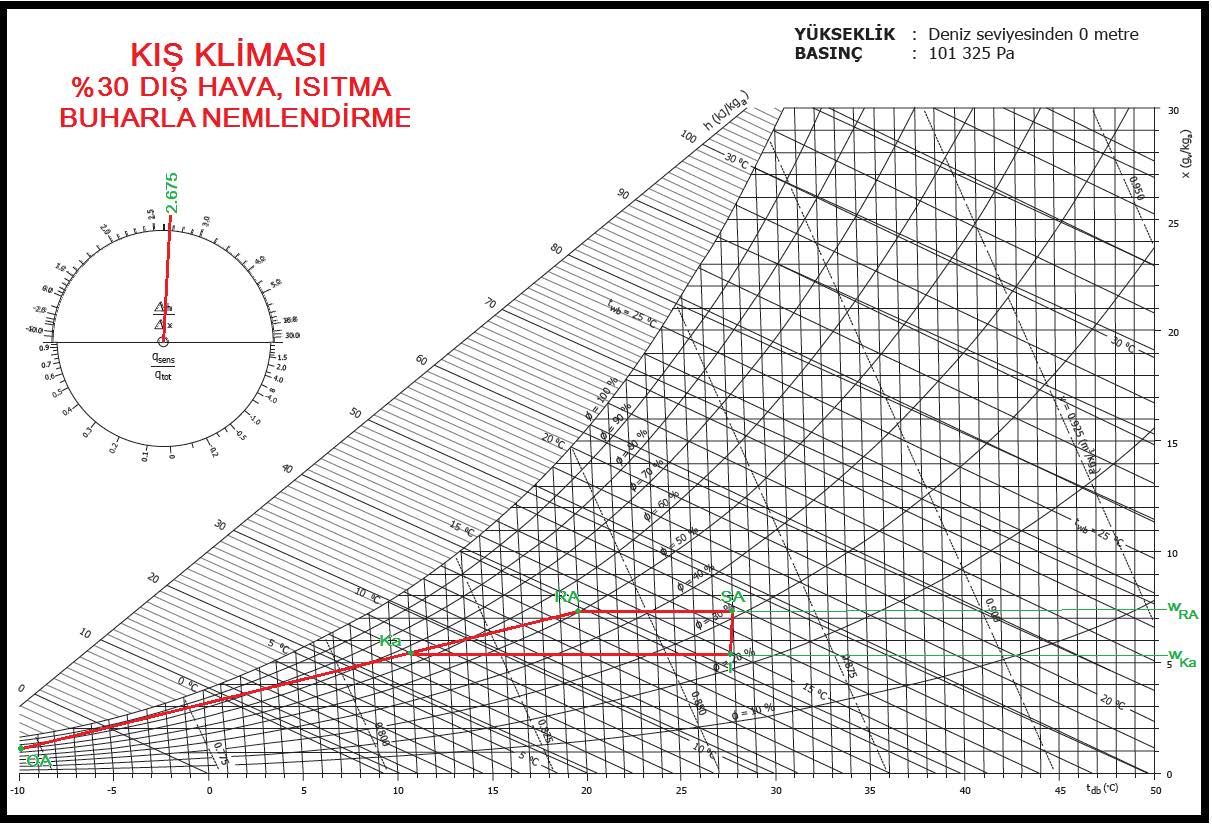
Buradaki çözüm bir önceki, %100 dış havalı çözüme benzemektedir. Ancak bu uygulamada %30 dış hava kullanılmaktadır. Bu nedenle OA-RA proses hattı üzerinde %30 karışım noktası belirlenir. “Ka” olarak adlandırdığımız bu noktadan sabit mutlak nem oranında, yatay bir hat çizilir. Bu bizim ısıtma proses eğrimiz olacaktır.
Diğer yatay bir bir hat ta kesik çizgi halinde “RA” noktasından çizilir. Bu hat üzerindeki 28oCKT noktası bizim klimatize üfleme havası konumu “SA”dır. “Δh/ Δx” çemberi üzerindeki 2.675 değeri ile daire merkezini birleştiren hattı paralel olarak “SA” noktasına taşıyıp uzatır ve “OA”dan gelen yatay hatla kesişmesini sağlarız. Bu bizim “1” konumumuz olup ısıtıcı batarya çıkış şartıdır. 1.6. sayılı konuda anlattığımız gibi buharla nemlendirme hattı tam bir isotermik hat değildir, üflenen buharın sıcaklığına göre belirlenir.
Bu duruma göre:
Q=V x (1/γ)x (h1 – hKa)
(h1= 42.00 kJ/kg …………………… ( psikrometrik diyagramdan))
(hKa= 25.00 kJ/kg …………………… ( psikrometrik diyagramdan))
Q=9600 x (1/0.800)x (42.00+25.00)
Q= 204 000 kJ/saat
Q= 204 000 /3600.65= 56.66 Kw
Buharlı nemlendirici kapasitesi:
WKa= 5.3 gr/kgda
WRA= 7.4 gr/kgda
γ = 0.850 m3/kg (ortalama değer)
Mbuhar= V x (1/γ) x (WRA– WKa)
Mbuhar= 9600 x (1/0.850) x (7.4 – 5.3)
Mbuhar= 23 717.65 gr/saat = 24 kg/saat
Bu sistem için gerekli olan buhar jeneratörünün kapasitesi 24 kg/saat olmalıdır.
Jeneratörün elektrik sarfiyatını hesaplayalım (%100 adyabatik olduğu kabulüyle)
hf-15 = 62.98 kJ/kg ………….(suyun 15oC’ta jeneratöre geldiği varsayımıyla)
hg-103=2680.28 kJ/kg
Q=M x (hg-103– hf-15 )
Q=24 x (2680.28 – 62.98 )
Q=62 815 kJ/saat = 17.45 kW bulunur.
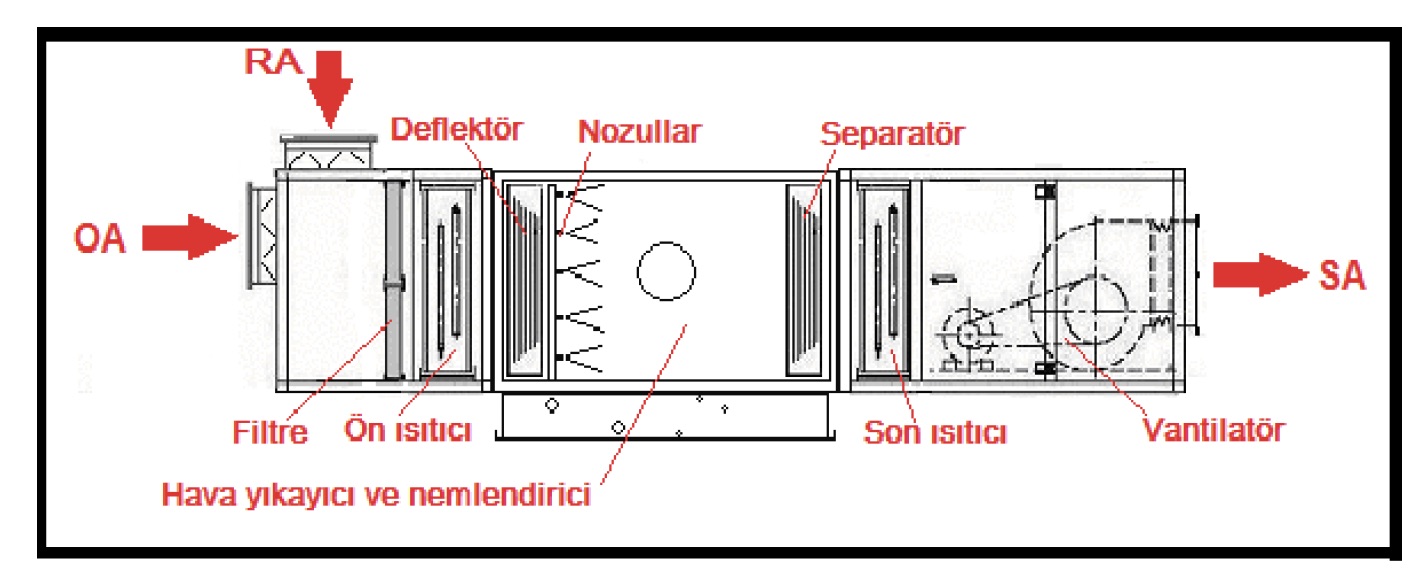
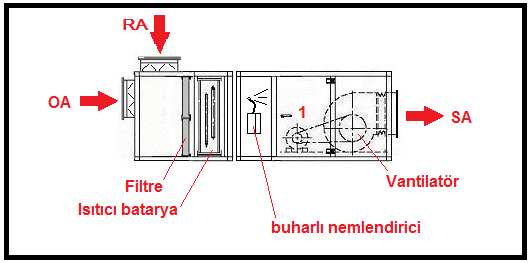
Karışım havalı, buharlı nemlendiricili, yalnız ısıtma bataryalı klima santralının çizimi aşağıda görülmektedir.
 1.7. DÖNÜŞ KANALINDAKİ SOĞUMANIN İNCELENMESİ
1.7. DÖNÜŞ KANALINDAKİ SOĞUMANIN İNCELENMESİ
Şu ana kadar yaptığımız tüm uygulamalarda dönüş havası kuru termometre sıcaklığını oda sıcaklığına eşit olarak kabul ettik. Ancak hakikatte bu durum biraz farklıdır. Eğer dönüş havası kanalları ısıtılmamış (klimatize edilmemiş) mahallerden geçiyorsa kış uygulamasında belirli bir oranda ısı kaybına uğrayacak, bunun neticesi olarak ta dönüş havası kuru termometre sıcaklığında belirgin bir düşme olacaktır. Eğer dönüş havası kanalları izole edilmemişse bu sıcaklık düşüşü çok daha belirgin ve daha büyük değerlerde olacaktır. Bu husus ısıtıcı batarya büyüklüğü belirlenirken dikkate alınması gereken bir husustur.
Dönüş havasındaki soğumayı hesap yoluyla bulmak mümkündür. Bunun için öncelikle ısıtılmamış mahallerin sıcaklıklarının bilinmesi veya hesaplanması gerekir. Hesaplanması gereken ikinci bir husus ta dönüş havası kanalının toplam satıh alanıdır. Kanal ısı iletim katsayısı bilindiğine veya kolaylıkla hesaplanabileceğine göre ısı kaybı ve bunun neticesi dönüş havasındaki soğuma hesap yoluyla bulunabilir. Ancak bu hesap yöntemi ile elde edilecek sonuç yaklaşık bir değer olacağından soğuma kabul edilebilir. Soğuma ve sıcaklık düşümü dış hava sıcaklığına da son derece bağlıdır. Ancak bu düşüm izoleli kanallarda sıcaklık düşümü 1oC ila 2oC, izolesiz kanallarda da 2oC ila 4oC kabul edilebilir.
%100 dış hava ile çalışan, ısı geri kazanımsız sistemlerde bu soğumanın hiçbir önemi yoktur. Çünkü havanın tamamı egzost edilmektedir.Ancak düşük dış hava oranıyla çalışan, örneğin %50’nin altında dış hava oranına sahip uygulamalarda karşımıza küçümsenmeyecek değerler çıkar. Bu durumu psikrometrik diyagramda inceleyelim. Önceki örneklerde olduğu gibi -10oCKT, %70 rH dış hava, 20oCKT, %50 rH mahal şartlarında, %20 dış hava oranıyla çalışan bir klima santralını ele alalım. Dönüş havası kanallarının izolesiz olması nedeniyle dönüş havasında 3oC soğuma olduğunu, daha önceki örneklerimizde olduğu gibi üfleme havası sıcaklığının da 28oCKT olduğunu kabul edelim. Hava debimiz 9600 m3/saat’tir.
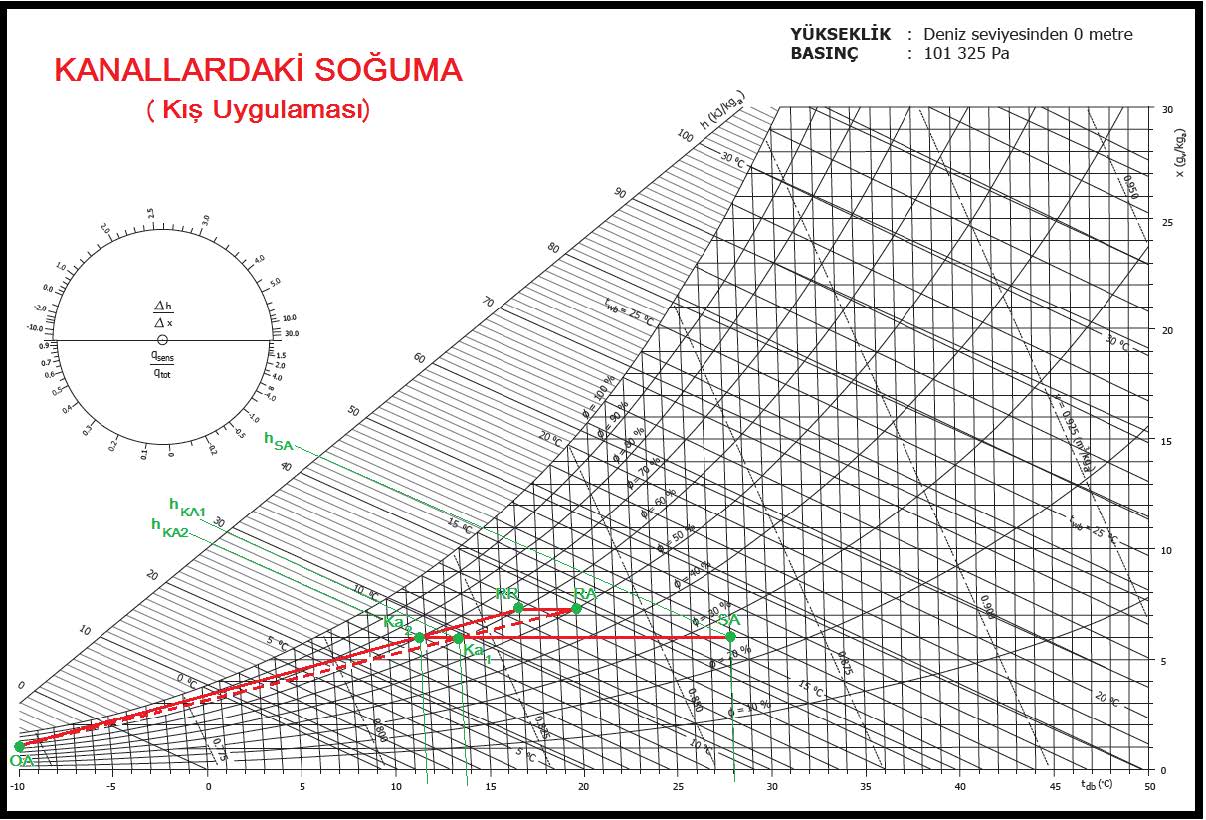
Yukarıdaki psikrometrik diyagramda “RA” mahal şartlarını, “RR” dönüş havasının klima santralına giriş şartlarını, “RA-RR” proses hattı da dönüş kanalındaki soğumayı göstermektedir. Bu soğumanın neticesi karışım noktası “Ka2” olarak belirlenmektedir. Halbuki dönüş hava kanalında hiç ısı kaybı olamasaydı karışım noktası “Ka1” olacaktı. Bu nedenle klima santralı ısıtıcı batarya büyüklüğü belirlenirken “Ka2-Ka1” hattı kadar ilave ısıya ihtiyaç duyulacaktır.
Her iki durum için klima santralı ısıtıcı batarya büyüklüğünü belirleyelim.
Q1=V x (1/γ)x (hSA – hKa1)
Q2=V x (1/γ)x (hSA – hKa2)
Bu denklemlerde:
Q1: Dönüş hava kanalında soğuma olmaksızın ısıtma yükü
Q2: Dönüş hava kanalındaki soğuma dikkate alınarak ısıtma yükü
hKa1= 29.00 kJ/kg
hKa2= 27.00 kJ/kg
hSA = 43.00 kJ/kg
γ = 0.825 m3/kg
Q1=V x (1/ϒ)x (hSA – hKa1)
Q1=9600 x (1/0.825)x (43.00– 29.00)
Q1=162 909 kJ/saat =45.25 Kw
Q2=V x (1/γ)x (hSA – hKa2)
Q2=9600 x (1/0.825)x (43.00– 27.00)
Q2=186 182 kJ/saat = 51.71 kW
Kanaldaki soğuma neticesi 51.71-45.25=6.46 kW daha fazla ısıtmaya ihtiyaç bulunmaktadır.
1.8. ISI GERİ KAZANIM ELEMANLARININ TANIMI
Isı geri kazanım sistemleri “Psikrometri-I” isimli kitabımızda detaylı bir şekilde incelenmişti. Ancak burada kısa bir tanımının yapılmasının faydalı olacağı düşüncesiyle konuyu özet olarak tekrarlıyoruz. Reküperatör, veya Türkçe tabiriyle ısı değiştirgeçlerinin kullanıldığı ısı geri kazanım işlemlerini dört ana grupta toplayabiliriz.
- Çift serpantinli ısı geri kazanım sistemleri
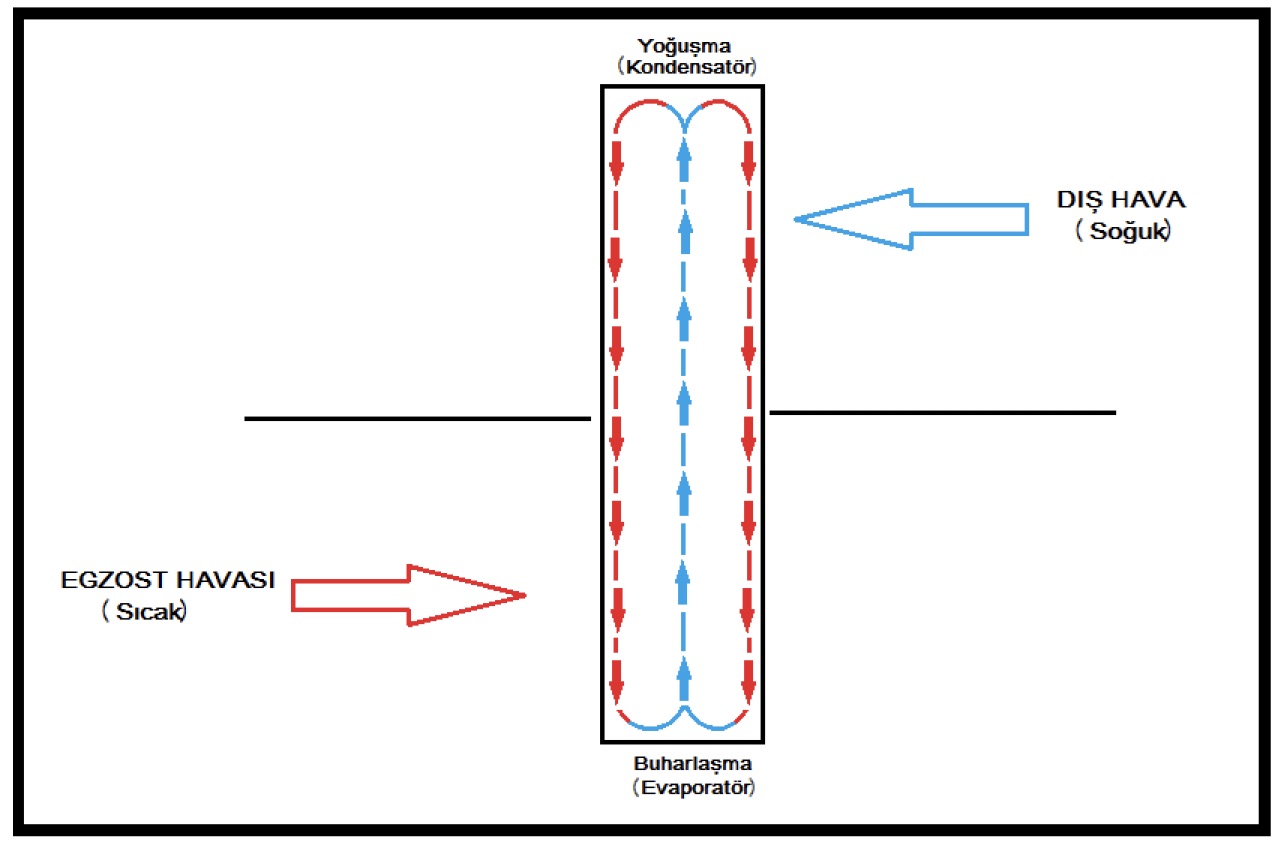
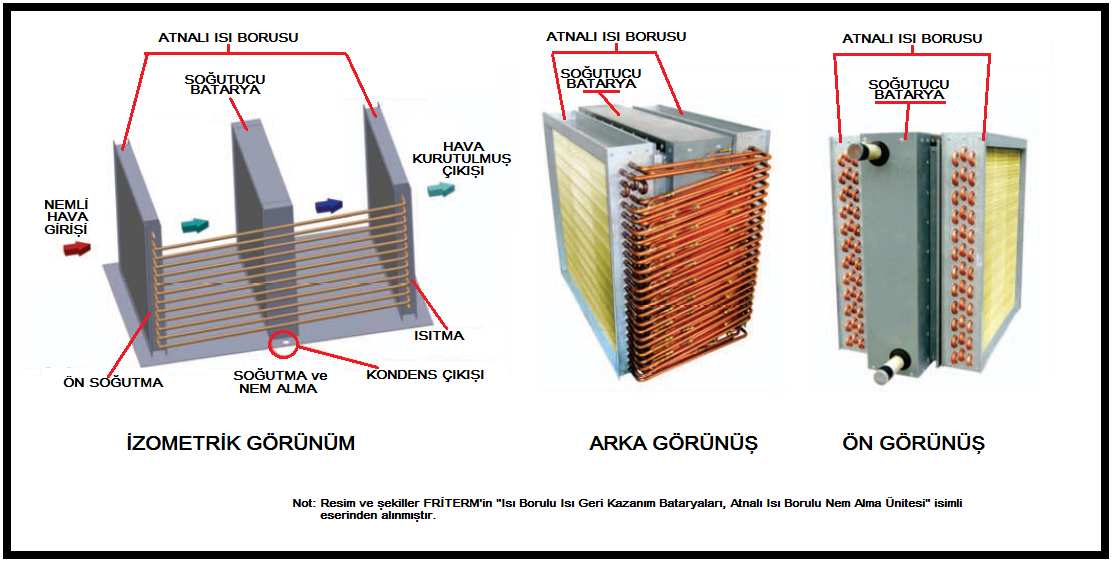
- Isı borulu ısı geri kazanım sistemleri
- Plakalı eşanjörlü ısı geri kazanım sistemleri
- Döner tamburlu ısı geri kazanım sistemleri
Klima santrallarının tasarımı açısından her dört uygulama birbirinden farklılık gösterse de psikrometrik açıdan birbirinin aynıdır. Temel farklılık ısı geri kazanım ünitelerinin ısı geri kazanımı gerçekleştirmede gösterdikleri farklılıktır. Bu açıdan ısı geri kazanım elemanlarını iki ana kategoride toplayabiliriz.
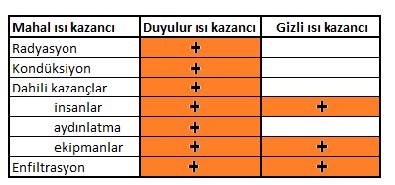
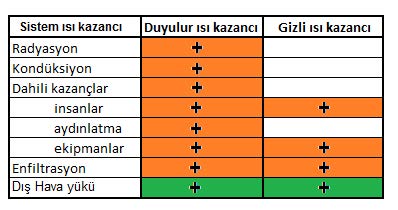
- Yalnız duyulur ısı bazında ısı geri kazanımı gerçekleştirenler
- Entalpi bazında (toplam enerji) bazında ısı geri kazanımı gerçekleştirenler
Diğer bir sınıflandırma da ısı transfer tarzına göredir.
- Direkt ısı transferi ile geri kazanım sağlayanlar
- Üçüncü bir transfer elemanı(hidronik) kullananlar.
Çift serpantinli ısı geri kazanım sistemleri ile ısı borusu geri kazanım sistemleri ısı transferi için hidronik eleman kullanırlar. Bu eleman çift serpantinli sistemlerde su veya su-etilen glikol karışımıdır. Verimi düşük olan (%40 civarı) ve salt duyulur ısı bazında ısı geri kazanımı sağlayan bu sistemin en büyük avantajı vantilasyon ve aspirasyon ünitelerinin aynı mahalde bulunmaları mecburiyetinin olmamasıdır. Örneğin egzost ünitesi çatıda, klima santralı ise bodrum katta olabilir. Transfer boru donanımı ve sirkülasyon pompası vasıtasıyla gerçekleştirilir.
Isı borusunda ise direkt genleşmeye müsait soğutucu akışkandır; en geniş kullanımı olan R-134’dür. Pomapaya gerek göstermeyen, soğutucu akışkanın dansitesinde buharlaşmaya bağlı olarak meydana gelen değişiklikler nedeni sirkülasyonu kendi içinde sağlar. Verim olarak çift serpantinli sistemlere benzerlik gösterirler.
Plakalı eşanjörlerde metal veya LiBr solüsyonu emdirilmiş selülozik elemanlar egzozt ve dış hava arasındaki bölmeyi oluşturur, bu bölme üzerinden ısı iletimi sağlanır. Bu nedenle plakalı ısı geri kazanım eşanjörleri kararlı rejim çalışması olarak kabul edilirler. Plakaları aluminyum veya benzeri metallerden oluşan eşanjörler salt duyulur ısı transferi yapar ve (oC) bazında ısı geri kazanımı sağlar. Selüloz, örneğin LiBr veya benzeri sıvı emdirilmiş kağıt elemanları olanlar duyulur ve gizli ısı transferi yaparlar. Bu eşanjörlere entalpi bazlı ısı geri kazanım eşanjörleri tabir edilir. Plakalı eşanjörlerin verimleri tasarımına bağlı olarak %40 ila %85 arası değişmektedir. Bir plakalı eşanjör aşağıda görülmektedir.
Döner tamburlu eşanjörler salt metal veya satıh kaplamalı metal dolgu malzemesine sahiptirler. Bulundukları klima santralları içinde 80 ila 100 d/dak hızla dönerler. Dönme işlemi küçük bir elektrik motoru vasıtasıyla gerçekleştirilir. Egzost havası tarafındaki tekerleğin yarısı egzost havasının sıcaklığı nedeniyle ısınır ve dönme hareketi neticesi bu havayı soğuk olan dış havaya taşır (yaz aylarında bu işlemin tersi olur). Bu nedenle döner tamburlu ısı geri kazanım eşanjörlerinin çalışma tarzı kararsız rejim olarak kabul edilir. Döner tamburlu eşanjörler üç değişik şekilde imal edilmektedirler:
- Salt metal (aluminyum) dolgu malzemeli olanlar : Bu modeller yalnız duyulur ısı tarnsferinde kullanılırlar. Dönme işlemi neticesi cüzi bir miktar nemli havayı da sürükleseler gizli ısı transferi açısından bu husus kabili ihmaldir. Oldukça yüksek duyulur ısı geri kazancı verimine sahiptirler ((%70 ve üzeri).
- Satıhları oksitlenmiş aluminyum dolgu malzemeli olanlar:Bu modellere antalpi tekerleği de tabir edilir. Aluminyum dolgu malzemeleri özel banyolarda oksitlendirilip belirli bir mikron kalınlığında oksit tabakasına sahip olurlar. Bu eşanjörlerin yüksek duyulur ısı geri kazanım verimlerine (%70 ve üzeri) karşılık gizli ısı geri kazanım verimleri oldukça düşüktür (%40 civarı).
- Dolgu malzemesinin satıhları silika jel kaplı olanlar:Bu modellere absorbsiyon tekerleği de denir. Aluminyum dolgu malzemelerinin sathı özel işlemlerle pulverize silika jel ile kaplanmıştır. Yüksek duyulur ve gizli ısı geri kazanım verimlerine sahiptirler (%70 ve üzeri).
Bu konu ile ilgili detaylı bilgi “Psikrometri-I” kitabında bulunabilir.
1.9. %100 DIŞ HAVALI, DUYULUR ISI GERİ KAZANIMLI, YALNIZ ISITMALI KLİMA SANTRALI.
Problem: Toplam hacmi 1200 m3olan bir mahallin ısı kaybı 26 kw’tır. Bu mahallin havasının saatte 8 defa değiştirilmesi ve %100 harici hava kullanılması istenmektedir. Dış hava kış dizayn şartları -3oCKT, %70 rH, mahal şartları ise 20oCKT, %40 rH’tır. Klima santralında duyulur ısı bazında %55 verimli plakalı ısı geri kazanım eşanjörü kullanılacaktır. Psikrometrik prosesi çizin ve klima santralının tasarımını yapın.
1kW= 3600.65kJ
Bu durumda yeni “SI” birimlerine göre mahallin ısı yükü:
26×3600.65=93617 kJ/saat’tir.
Klima santralının hava debisi : V=1200 m3x 8 defa/saat=9600 m3/saat’tir.
Mahal ısı kaybını karşılamak için gerekli olan üfleme sıcalığı da, daha önceki örneklerimizde olduğu gibi:
Qmahal=V x cpx (1/γ)x (tSA – tRA)
cp=Havanın özgül ısısı…………………………………………….. 1.041 kJ/kg
γ=Havanın özgül hacmi (ortalama)..………………………. 0.800 m3/kg
Değerleri yerine koyduğumuzda:
93617= 9600 x 1.041 x( 1/0.800)x(tSA – 20)
tSA = 27.49oC ≈ 28oC bulunur.
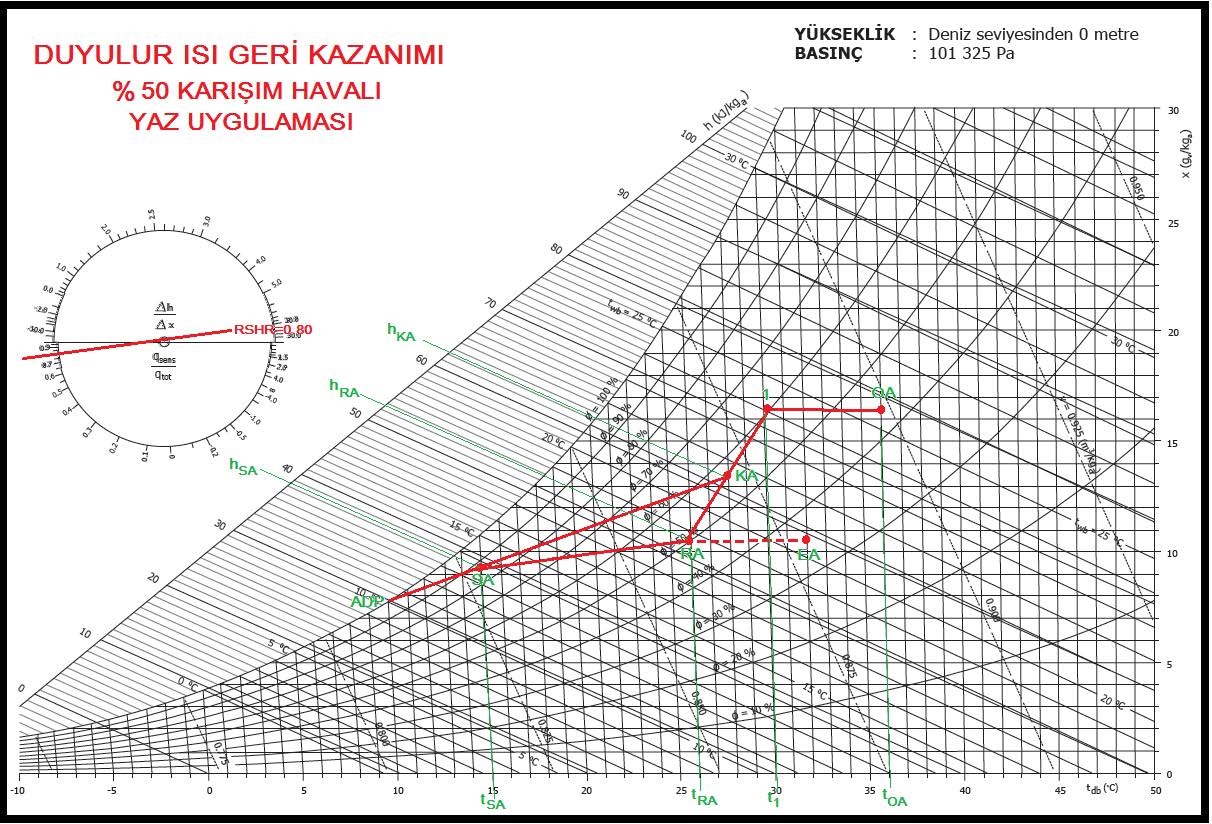
Bu işlemle ilgili prosesler alttaki psikrometrik diyagramda görülmektedir.
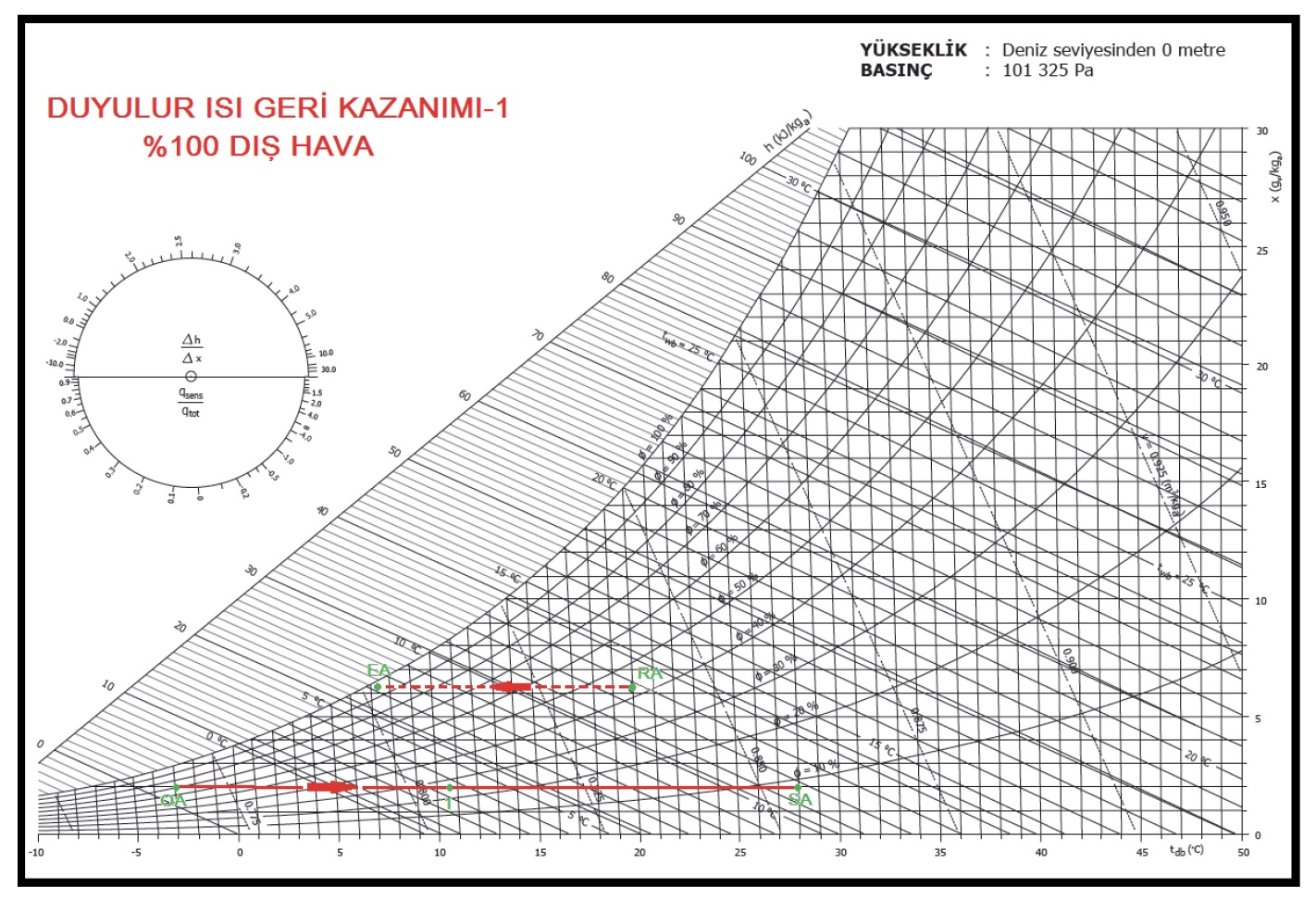
Eğer plakalı ısı geri kazanım eşanjörü kullanılmasaydı “OA” şartlarındaki dış havanın “SA” şartlarına kadar ısıtılması gerekecekti. Bunun için de gerekli olan ısı miktarı:
ΣQ=V x cpx (1/γ)x (tSA– tOA)
ΣQ= 9600 x 1.041 x (1/0.800)x(28+3)
ΣQ= 387 252 kJ/saat = 107.55 kW olacaktı.
Ancak %55 ısı geri kazanım verimli plakalı eşanjör kullanıldığına göre egzost edilen mahal havasının ısısı büyük oranda dış havaya transfer olunacak ve bu sayede önemli miktarda enerji tasarrufu yapılmış olacaktır. Duyulur ısı bazında ısı geri kazanım işleminde dış hava ile mahal havasının mutlak nem oranları eşanjördeki proses nedeniyle değişmemekte, aynı kalmaktadır. Isı alışverişi yalnız duyulur ısı bazında olmaktadır. Isı alışverişi sonucu oluşan sıcaklıkların nasıl nesaplanacağı TS EN-308’de belirtilmiştir.
η=100 x (tRA-tEA)/(tRA-tOA)
Bu formülde:
η= Eşanjörün ısı kazanım verimi……………………………………………………. (%)
tRA= Egzost edilen havanın eşanjöre giriş sıcaklığı …………………………..(oC)
tEA= Egzost edilen havanın eşanjörden çıkış sıcaklığı ……………………….(oC)
tOA= Dış hava sıcaklığı……………………………………………………………………….(oC)
Bizim örneğimizde ısı geri kazanım eşanjörünün verimi %55 olduğuna göre
η=(tRA-tEA)/(tRA-tOA) = 0.55 =(20-tEA)/(20+3)
tEA=7.35oC
Isı geri kazanım işlemi esnasındaki egzost ve dış havaların ortalama yoğunluklarının eşit olduğunu kabul edersek:
η=(t1-tOA)/(tRA-tOA) = 0.60 =(t1+3)/(20+3)
t1= 9.65oC bulunur.
Dolayısıyla egzost edilen mahal havasının duyulur ısısının %60 oranında dış havaya transferi ile önemli bir miktarda ısı tasarrufu sağlanmış bulunmaktadır. Çünkü artık dış hava -3oC’tan +28oC’a değil, +9.65oC’tan +28oC’a ısıtılmış olacaktır. Bu nedenle klima santralındaki ısıtıcı batarya büyüklüğü:
ΣQ=V x cpx (1/γ)x (tSA– t1)
ΣQ= 9600 x 1.041 x (1/0.800)x(28-9.65)
ΣQ= 229 228 kJ/saat = 63.70 kW olacaktır.
Bu uygulama sayesinde:
107.55 – 63.70 = 43.85 kW enerji tasarrufu sağlanmaktadır.
Bu uygulamayla ilgili klima santralı da aşağıdaki şematik resimdedir. Resmimizde plakalı eşanjör kullanılmıştır.
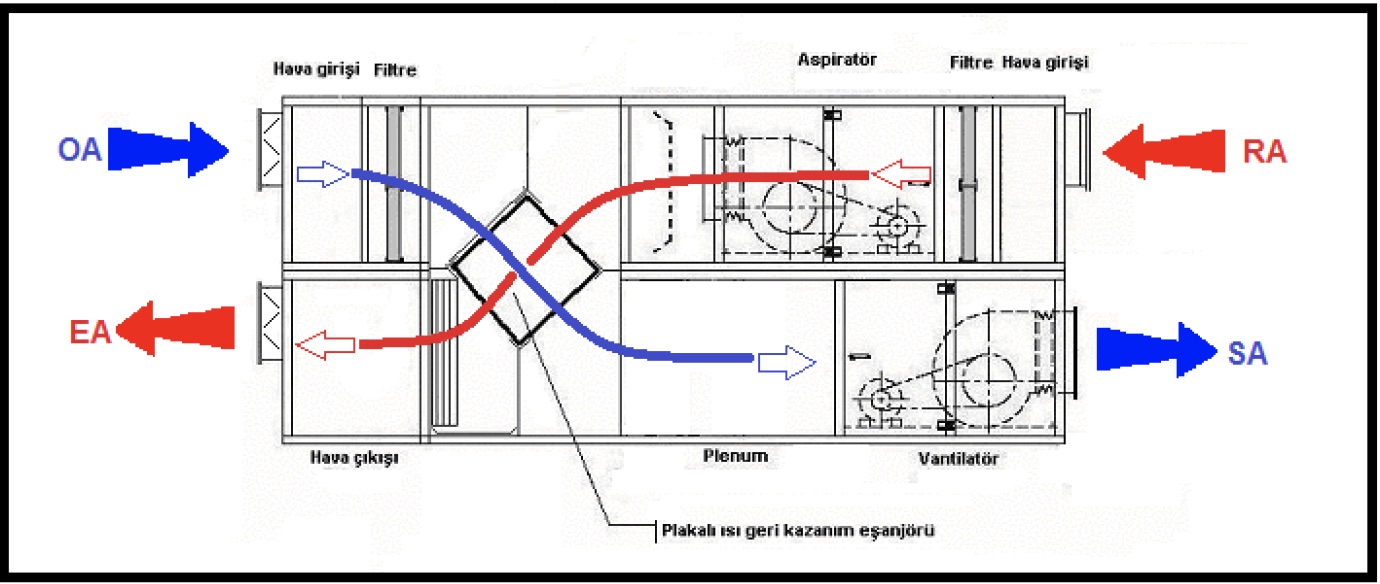
Plakalı eşanjör, döner tambur veya ısı borusu uygulamalarında vantilatör ve aspiratörün aynı klima santralının kabini içinde olması gerekmektedir. Örneğin çizimimizde görüldüğü gibi iki katlı klima santralı uygulaması yapılmalıdır.
Örneğimizde egzost havasında herhangi bir yoğuşma olmamaktadır. Çünkü RA-EA soğuma proses hattı %100 doyma eğrisini kesmemektedir. Soğuma yalnız duyulur soğuma olduğundan herhangi bir soğuma sözkonusu değildir. Bir sonraki örneğimizde yoğuşmalı bir uygulamayı inceleyeceğiz.
Problem: 20oCKT, %50 rH şartlarındaki mahal havası egzost edilmektedir. Egzost edilen miktar 10 000 m3/saat’tir. Aynı miktardaki dış hava da duyulur ısı verimi %60 olan plakalı eşanjörden geçirilerek mahalle sevk edilmektedir. Dış hava şartları -10oCKT, %70rH’tır.
- Mahal havasının eşanjör çıkış sıcaklığını ve yoğuşma miktarını belirleyiniz.
- Dış havanın eşanjörden çıkış sıcaklığını belirleyiniz.
- Transfer edilen ısı miktarını hesaplayınız.
- Eşanjörde karlanma riski var mıdır, irdeleyiniz.
η=100 x (tRA-tEA)/(tRA-tOA)=%60
η=100 x (t1-tOA)/(tRA-tOA)=%60………….. (özgül hacimlerin değişmeyeceği varsayımıyla)
tRA= 20 oC
tOA= -10 oC
Değerleri yerlerine koyduğumuzda:
0.60 = (tRA-tEA)/(tRA-tOA)
0.60 = (20 – tEA)/(20 + 10)
tEA= +2oC
Bu işlemi psikrometrik diyagrama işlediğimizde “EA” konumunun %100 doyma eğrisinin dışında olduğunu görürüz. Bu mümkün değildir (Bkz. Psikrometri-I ). Çünkü 20oCKT, %50 rH
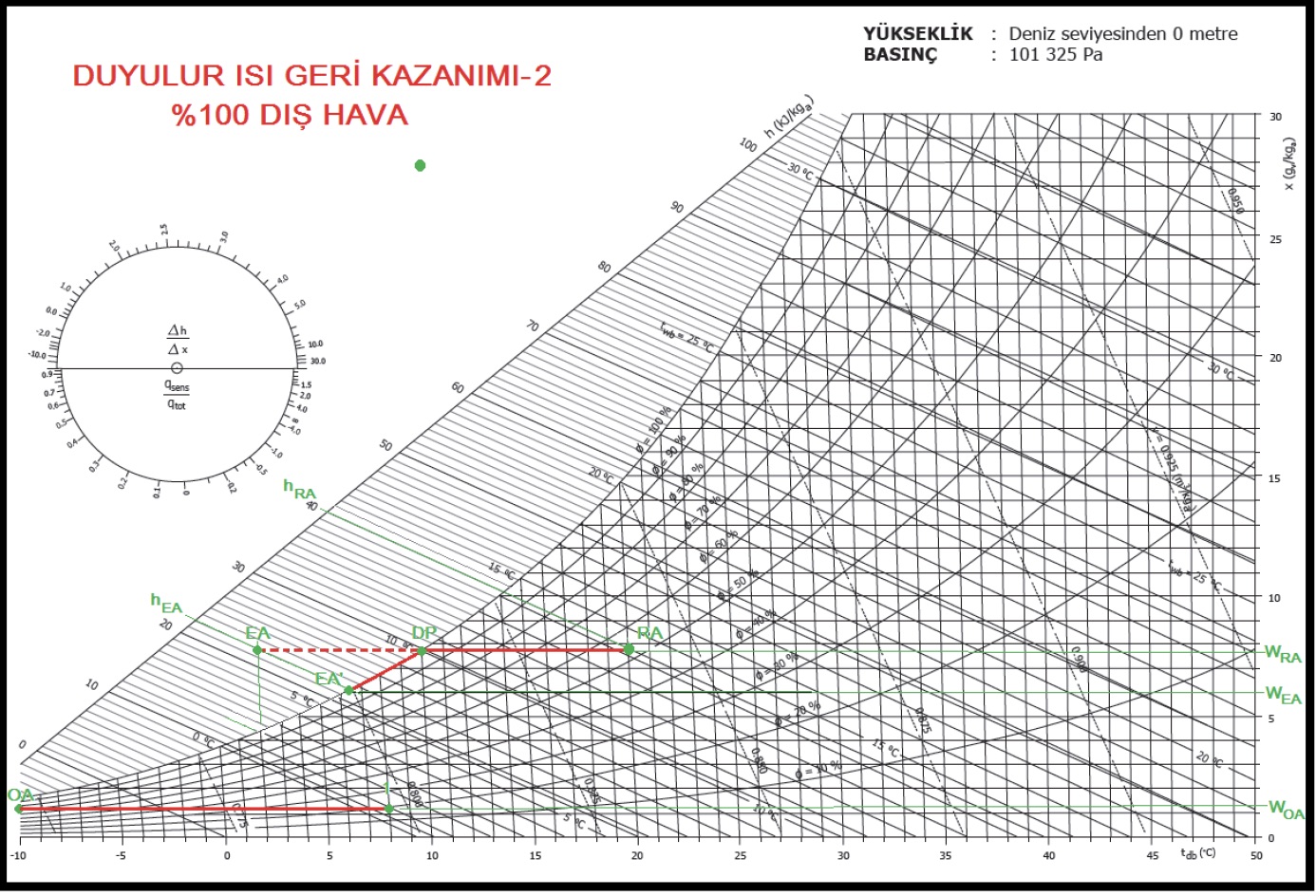
değerlerine sahip “RA” oda konumunun çiy noktası “DP”dir. Bu noktaya kadar yalnız duyulur soğutma olarak gerçekleşen soğutma prosesinin aynen devam etmesi mümkün değildir. Soğutma prosesi bu noktadan itibaren %100 doyma eğrisini takip ederek soğutma ve nem alma olarak devam ederek “EA1” noktasına kadar gelecektir. Bu proseste de dış havaya transfer olunan ısı, egzost edilen mahal havasının ısı kaybına eşittir. Bu eşitliği aşağıdaki gibi gösterebiliriz.
QOA-1 = QRA-EA1 ……………………………………………………………………………………………..…..1
QOA-1= V x cpx(1/γ) x (t1– tOA)………………………………………………………………………….2
QRA-EA1= V x cpx (1/γ)x(tRA– tDP) + V x (1/γ) x hfgx(wRA– wEA)………..……………3
QRA-EA1= V x (1/γ)x(hRA– hEA) …………………………………………………………………………4
“2” numaralı denklemdeki işlem salt ısınma işlemi olduğundan özgül ısı “cp” ve kuru termometre sıcaklık farklarını kullanarak gerçekleştirilmektedir. Ancak “3” numaralı denklem iki farklı işlemden meydana gelmektedir. Bunlardan birisi havanın duyulur olarak soğutulmasıdır. Diğeri de havadaki mutlak nem oranının azaltılmasıdır. Birinci işlem kuru termometre sıcaklık farkları ve havanın özgül ısısı dikkate alınarak gerçekleştirilmektedir. Nem alma işleminde ise mutlak nem oranında “wRA-wEA” kadar bir azalma olduğundan bu fark suyun o sıcaklıktaki buharlaşma (=yoğuşma) entalpisi ile çarpımı neticesi bulunur. Toplam ısı kaybı da bu iki değerin toplamıdır ve entalpi farklarının havanın yoğunluğu ile çarpımına eşittir.
QOA-1= V x cpx(1/γ) x (t1– tOA)
QOA-1= 10000 x 1.041 x(1/0.800) x (8 + 10)
QOA-1= 234 225 kJ/saat = 65.05 kW
QRA-EA1= V x (1/γ)x(hRA– hEA)
QRA-EA1= 10000 x (1/0.800)x(40.0 – 21.7)
QRA-EA1= 228 750 kJ/saat = 63.53 kW
Hesapları sadeleştirmek için havanın özgül hacminin sabit olduğu kabul edilmiştir. Hakikatte verilen sıcaklıklarda havanın özgül yoğunluğu 0.7467 kg/m3ile 0.8403 kg/m3arasında değişmektedir. Değerler aşağıda verilmektedir:
-10oCKT, %70rH…………………0.7467 kg/m3
+8oCKT, %20rH…………………0.7982 kg/m3
+7oCKT, %100rH…………………0.8016 kg/m3
+20oCKT, %50rH…………………0.8403 kg/m3
Egzost havası ısı kaybını hesaplarken +7oCKT ile +20oCT’deki değerlerin ortalaması ile dış havanın ısınmasında -10oCKT ile +8oCKT deki değerlerin ortalamasının kullanılmaları daha hassas bir sonuç verecektir. Ancak önerilen işlemdeki hata payı son derece düşük olduğu için uygulamalarda kullanılabilir.
Bu görüşlerin ışığı altında yapılan hesaplar neticesi egzost edilen havadan dış havaya 65 kW enerji tasarruf edilerek tasarruf sağlandığı görülmektedir. Bir de kondansasyon miktarını hesaplayalım.
M = V x (1/γ)x (wRA– wEA)
M = 10000 x (1/0.800) x( 7.7 -6.0)
M = 21 250 gram/saat
Dizayn koşullarında saatte 21.25 kg yoğuşma meydana gelecektir. Bu nedenle mahal havasının çıkış tarafına (egzost tarafına) terleme tavası konulması gerekmektedir. Eğer çıkış hızı 2.5 m/san.’in üzerindeyse ilaveten separatör (damla tutucu) konması da önerilir. Egzost havası çıkış sıcaklığı 0oC’ın üzerinde olduğu için herhangi bir şekilde karlanma riski yoktur. Eğer çıkış sıcaklığı 0oC veya daha düşük olsaydı defrost tertibatı kullanılması gerekecekti.
1.10. KARIŞIM HAVALI, DUYULUR ISI GERİ KAZANIMLI, YALNIZ ISITMALI KLİMA SANTRALI
Problem: Klima santralının toplam hava debisi 10 000 m3/saat’tir. Klima santralı %50 dış hava ile çalışmaktadır. Dış hava şartları -10oCKT, %70rH’tır. Klima santralında %60 duyulur ısı geri kazanım verimi olan plakalı eşanjör kullanılması düşünülmektedir. Mahallin ısı kaybı 30 kW’tır. Psikrometrik diyagramı çizin, ısıtıcı batarya büyüklüğünü belirleyin.
Önce psikrometrik diyagramı çizip prosesleri inceleyelim.
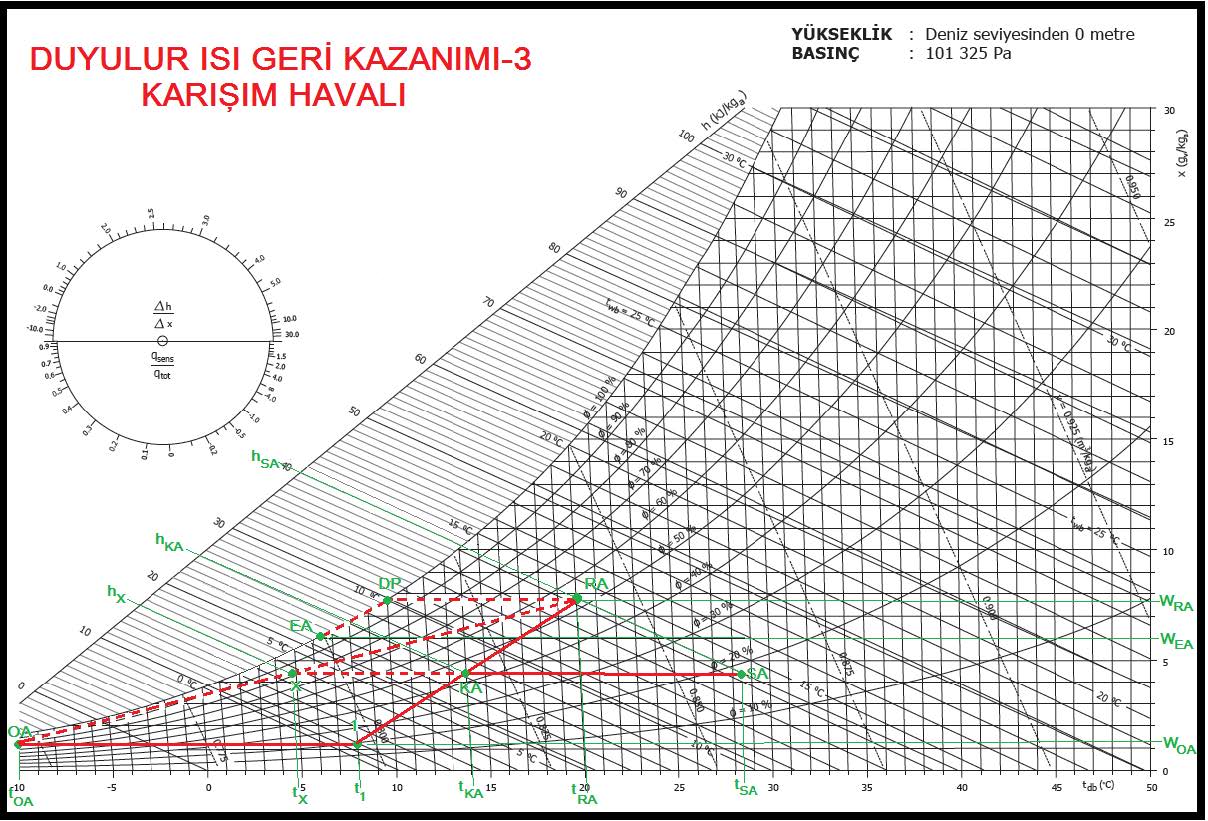
“OA” şartlarındaki dış hava palakalı ısı geri kazanım eşanjöründen geçerek “1” şartlarına kadar ısıtılma. Bu arada da “RA” şartlarında olan egzost havası “RA-DP-EA” proses hattını takip ederek soğumakta ve ısısını dış havaya transfer etmektedir. Dolayısıyla “OA-1” prosesi dış havanın ısı geri kazanımı neticesi ısınmasını göstermektedir. “1” şartlarındaki ısınmış dış hava “RA” şartlarındaki mahal havası ile %50 oranında karışarak “KA” konumunu belirler. “KA-SA” prosesi ise %50 oranında dış hava, mahal havası karışımının ısıtıcı bataryada ısıtılmasıdır. Bu prosesin 20oCKT’ye kadar olan kısmı dış havanın mahal sıcaklığına kadar ısıtılması, geri kalan kısmı ise mahal ısı kaybını karşılamak için yapılan ilave ısıtma işlemidir. Bu işleme uygun klima santralı aşağıdaki çizimde gösterilmektedir.
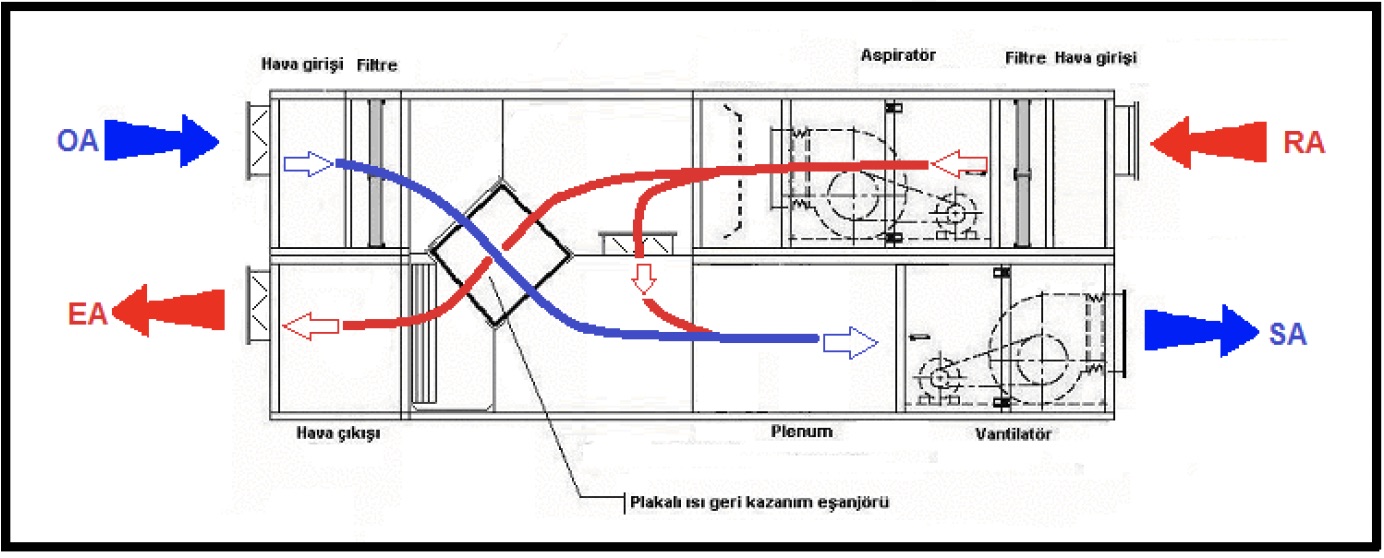
Eğer klima santralında plakalı ısı geri kazanım elemanı bulunmasaydı ısıtıcı batarya büyüklüğü “X-SA” olarak belirlenecekti. Halbuki plakalı eşanjör kullanımı ile bu büyüklük “KA-SA”ya indirgenmiş, “X-KA” kadar enerji tasarrufunda bulunulmuş bulunmaktadır.
Isı geri kazanımı olmaksızın ısıtıcı batarya büyüklüğü:
Q= V x cpx (1/γ) x ( tSA-tx)= V x (1/ϒ) x ( hSA-hx)
Isı geri kazanımı sonucu ısıtıcı batarya büyüklüğü:
Qıg= V x cpx (1/γ) x ( tSA-tKA)= V x (1/ϒ) x ( hSA-hKA)
Yapılan enerji tasarrufu ise:
ΔQ= Q – Qıg= V x cpx (1/γ) x ( tKA-tx)= V x (1/ϒ) x ( hKA-hx)
Bu ifadeleri problemimize uygularsak:
Q= 10000 x 1.041 x (1/0.825) x ( 29.4-5)=295 757 kJ/saat =82.14 kW
Qıg= 10000 x 1.041 x (1/0.825) x ( 29.4-14)=194 320 kJ/saat= 53.97 kW….. ısıtıcı batarya büyüklüğü ve;
ΔQ= Q – Qıg= 82.14 – 53.97 = 28.17 kW…………enerji tasarrufu bulunur.
1.11. %100 DIŞ HAVALI, TOPLAM ENERJİ GERİ KAZANIMLI, YALNIZ ISITMALI KLİMA SANTRALI
Çözümlü örneklere geçmeden önce, toplam ısı geri kazanımlı eşanjörler hakkında kısa bilgi verelim. 1.8 sayılı konumuzda ısı geri kazanım elemanlarının genel tanımını yapmış, dört değişik tip elemanı incelemiştik. Bunlardan ikisinin entalpi bazında ısı geri kazanımı yapabildiğini görmüştük. Entalpi bazında ısı geri kazanımı hem duyulur ısı geri kazanımını, hem de gizli ısı geri kazanımı içerir. Bu nedenle bu tip eşanjörler için iki değişik verim kullanılır.
ηduy=100 x (tRA-tEA)/(tRA-tOA)
ηgiz= 100 x (wRA-wEA)/(wRA-wOA)
Bu formülde:
ηduy= Eşanjörün duyulur ısı kazanım verimi……………………………………………. (%)
tRA= Egzost edilen havanın eşanjöre giriş sıcaklığı …………………………….…..(oC)
tEA= Egzost edilen havanın eşanjörden çıkış sıcaklığı ……………….…………….(oC)
tOA= Dış hava sıcaklığı…………………………………………………………………….…………(oC)
ηgiz= Eşanjörün gizli ısı kazanım verimi…………………..………………………………. (%)
wRA= Egzost edilen havanın mutlak nem oranı …………………….…….…..( gr/kgda)
wEA= Egzost edilen havanın eşanjörden çıkış mutlak nem oranı ..….( gr/kgda)
wOA= Dış havanın mutlak nem oranı…………………………………….……………(gr/kgda)
Bu işlemi entalpi tekerleği de tabir edilen döner tamburlu toplam enerji geri kazanım elemanını inceleyerek yapalım.
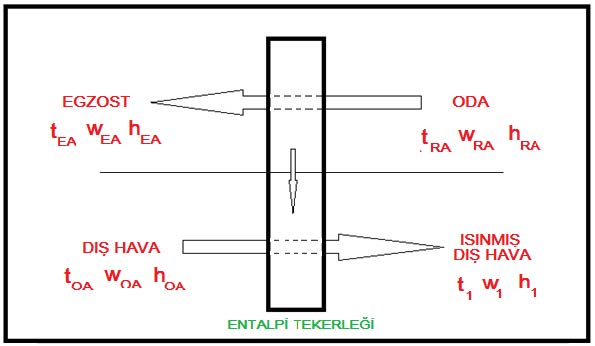
Şematik çizimdeki semboller şöyledir.
tRA= Egzost edilen havanın eşanjöre giriş sıcaklığı …………………………………..(oC)
wRA= Egzost edilen havanın mutlak nem oranı ……………………………….( gr/kgda)
hRA= Egzost edilen havanın entalpisi ……………..…………………………………..( kJ/kg)
tEA= Egzost edilen havanın eşanjörden çıkış sıcaklığı ………………………………(oC)
wEA= Egzost edilen havanın eşanjörden çıkış mutlak nem oranı ……( gr/kgda)
hEA= Egzost edilen havanın eşanjörden çıkış entalpisi ……………..……….( kJ/kg)
tOA= Dış havanın eşanjöre giriş sıcaklığı ………………………..…………………………(oC)
wOA= Dış havanın mutlak nem oranı …………………………..………………..….( gr/kgda)
hOA= Dış havanın entalpisi ……………..………………………..………………………….( kJ/kg)
t1 = Dış havanın eşanjörden çıkış sıcaklığı ………………………..………………………(oC)
w1 = Dış havanın eşanjörden çıkış mutlak nem oranı ……………..……….( gr/kgda)
h1 = Dış havanın eşanjörden çıkış entalpisi ……………..………………………….( kJ/kg)
Hava yoğunluğunun sıcaklığa bağlı olarak çok az değişeceği nedeniyle sabit kabul edilmesi durumunda verim formüllerimiz aşağıdaki duruma gelir.
ηduy=100 x (tRA-tEA)/(tRA-tOA)= 100 x (t1-tOA)/(tRA-tOA)
ηgiz= 100 x (wRA-wEA)/(wRA-wOA) = 100 x (w1-wOA)/(wRA-wOA)
ηtop= 100 x (hRA-hEA)/(hRA-hOA) = 100 x (h1-hOA)/(hRA-hOA)
Şimdi yukarıdaki işlemleri bir örnekle hesaplayalım ve psikrometrik diyagramda prosesi gösterelim.
Problem: Klima santralının toplam hava debisi 10 000 m3/saat’tir. Klima santralı %100 dış hava ile çalışmaktadır.Mahal şartları 20oCKT, %50 rH, dış hava şartları ise -10oCKT, %70rH’tır. Klima santralında %75 duyulur ısı geri kazanım verimi, %55 gizli ısı geri kazanım verimi olan entalpi tekerleği kullanılmaktadır. Egzost havası ile dış havanın eşanjör çıkış şartlarını ve sistemin toplam ısı geri kazanım verimini hesaplayın.
ηduy=100 x (tRA-tEA)/(tRA-tOA)= 100 x (t1-tOA)/(tRA-tOA)
75 =100 x (20-tEA)/(20 + 10)
TEA= -2.5oCKT
ηduy= 100 x (t1-tOA)/(tRA-tOA)
ηduy= 100 x (t1-tOA)/(tRA-tOA)
75 = 100 x (t1+10)/(20 + 10)
t1= +12.5oCKT
ηgiz= 100 x (wRA-wEA)/(wRA-wOA)
55 = 100 x (7.2 -wEA)/(7.2 – 1.3)
wEA= 3.95 gr/kgda
ηgiz= 100 x (w1-wOA)/(wRA-wOA)
55 = 100 x (w1 – 1.3)/(7.2 – 1.3)
w1 = 5.25 gr/kgda
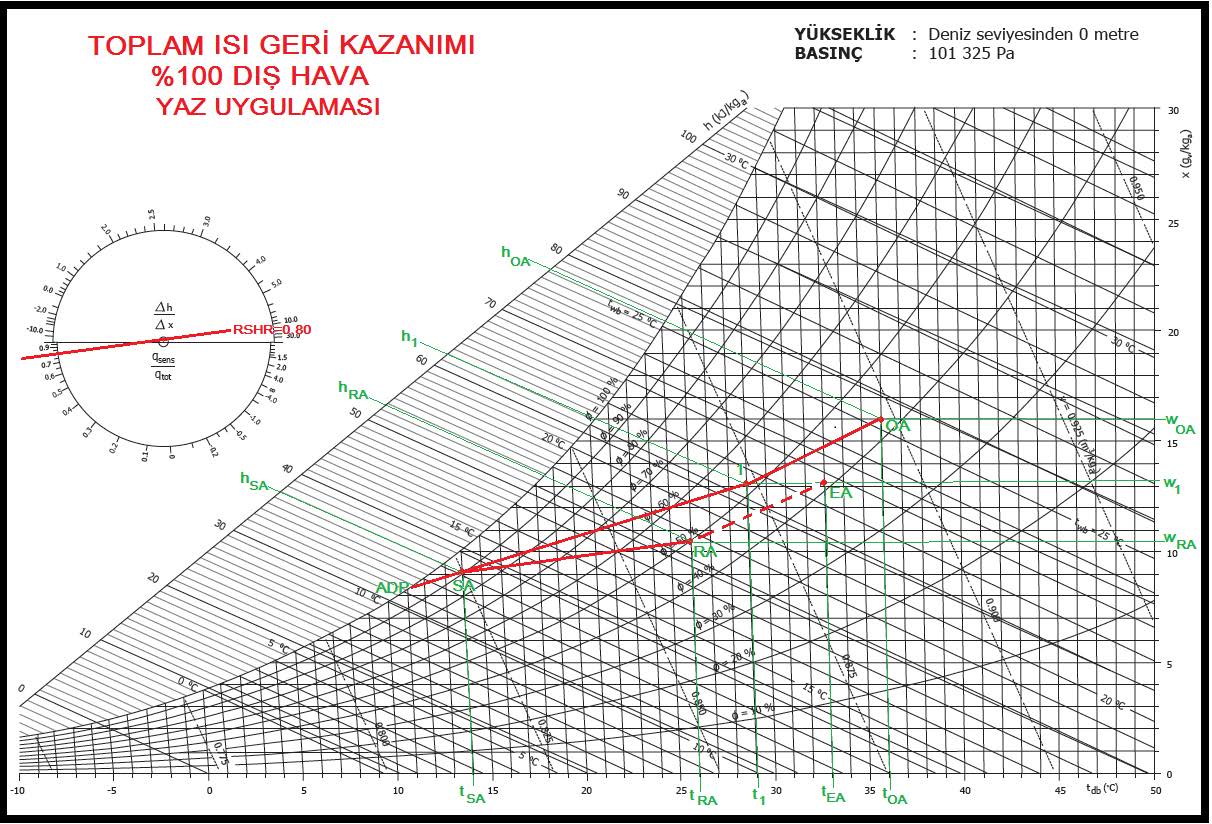
Bu değerleri psikrometrik diyagram üzerine koyup “OA-1” ve “RA-EA” proses doğrularını çizelim.
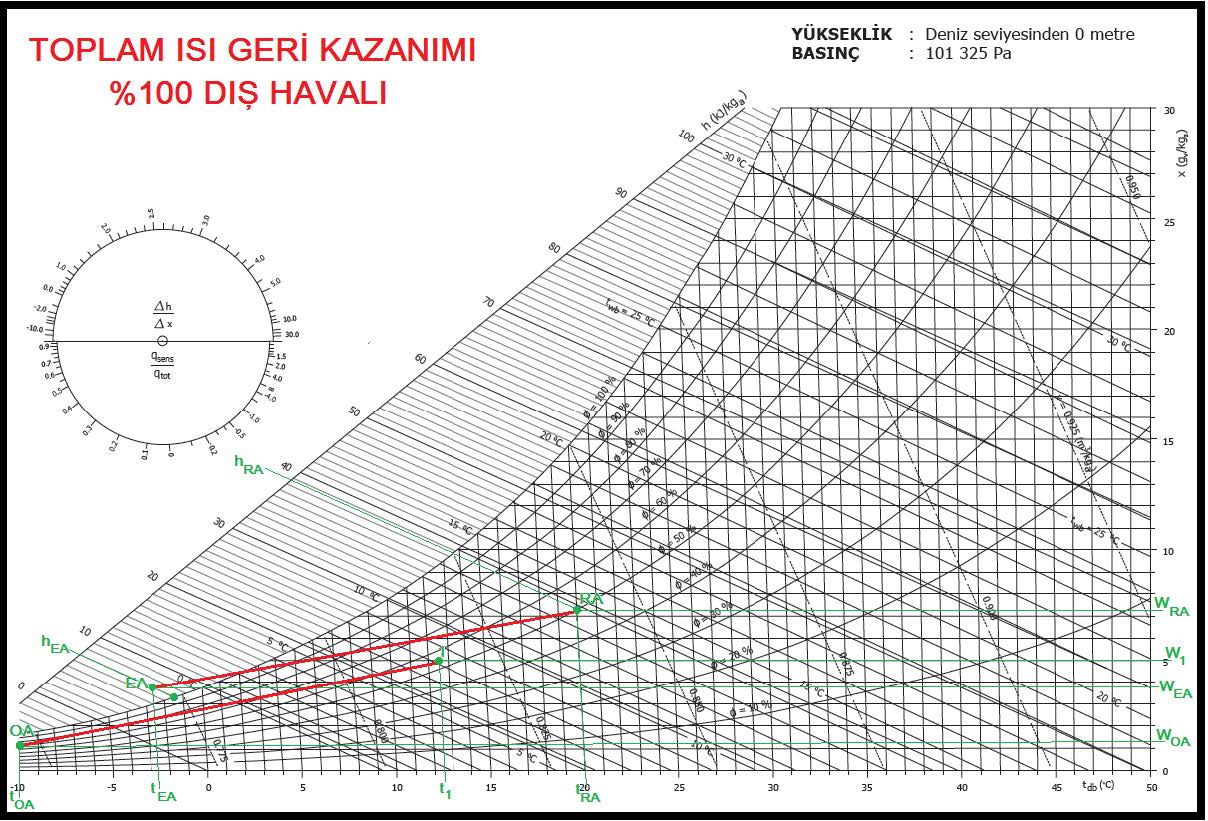
Şimdi de sistemin toplam ısı geri kazanım verimini hesaplayalım.
ηtop= 100 x (hRA-hEA)/(hRA-hOA)
hRA= 38.8 kJ/kg
hEA= 7.0 kJ/kg
hOA= -7.2585 kJ/kg (bkz. Psikrometri-I, sayfa-132, Tablo-8)
ηtop= 100 x (38.8 – 7.0)/(38.8 + 7.2585)
ηtop= 69 (%)
Uygulamamızda sistemin toplam enerji bazında ısı geri kazanım verimi %69’dur.
1.12. KARIŞIM HAVALI, TOPLAM ENERJİ GERİ KAZANIMLI, YALNIZ ISITMALI KLİMA SANTRALI
Problem: Klima santralının toplam hava debisi 10 000 m3/saat’tir. Klima santralı %50 dış hava ile çalışmaktadır.Mahal şartları 22oCKT, %50 rH, dış hava şartları ise -5oCKT, %70rH’tır. Klima santralında %75 duyulur ısı geri kazanım verimi, %45 gizli ısı geri kazanım verimi olan entalpi tekerleği kullanılmaktadır. Mahal ısı kaybı 30 kW’tır. Egzost havası ile dış havanın eşanjör çıkış şartlarını ve sistemin toplam ısı geri kazanım verimini hesaplayın.
Qmahal= 30 kW= 30 x 3600.65 = 108 110 kJ/saat
Qmahal=V x cpx (1/γ)x (tSA – t1)
108 110 = 10 000 x 1.041 x (1/0.85) x (tSA – 20)
tSA = 28.82oC
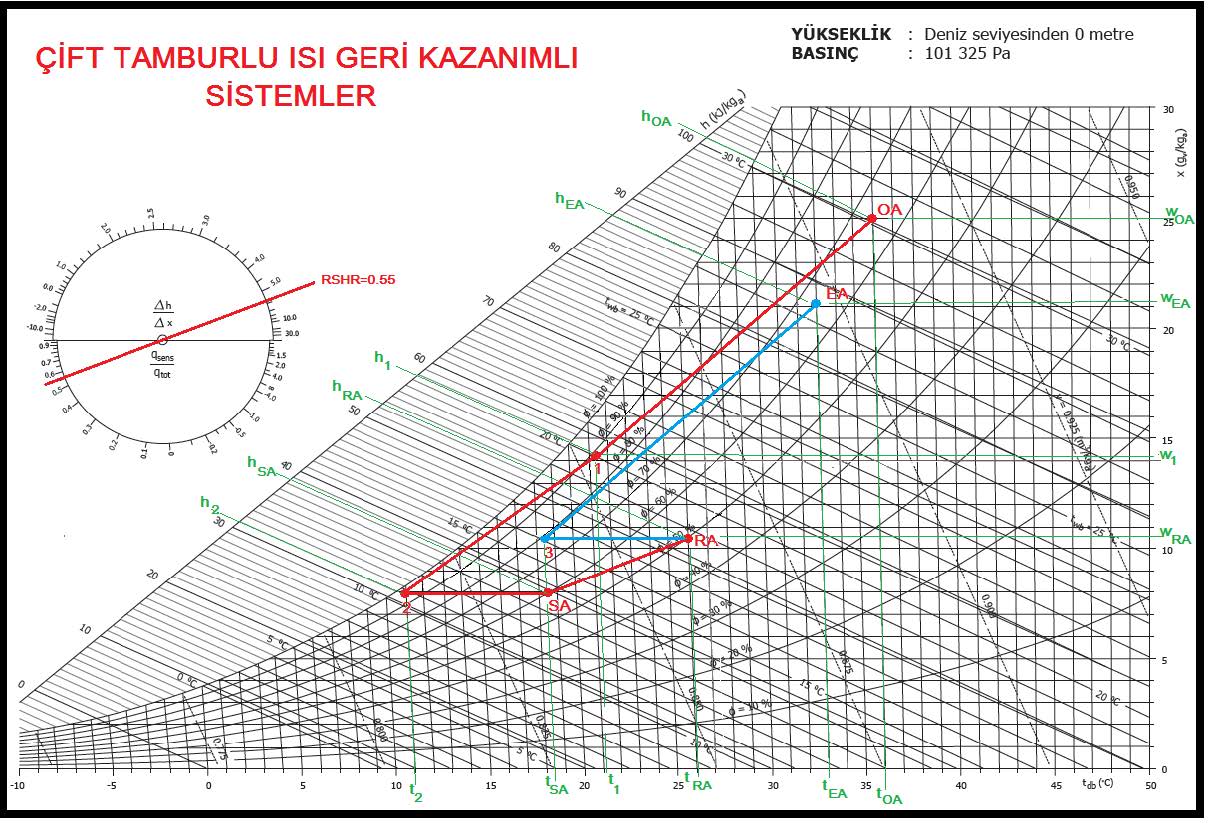
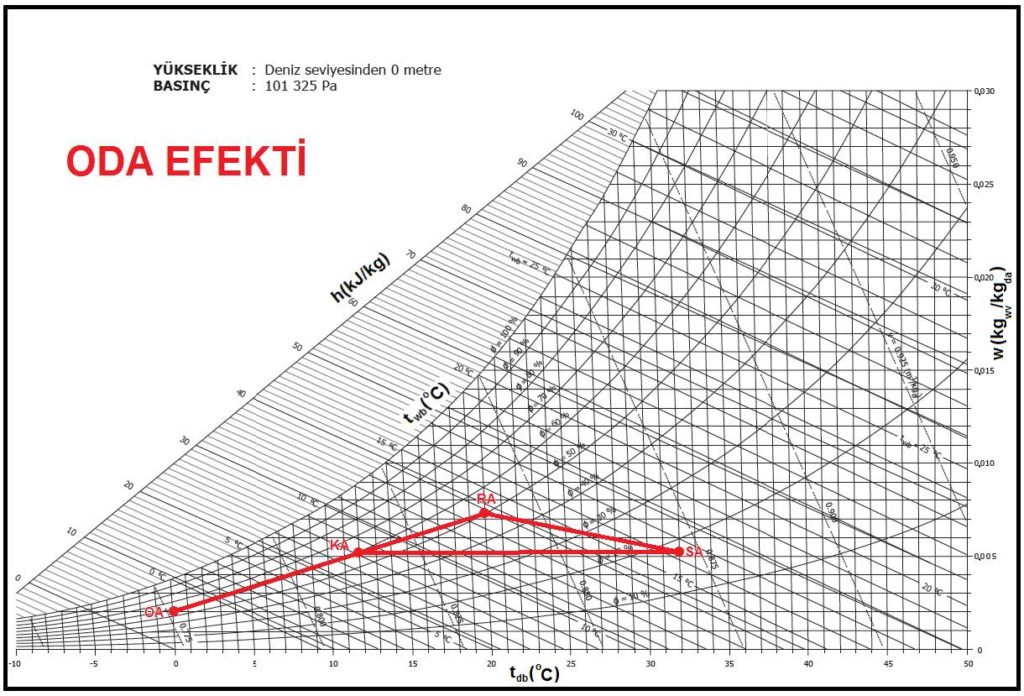
Şimdi prosesi psikrometrik diyagramda gösterelim.
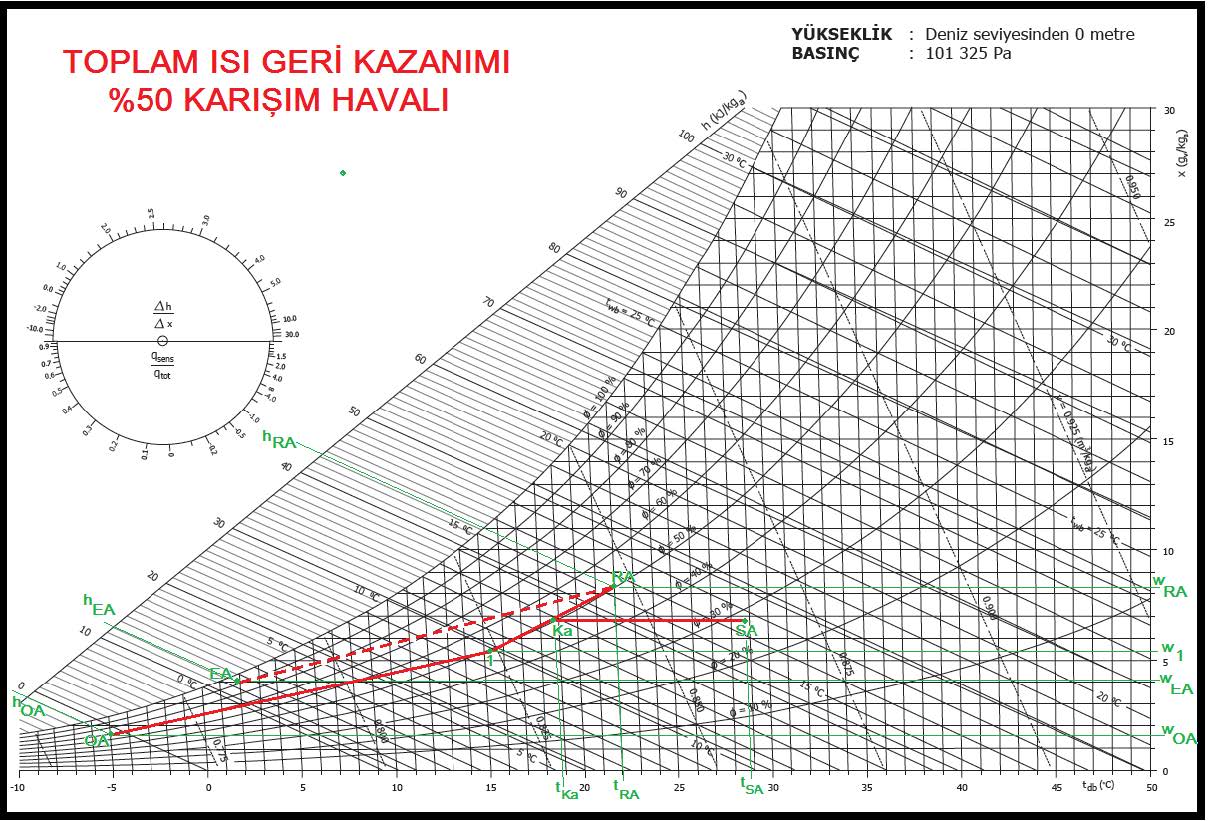
Psikrometrik diyagramımızda “OA-1” hattı, döner tamburda dış havanın ısı ve kütle transferi neticesi kuru termometre sıcaklığıyla mutlak nem oranının artarak “OA” konumunan “1” konumuna gelmesi prosesidir. Kesik çizgiyle gösterilen “RA-EA” hattı aynı döner tamburda, egzost edilen hava içindeki duyulur ısı ile mutlak nem oranının dış havaya transferidir. “1-RA” hattı, döner tamburdan “1” şartlarında çıkan dış hava ile “RA” şartlarındaki oda havasının karışım prosesidir. “Ka” karışım havasının konumunu bu hat üzerinde karışım yüzdesi belirler. “Ka-SA” ise karışım havasının sevk şartı olan “SA” konumuna kadar ısıtıcı bataryada ısıtılmasıdır. Havanın “tKa” kuru termometre sıcaklığından “tRA” kuru termometre sıcaklığına ısıtılması, karışım havasının mahal şartlarına kadar ısıtılmasıdır. “tRA”dan “tSA” kuru termometre sıcaklığına ısıtılması ise mahal ısı kaybını karşılamak içindir.
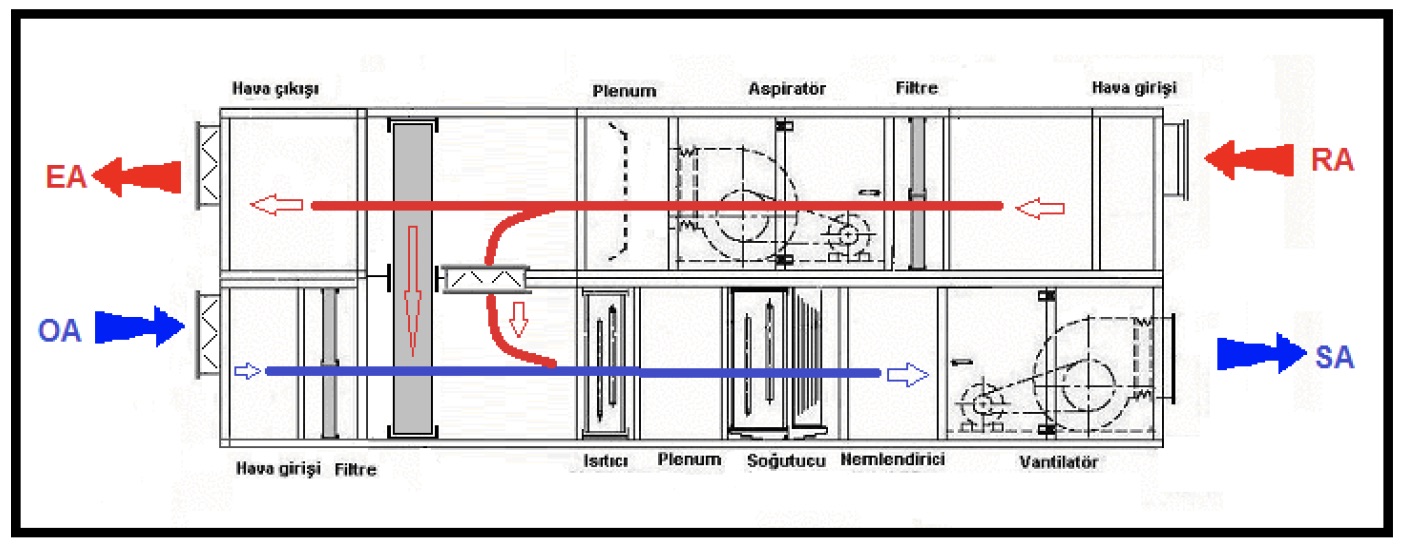
Bu prosese uygun klima santralı yukarıda görülmektedir. Klima santralı içinde soğutucu batarya da bulunmaktadır. Ancak soğutma ile ilgili prosesleri “Yaz Kliması” isimli bahiste inceleyeceğiz.
Isıtıcı batarya kapasitesinin belirlenmesi
ΣQ = V x cp x (1/γ) x ( tSA – tKa)
ΣQ = 10 000 x 1.041 x (1/0.85) x (28.82– 18.80)
ΣQ = 122 716 kJ/saat
ΣQ = 34.08 kW
Bu kapasitenin 4.08 kW’ı karışım havasının mahal şartlarına kadar ısıtılması için gerekli olan kapasitedir.
ΣQ = QKa + Qmahal
QKa= V x cp x (1/γ) x ( tRA – tKa)
QKa= 10 000 x 1.041x (1/0.85) x ( 20– 18.80 )
QKa= 14 696 kJ/saat = 4.08 kW
Mahal ısı kaybı
30 kW= 30 x 3600.65 = 108 110 kJ/saat
Qmahal=V x cpx (1/γ)x (tSA – tRA)
108 110 = 10 000 x 1.041 x (1/0.85) x (tSA – 22)
tSA = 30.82oC
Bu arada sistemimizin toplam ısı geri kazanım verimliliğini hesaplayalım.
η= (hRA– hEA)/(hRA– hOA)
hRA= 43.3 kJ/kg
hEA = 12.1 kJ/kg
hOA = -1.0 kJ/kg
η= (43.3 – 12.1)/(43.3 + 1.0)
η= 0.70 = %70
geri kazanılan ısı miktarı ise:
Qhr= Vdışhavax (1/γ) x (hRA– hEA )
Qhr= (10 000 x 0.50) x (1/0.825) x (43.3- 12.1)
Qhr= 189090 kJ/saat = 52.53 kW

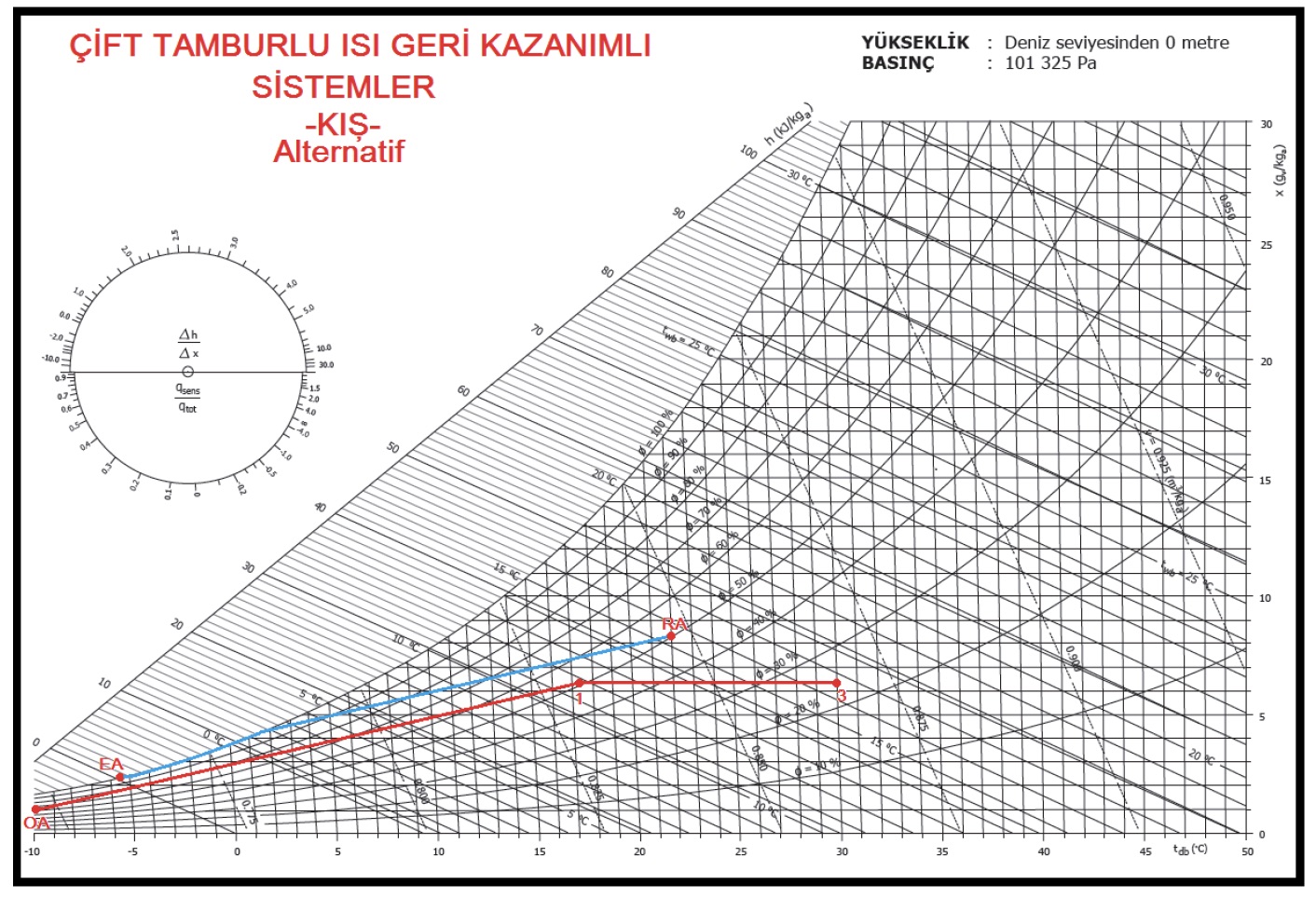
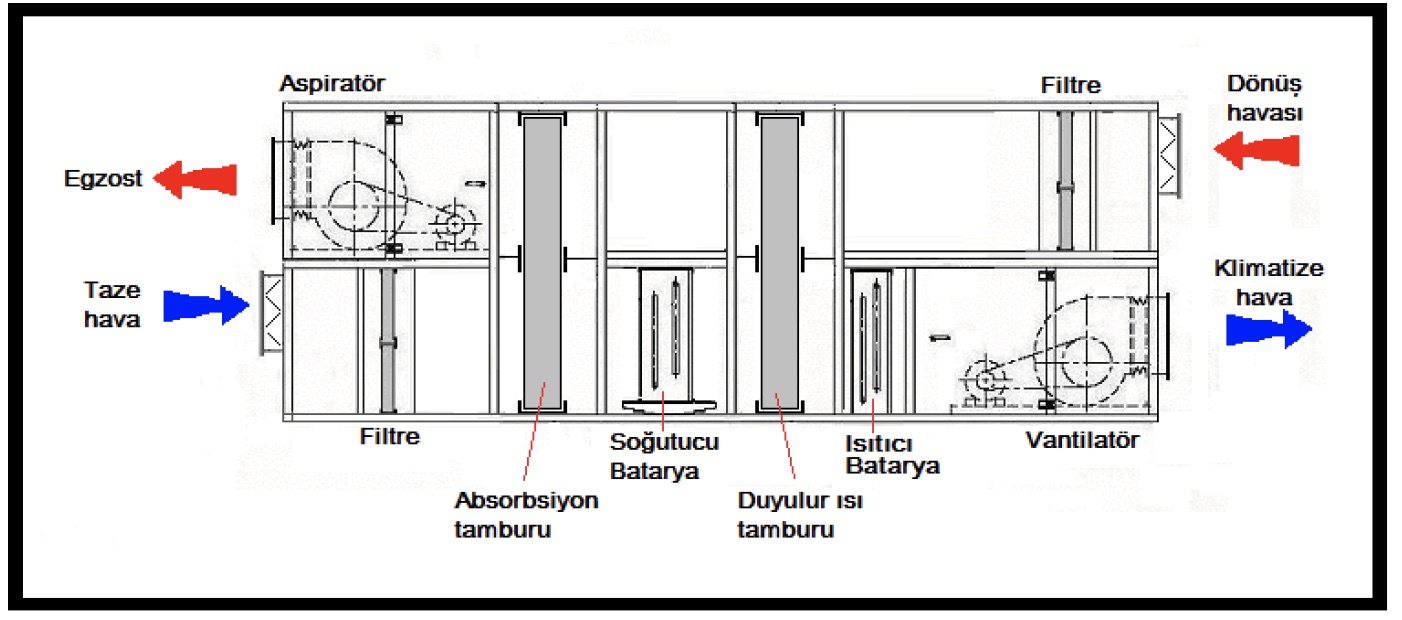
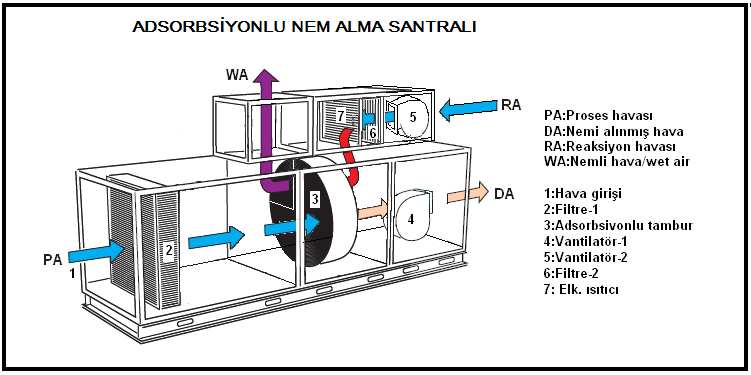
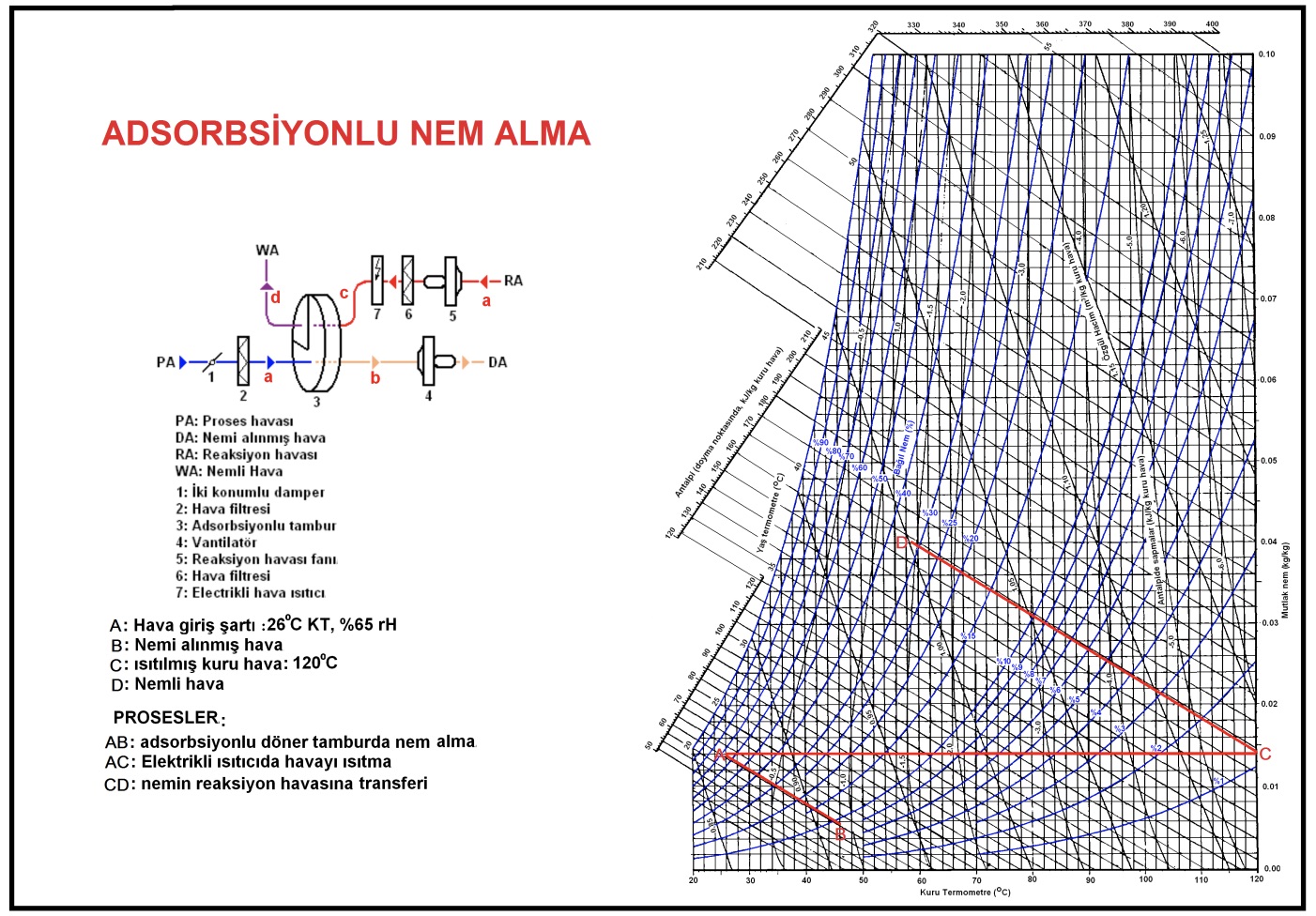
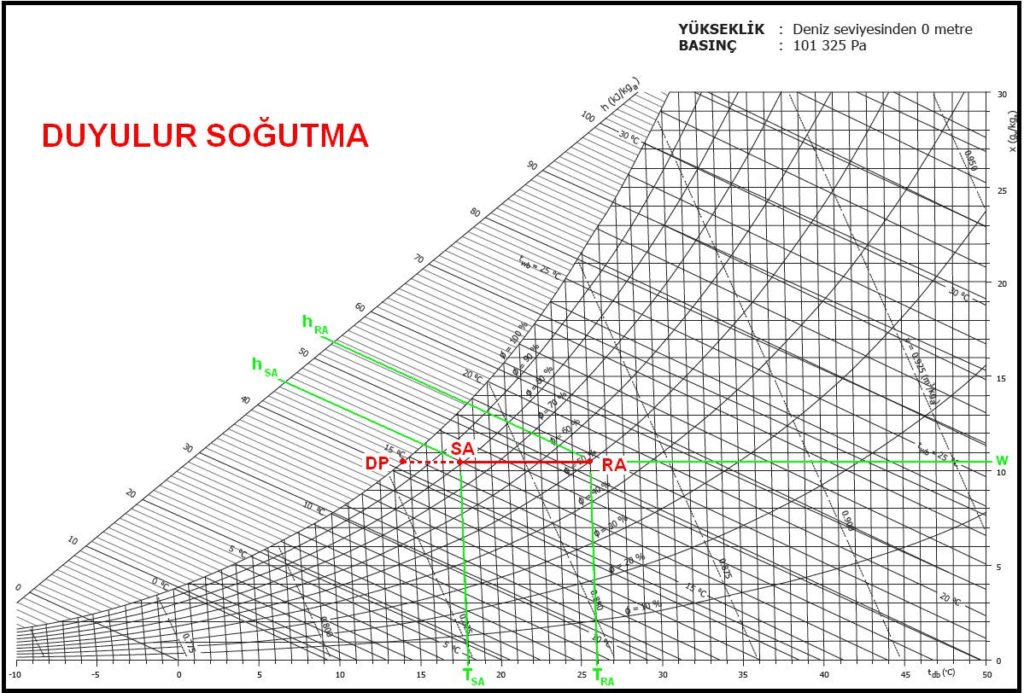
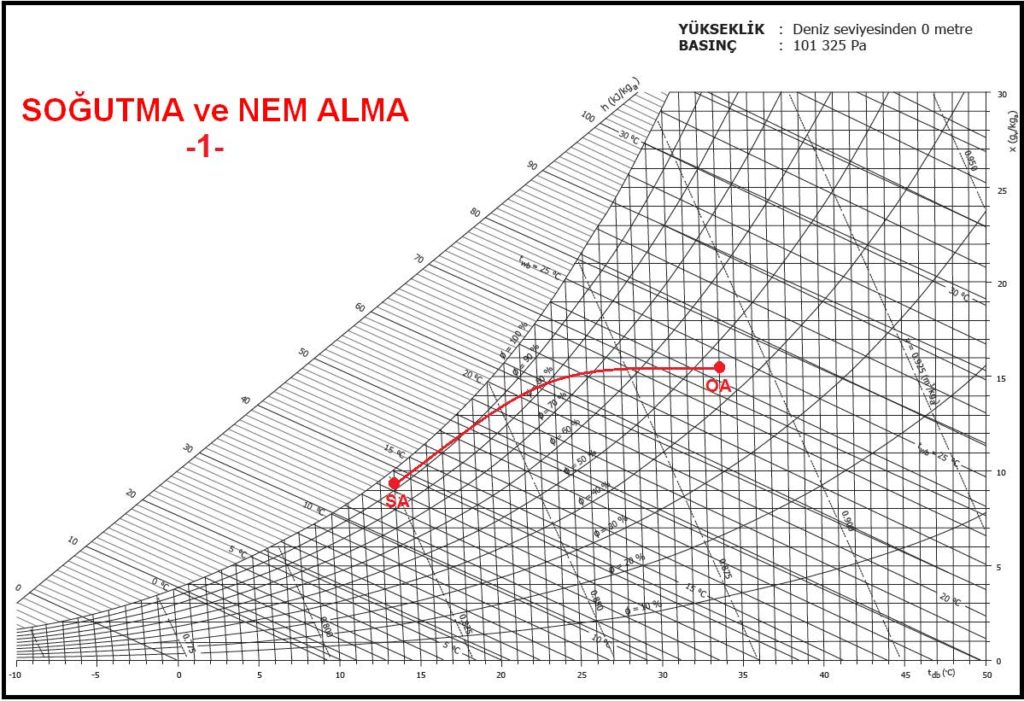
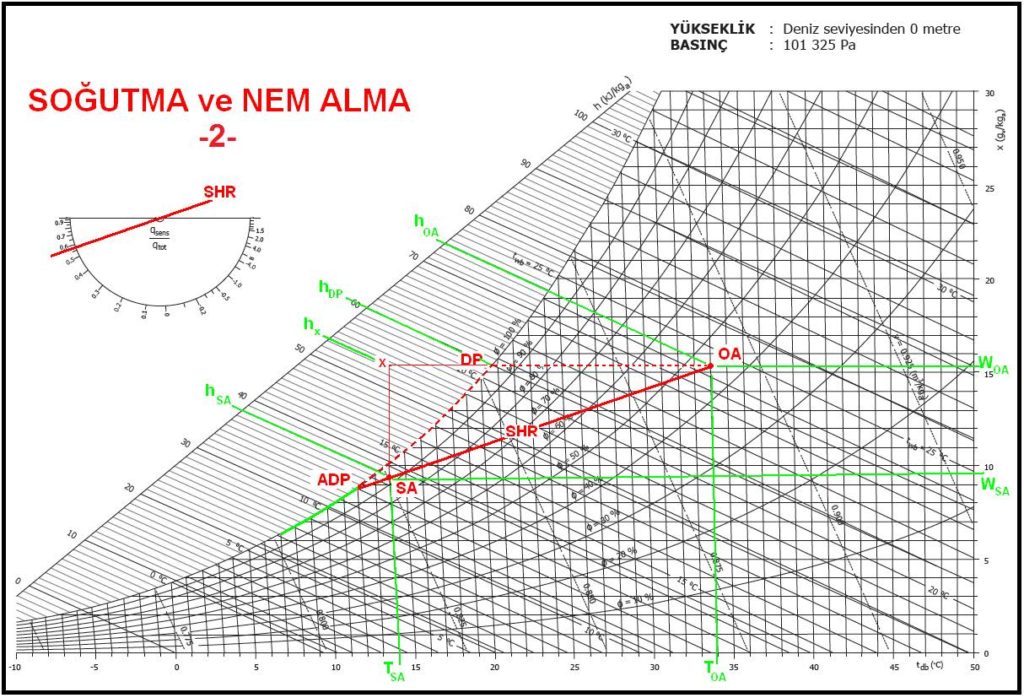





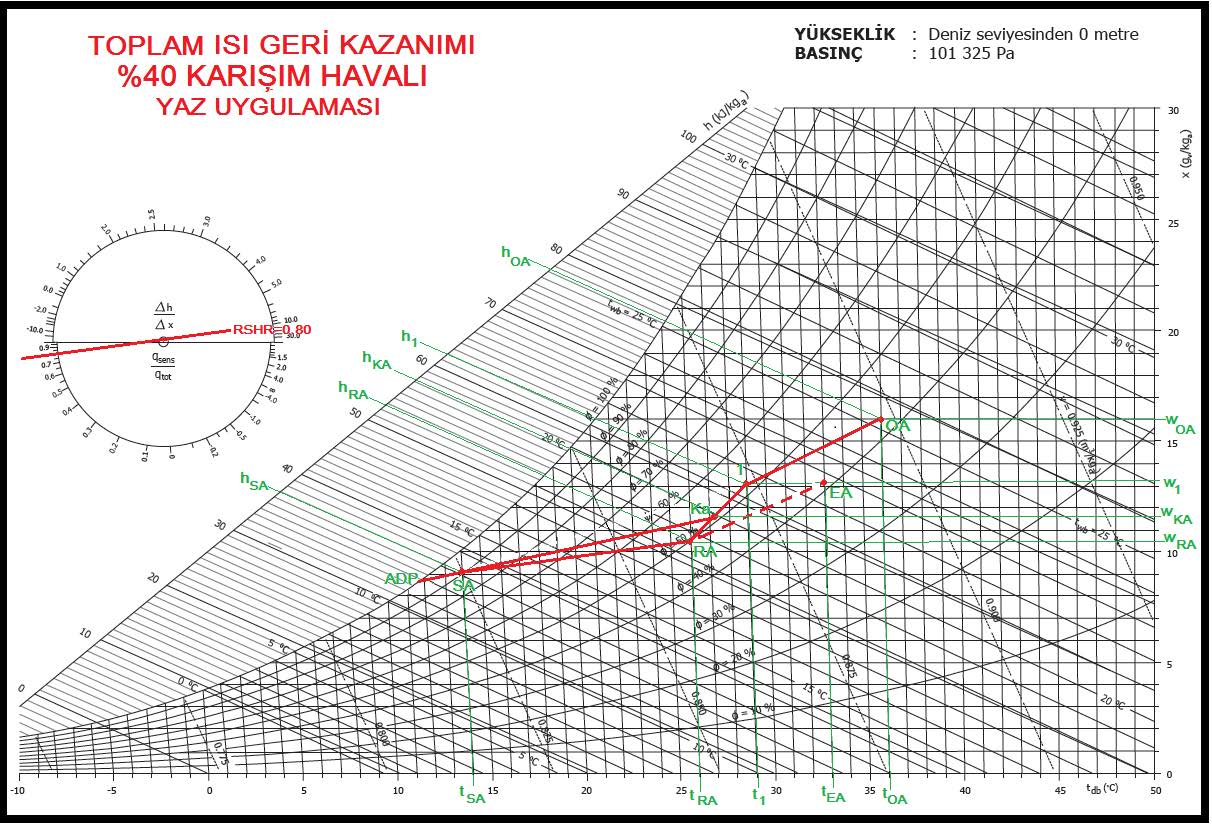
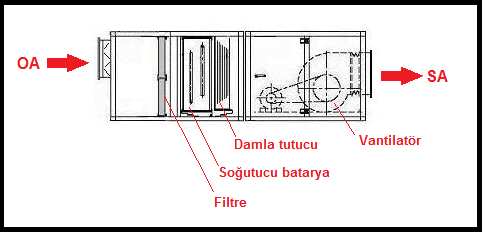 2.3. KARIŞIM HAVALI KLİMA SANTRALI, YALNIZ SOĞUTMA
2.3. KARIŞIM HAVALI KLİMA SANTRALI, YALNIZ SOĞUTMA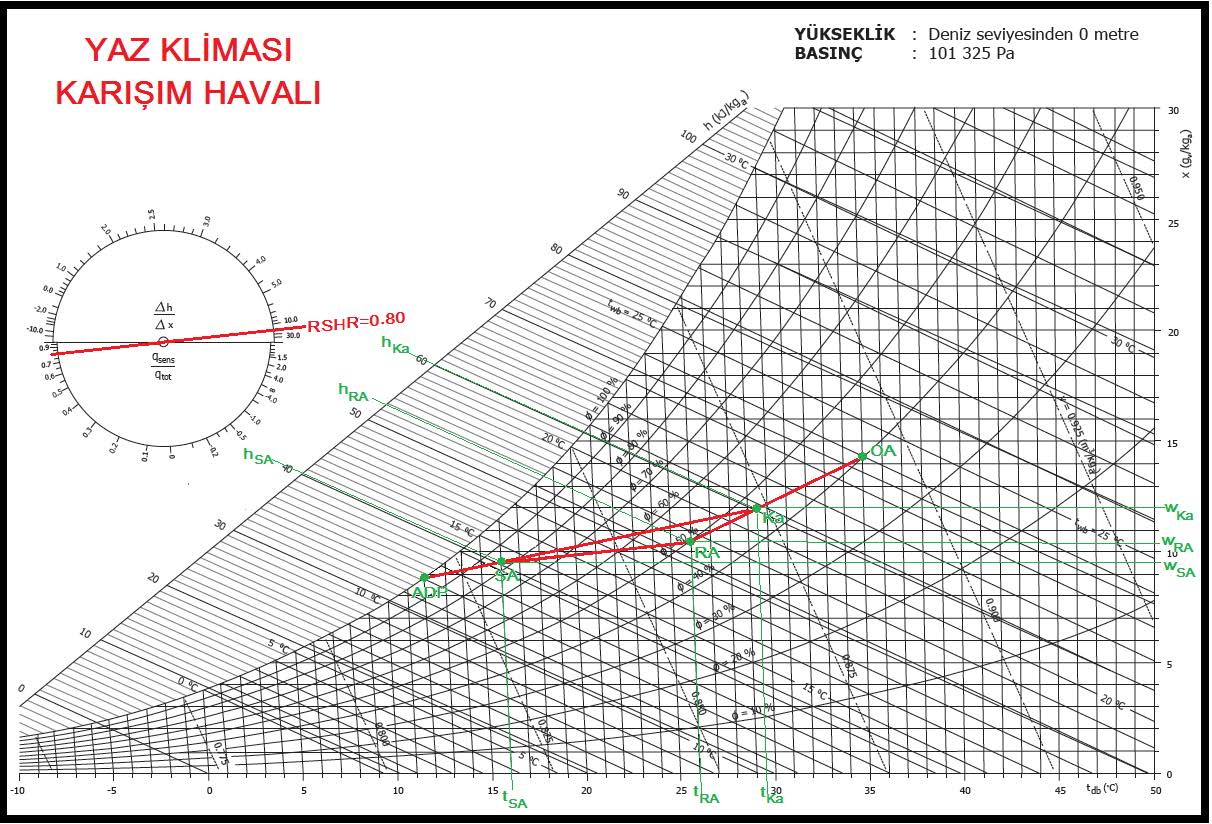
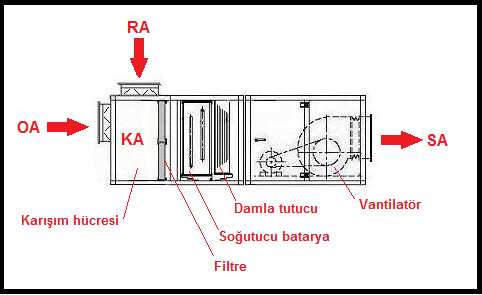
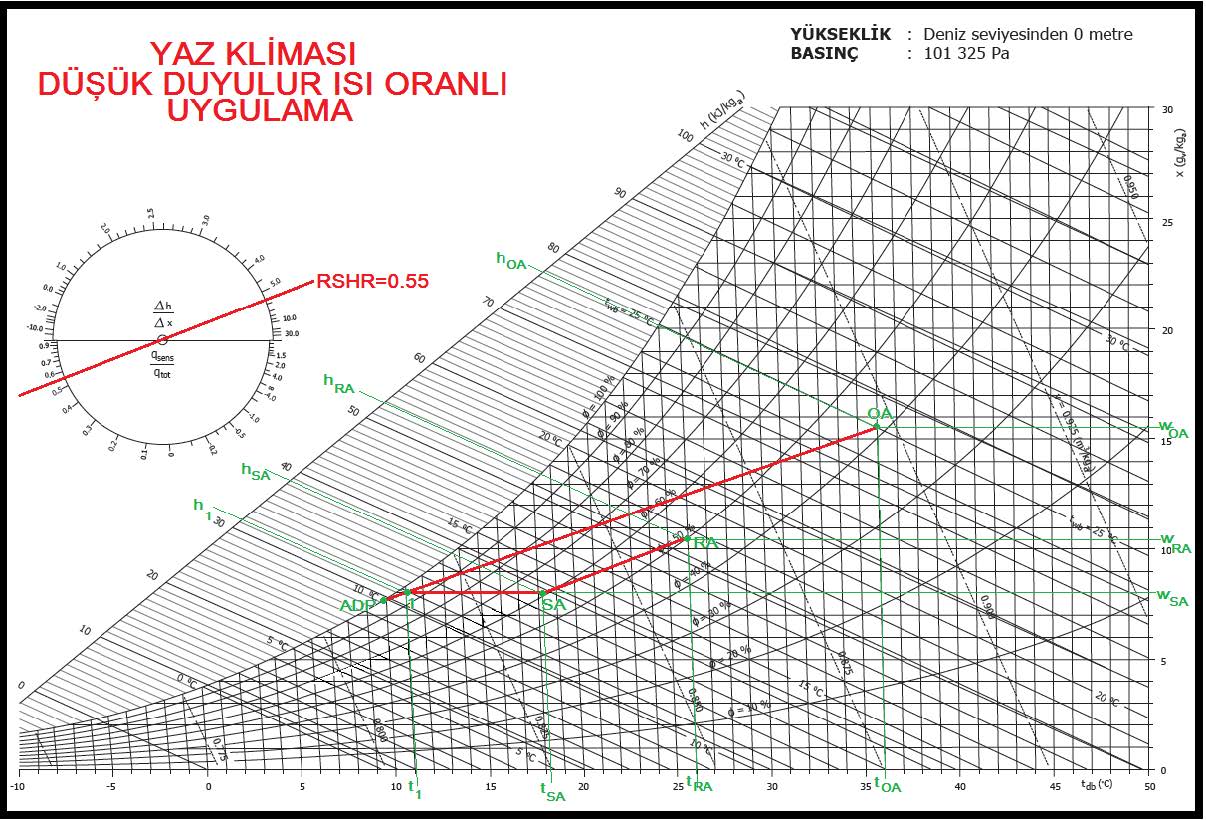
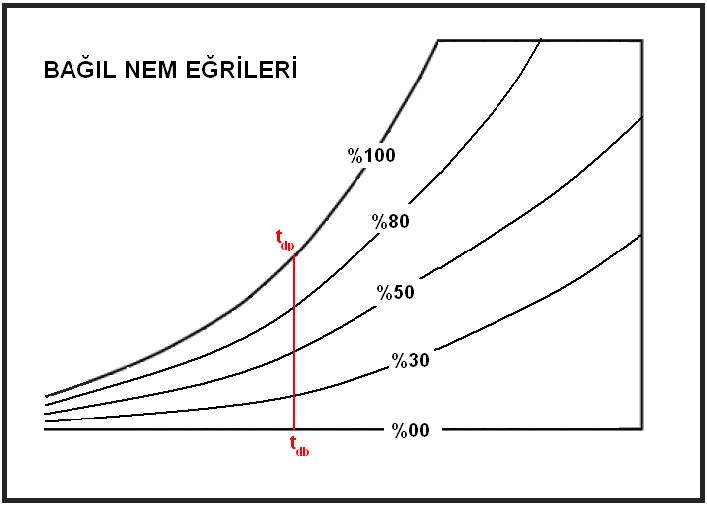
 3.2. Kuru Termometre Sıcaklığı
3.2. Kuru Termometre Sıcaklığı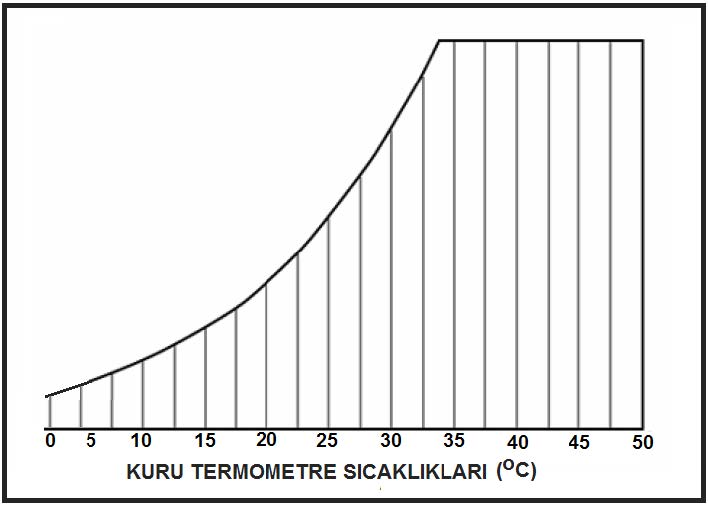
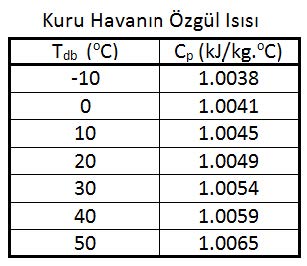
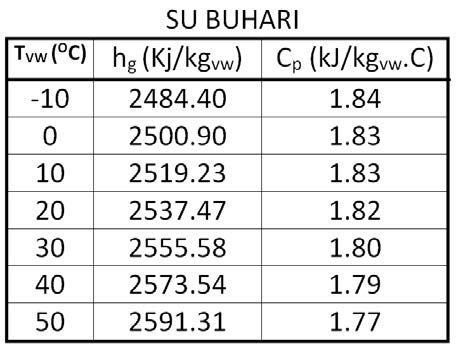

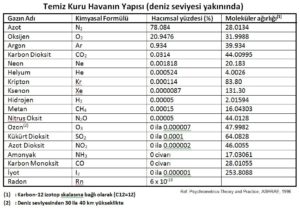
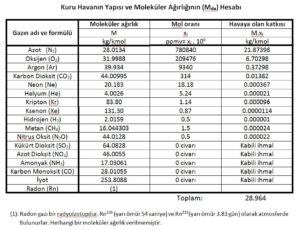
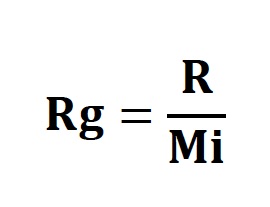 Bu duruma göre azot, oksijen ve kuru havanın gaz sabitleri şu şekilde bulunur:
Bu duruma göre azot, oksijen ve kuru havanın gaz sabitleri şu şekilde bulunur: